Reconstructing classes of 3D FRI signals from sampled tomographic projections at unknown angles

Traditional sampling schemes often assume that the sampling locations are known. Motivated by the recent bioimaging technique known as cryogenic electron microscopy (cryoEM), we consider the problem of reconstructing an unknown 3D structure from samples of its 2D tomographic projections at unknown angles. We focus on 3D convex bilevel polyhedra and 3D point sources and show that the exact estimation of these 3D structures and of the projection angles can be achieved up to an orthogonal transformation. Moreover, we are able to show that the minimum number of projections needed to achieve perfect reconstruction is independent of the complexity of the signal model. By using the divergence theorem, we are able to retrieve the projected vertices of the polyhedron from the sampled tomographic projections, and then we show how to retrieve the 3D object and the projection angles from this information. The proof of our theorem is constructive and leads to a robust reconstruction algorithm, which we validate under various conditions. Finally, we apply aspects of the proposed framework to calibration of X-ray computed tomography (CT) data.

Empowering Networks With Scale and Rotation Equivariance Using A Similarity Convolution

The translational equivariant nature of Convolutional Neural Networks (CNNs) is a reason for its great success in computer vision. However, networks do not enjoy more general equivariance properties such as rotation or scaling, ultimately limiting their generalization performance. To address this limitation, we devise a method that endows CNNs with simultaneous equivariance with respect to translation, rotation, and scaling. Our approach defines a convolution-like operation and ensures equivariance based on our proposed scalable Fourier-Argand representation. The method maintains similar efficiency as a traditional network and hardly introduces any additional learnable parameters, since it does not face the computational issue that often occurs in group-convolution operators. We validate the efficacy of our approach in the image classification task, demonstrating its robustness and the generalization ability to both scaled and rotated inputs.

Denoising of Three-Dimensional Fast Spin Echo Magnetic Resonance Images of Knee Joints using Spatial-Variant Noise-Relevant Residual Learning of Convolution Neural Network

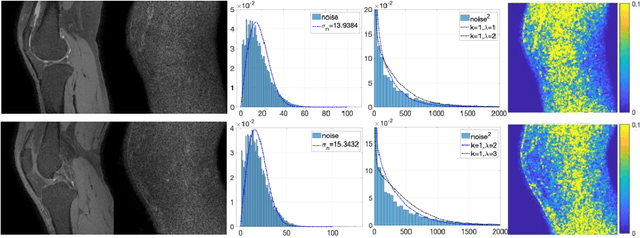
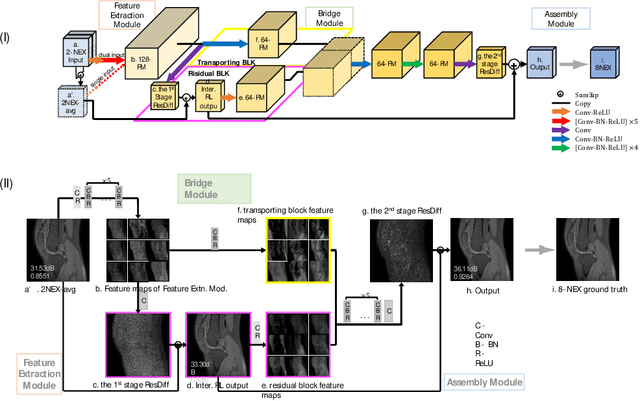
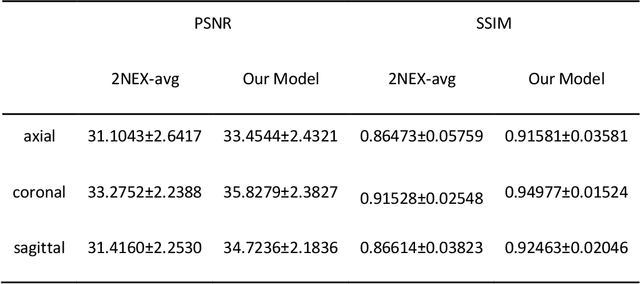
Two-dimensional (2D) fast spin echo (FSE) techniques play a central role in the clinical magnetic resonance imaging (MRI) of knee joints. Moreover, three-dimensional (3D) FSE provides high-isotropic-resolution magnetic resonance (MR) images of knee joints, but it has a reduced signal-to-noise ratio compared to 2D FSE. Deep-learning denoising methods are a promising approach for denoising MR images, but they are often trained using synthetic noise due to challenges in obtaining true noise distributions for MR images. In this study, inherent true noise information from 2-NEX acquisition was used to develop a deep-learning model based on residual learning of convolutional neural network (CNN), and this model was used to suppress the noise in 3D FSE MR images of knee joints. The proposed CNN used two-step residual learning over parallel transporting and residual blocks and was designed to comprehensively learn real noise features from 2-NEX training data. The results of an ablation study validated the network design. The new method achieved improved denoising performance of 3D FSE knee MR images compared with current state-of-the-art methods, based on the peak signal-to-noise ratio and structural similarity index measure. The improved image quality after denoising using the new method was verified by radiological evaluation. A deep CNN using the inherent spatial-varying noise information in 2-NEX acquisitions was developed. This method showed promise for clinical MRI assessments of the knee, and has potential applications for the assessment of other anatomical structures.

LAPNet: Non-rigid Registration derived in k-space for Magnetic Resonance Imaging

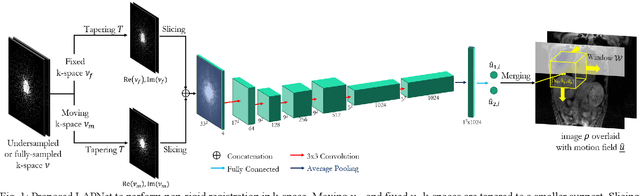
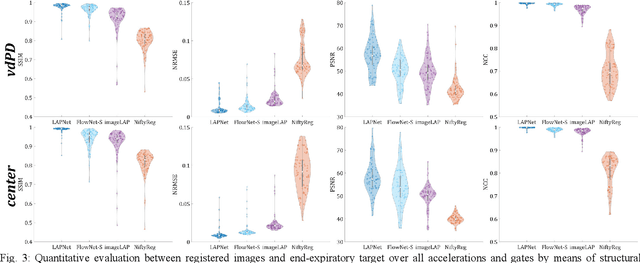
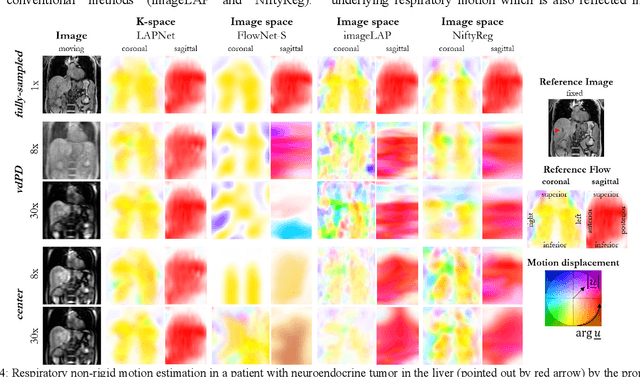
Physiological motion, such as cardiac and respiratory motion, during Magnetic Resonance (MR) image acquisition can cause image artifacts. Motion correction techniques have been proposed to compensate for these types of motion during thoracic scans, relying on accurate motion estimation from undersampled motion-resolved reconstruction. A particular interest and challenge lie in the derivation of reliable non-rigid motion fields from the undersampled motion-resolved data. Motion estimation is usually formulated in image space via diffusion, parametric-spline, or optical flow methods. However, image-based registration can be impaired by remaining aliasing artifacts due to the undersampled motion-resolved reconstruction. In this work, we describe a formalism to perform non-rigid registration directly in the sampled Fourier space, i.e. k-space. We propose a deep-learning based approach to perform fast and accurate non-rigid registration from the undersampled k-space data. The basic working principle originates from the Local All-Pass (LAP) technique, a recently introduced optical flow-based registration. The proposed LAPNet is compared against traditional and deep learning image-based registrations and tested on fully-sampled and highly-accelerated (with two undersampling strategies) 3D respiratory motion-resolved MR images in a cohort of 40 patients with suspected liver or lung metastases and 25 healthy subjects. The proposed LAPNet provided consistent and superior performance to image-based approaches throughout different sampling trajectories and acceleration factors.