scASDC: Attention Enhanced Structural Deep Clustering for Single-cell RNA-seq Data

Single-cell RNA sequencing (scRNA-seq) data analysis is pivotal for understanding cellular heterogeneity. However, the high sparsity and complex noise patterns inherent in scRNA-seq data present significant challenges for traditional clustering methods. To address these issues, we propose a deep clustering method, Attention-Enhanced Structural Deep Embedding Graph Clustering (scASDC), which integrates multiple advanced modules to improve clustering accuracy and robustness.Our approach employs a multi-layer graph convolutional network (GCN) to capture high-order structural relationships between cells, termed as the graph autoencoder module. To mitigate the oversmoothing issue in GCNs, we introduce a ZINB-based autoencoder module that extracts content information from the data and learns latent representations of gene expression. These modules are further integrated through an attention fusion mechanism, ensuring effective combination of gene expression and structural information at each layer of the GCN. Additionally, a self-supervised learning module is incorporated to enhance the robustness of the learned embeddings. Extensive experiments demonstrate that scASDC outperforms existing state-of-the-art methods, providing a robust and effective solution for single-cell clustering tasks. Our method paves the way for more accurate and meaningful analysis of single-cell RNA sequencing data, contributing to better understanding of cellular heterogeneity and biological processes. All code and public datasets used in this paper are available at \url{https://github.com/wenwenmin/scASDC} and \url{https://zenodo.org/records/12814320}.

stMCDI: Masked Conditional Diffusion Model with Graph Neural Network for Spatial Transcriptomics Data Imputation

Spatially resolved transcriptomics represents a significant advancement in single-cell analysis by offering both gene expression data and their corresponding physical locations. However, this high degree of spatial resolution entails a drawback, as the resulting spatial transcriptomic data at the cellular level is notably plagued by a high incidence of missing values. Furthermore, most existing imputation methods either overlook the spatial information between spots or compromise the overall gene expression data distribution. To address these challenges, our primary focus is on effectively utilizing the spatial location information within spatial transcriptomic data to impute missing values, while preserving the overall data distribution. We introduce \textbf{stMCDI}, a novel conditional diffusion model for spatial transcriptomics data imputation, which employs a denoising network trained using randomly masked data portions as guidance, with the unmasked data serving as conditions. Additionally, it utilizes a GNN encoder to integrate the spatial position information, thereby enhancing model performance. The results obtained from spatial transcriptomics datasets elucidate the performance of our methods relative to existing approaches.

ICHPro: Intracerebral Hemorrhage Prognosis Classification Via Joint-attention Fusion-based 3d Cross-modal Network

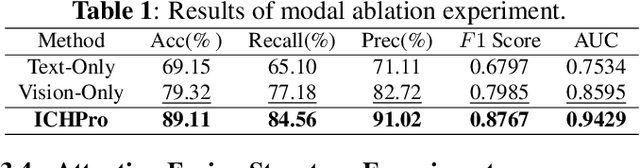
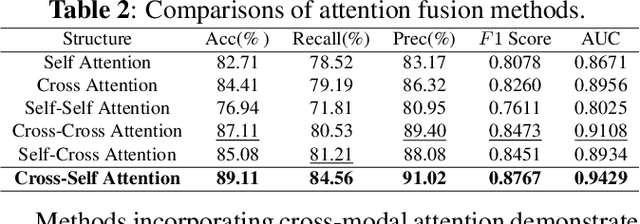
Intracerebral Hemorrhage (ICH) is the deadliest subtype of stroke, necessitating timely and accurate prognostic evaluation to reduce mortality and disability. However, the multi-factorial nature and complexity of ICH make methods based solely on computed tomography (CT) image features inadequate. Despite the capacity of cross-modal networks to fuse additional information, the effective combination of different modal features remains a significant challenge. In this study, we propose a joint-attention fusion-based 3D cross-modal network termed ICHPro that simulates the ICH prognosis interpretation process utilized by neurosurgeons. ICHPro includes a joint-attention fusion module to fuse features from CT images with demographic and clinical textual data. To enhance the representation of cross-modal features, we introduce a joint loss function. ICHPro facilitates the extraction of richer cross-modal features, thereby improving classification performance. Upon testing our method using a five-fold cross-validation, we achieved an accuracy of 89.11%, an F1 score of 0.8767, and an AUC value of 0.9429. These results outperform those obtained from other advanced methods based on the test dataset, thereby demonstrating the superior efficacy of ICHPro. The code is available at our Github: https://github.com/YU-deep/ICH.

Weighted Sparse Partial Least Squares for Joint Sample and Feature Selection

Sparse Partial Least Squares (sPLS) is a common dimensionality reduction technique for data fusion, which projects data samples from two views by seeking linear combinations with a small number of variables with the maximum variance. However, sPLS extracts the combinations between two data sets with all data samples so that it cannot detect latent subsets of samples. To extend the application of sPLS by identifying a specific subset of samples and remove outliers, we propose an $\ell_\infty/\ell_0$-norm constrained weighted sparse PLS ($\ell_\infty/\ell_0$-wsPLS) method for joint sample and feature selection, where the $\ell_\infty/\ell_0$-norm constrains are used to select a subset of samples. We prove that the $\ell_\infty/\ell_0$-norm constrains have the Kurdyka-\L{ojasiewicz}~property so that a globally convergent algorithm is developed to solve it. Moreover, multi-view data with a same set of samples can be available in various real problems. To this end, we extend the $\ell_\infty/\ell_0$-wsPLS model and propose two multi-view wsPLS models for multi-view data fusion. We develop an efficient iterative algorithm for each multi-view wsPLS model and show its convergence property. As well as numerical and biomedical data experiments demonstrate the efficiency of the proposed methods.

Structured Sparse Non-negative Matrix Factorization with L20-Norm for scRNA-seq Data Analysis

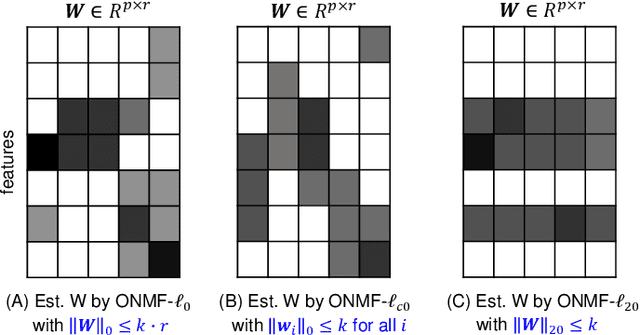
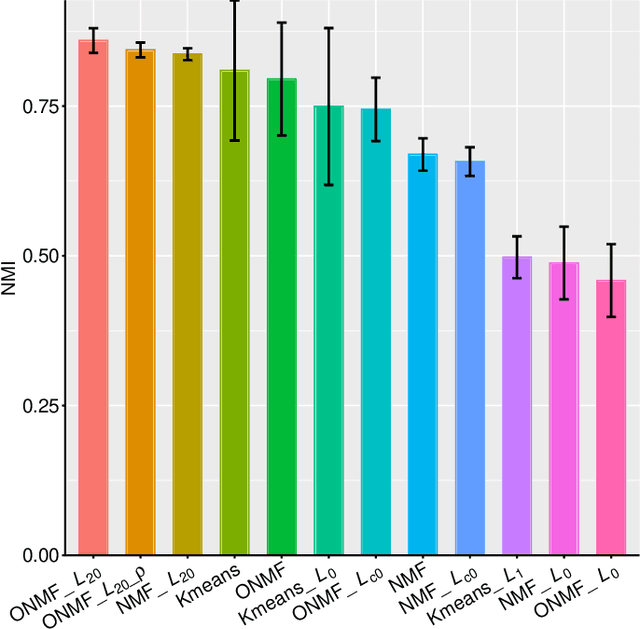
Non-negative matrix factorization (NMF) is a powerful tool for dimensionality reduction and clustering. Unfortunately, the interpretation of the clustering results from NMF is difficult, especially for the high-dimensional biological data without effective feature selection. In this paper, we first introduce a row-sparse NMF with $\ell_{2,0}$-norm constraint (NMF_$\ell_{20}$), where the basis matrix $W$ is constrained by the $\ell_{2,0}$-norm, such that $W$ has a row-sparsity pattern with feature selection. It is a challenge to solve the model, because the $\ell_{2,0}$-norm is non-convex and non-smooth. Fortunately, we prove that the $\ell_{2,0}$-norm satisfies the Kurdyka-\L{ojasiewicz} property. Based on the finding, we present a proximal alternating linearized minimization algorithm and its monotone accelerated version to solve the NMF_$\ell_{20}$ model. In addition, we also present a orthogonal NMF with $\ell_{2,0}$-norm constraint (ONMF_$\ell_{20}$) to enhance the clustering performance by using a non-negative orthogonal constraint. We propose an efficient algorithm to solve ONMF_$\ell_{20}$ by transforming it into a series of constrained and penalized matrix factorization problems. The results on numerical and scRNA-seq datasets demonstrate the efficiency of our methods in comparison with existing methods.