Weighted Sparse Partial Least Squares for Joint Sample and Feature Selection

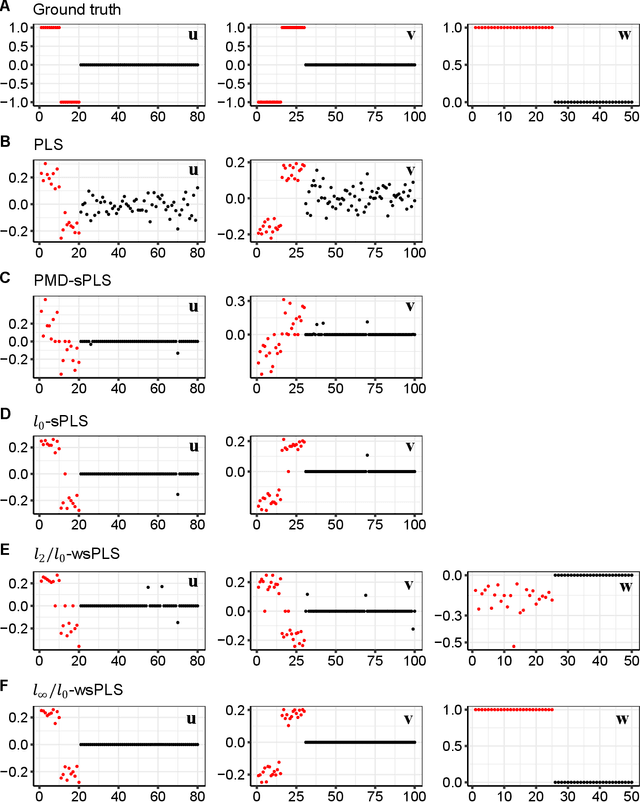
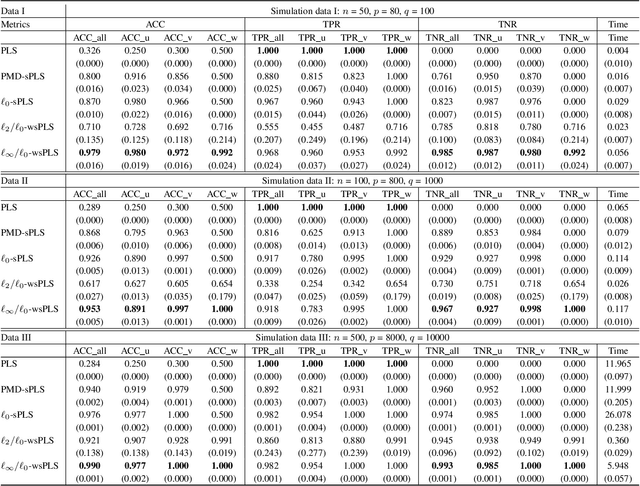
Sparse Partial Least Squares (sPLS) is a common dimensionality reduction technique for data fusion, which projects data samples from two views by seeking linear combinations with a small number of variables with the maximum variance. However, sPLS extracts the combinations between two data sets with all data samples so that it cannot detect latent subsets of samples. To extend the application of sPLS by identifying a specific subset of samples and remove outliers, we propose an $\ell_\infty/\ell_0$-norm constrained weighted sparse PLS ($\ell_\infty/\ell_0$-wsPLS) method for joint sample and feature selection, where the $\ell_\infty/\ell_0$-norm constrains are used to select a subset of samples. We prove that the $\ell_\infty/\ell_0$-norm constrains have the Kurdyka-\L{ojasiewicz}~property so that a globally convergent algorithm is developed to solve it. Moreover, multi-view data with a same set of samples can be available in various real problems. To this end, we extend the $\ell_\infty/\ell_0$-wsPLS model and propose two multi-view wsPLS models for multi-view data fusion. We develop an efficient iterative algorithm for each multi-view wsPLS model and show its convergence property. As well as numerical and biomedical data experiments demonstrate the efficiency of the proposed methods.