Structured Sparse Non-negative Matrix Factorization with L20-Norm for scRNA-seq Data Analysis
Paper and Code
Apr 27, 2021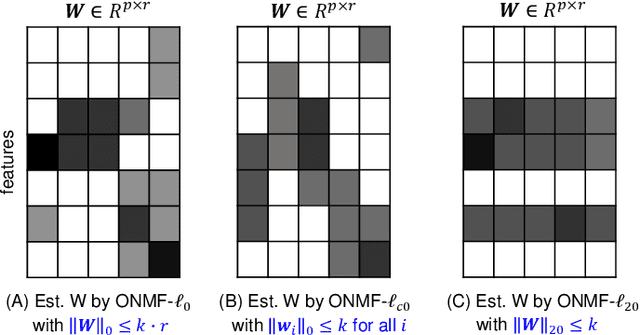

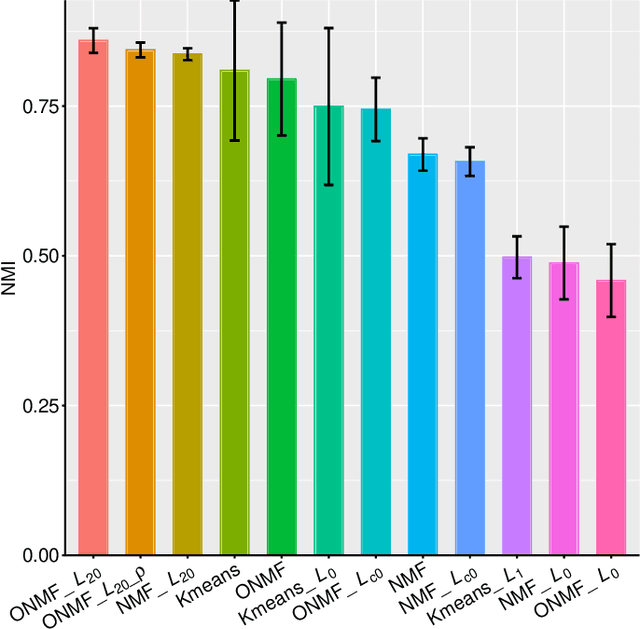

Non-negative matrix factorization (NMF) is a powerful tool for dimensionality reduction and clustering. Unfortunately, the interpretation of the clustering results from NMF is difficult, especially for the high-dimensional biological data without effective feature selection. In this paper, we first introduce a row-sparse NMF with $\ell_{2,0}$-norm constraint (NMF_$\ell_{20}$), where the basis matrix $W$ is constrained by the $\ell_{2,0}$-norm, such that $W$ has a row-sparsity pattern with feature selection. It is a challenge to solve the model, because the $\ell_{2,0}$-norm is non-convex and non-smooth. Fortunately, we prove that the $\ell_{2,0}$-norm satisfies the Kurdyka-\L{ojasiewicz} property. Based on the finding, we present a proximal alternating linearized minimization algorithm and its monotone accelerated version to solve the NMF_$\ell_{20}$ model. In addition, we also present a orthogonal NMF with $\ell_{2,0}$-norm constraint (ONMF_$\ell_{20}$) to enhance the clustering performance by using a non-negative orthogonal constraint. We propose an efficient algorithm to solve ONMF_$\ell_{20}$ by transforming it into a series of constrained and penalized matrix factorization problems. The results on numerical and scRNA-seq datasets demonstrate the efficiency of our methods in comparison with existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge