Random Forests for dependent data

Random forest (RF) is one of the most popular methods for estimating regression functions. The local nature of the RF algorithm, based on intra-node means and variances, is ideal when errors are i.i.d. For dependent error processes like time series and spatial settings where data in all the nodes will be correlated, operating locally ignores this dependence. Also, RF will involve resampling of correlated data, violating the principles of bootstrap. Theoretically, consistency of RF has been established for i.i.d. errors, but little is known about the case of dependent errors. We propose RF-GLS, a novel extension of RF for dependent error processes in the same way Generalized Least Squares (GLS) fundamentally extends Ordinary Least Squares (OLS) for linear models under dependence. The key to this extension is the equivalent representation of the local decision-making in a regression tree as a global OLS optimization which is then replaced with a GLS loss to create a GLS-style regression tree. This also synergistically addresses the resampling issue, as the use of GLS loss amounts to resampling uncorrelated contrasts (pre-whitened data) instead of the correlated data. For spatial settings, RF-GLS can be used in conjunction with Gaussian Process correlated errors to generate kriging predictions at new locations. RF becomes a special case of RF-GLS with an identity working covariance matrix. We establish consistency of RF-GLS under beta- (absolutely regular) mixing error processes and show that this general result subsumes important cases like autoregressive time series and spatial Matern Gaussian Processes. As a byproduct, we also establish consistency of RF for beta-mixing processes, which to our knowledge, is the first such result for RF under dependence. We empirically demonstrate the improvement achieved by RF-GLS over RF for both estimation and prediction under dependence.

A Debiased MDI Feature Importance Measure for Random Forests

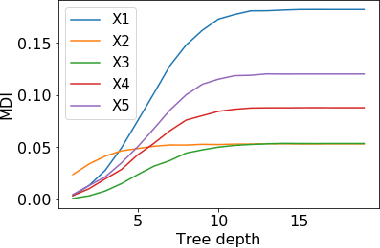
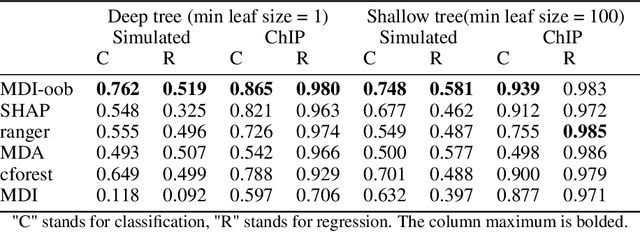
Tree ensembles such as Random Forests have achieved impressive empirical success across a wide variety of applications. To understand how these models make predictions, people routinely turn to feature importance measures calculated from tree ensembles. It has long been known that Mean Decrease Impurity (MDI), one of the most widely used measures of feature importance, incorrectly assigns high importance to noisy features, leading to systematic bias in feature selection. In this paper, we address the feature selection bias of MDI from both theoretical and methodological perspectives. Based on the original definition of MDI by Breiman et al. for a single tree, we derive a tight non-asymptotic bound on the expected bias of MDI importance of noisy features, showing that deep trees have higher (expected) feature selection bias than shallow ones. However, it is not clear how to reduce the bias of MDI using its existing analytical expression. We derive a new analytical expression for MDI, and based on this new expression, we are able to propose a debiased MDI feature importance measure using out-of-bag samples, called MDI-oob. For both the simulated data and a genomic ChIP dataset, MDI-oob achieves state-of-the-art performance in feature selection from Random Forests for both deep and shallow trees.

Large Spectral Density Matrix Estimation by Thresholding

Spectral density matrix estimation of multivariate time series is a classical problem in time series and signal processing. In modern neuroscience, spectral density based metrics are commonly used for analyzing functional connectivity among brain regions. In this paper, we develop a non-asymptotic theory for regularized estimation of high-dimensional spectral density matrices of Gaussian and linear processes using thresholded versions of averaged periodograms. Our theoretical analysis ensures that consistent estimation of spectral density matrix of a $p$-dimensional time series using $n$ samples is possible under high-dimensional regime $\log p / n \rightarrow 0$ as long as the true spectral density is approximately sparse. A key technical component of our analysis is a new concentration inequality of average periodogram around its expectation, which is of independent interest. Our estimation consistency results complement existing results for shrinkage based estimators of multivariate spectral density, which require no assumption on sparsity but only ensure consistent estimation in a regime $p^2/n \rightarrow 0$. In addition, our proposed thresholding based estimators perform consistent and automatic edge selection when learning coherence networks among the components of a multivariate time series. We demonstrate the advantage of our estimators using simulation studies and a real data application on functional connectivity analysis with fMRI data.

Refining interaction search through signed iterative Random Forests

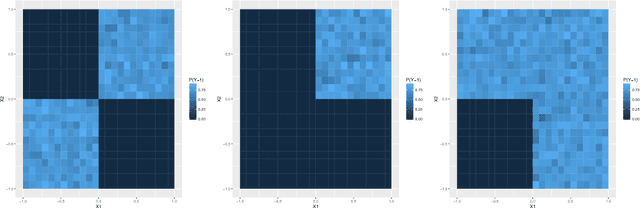
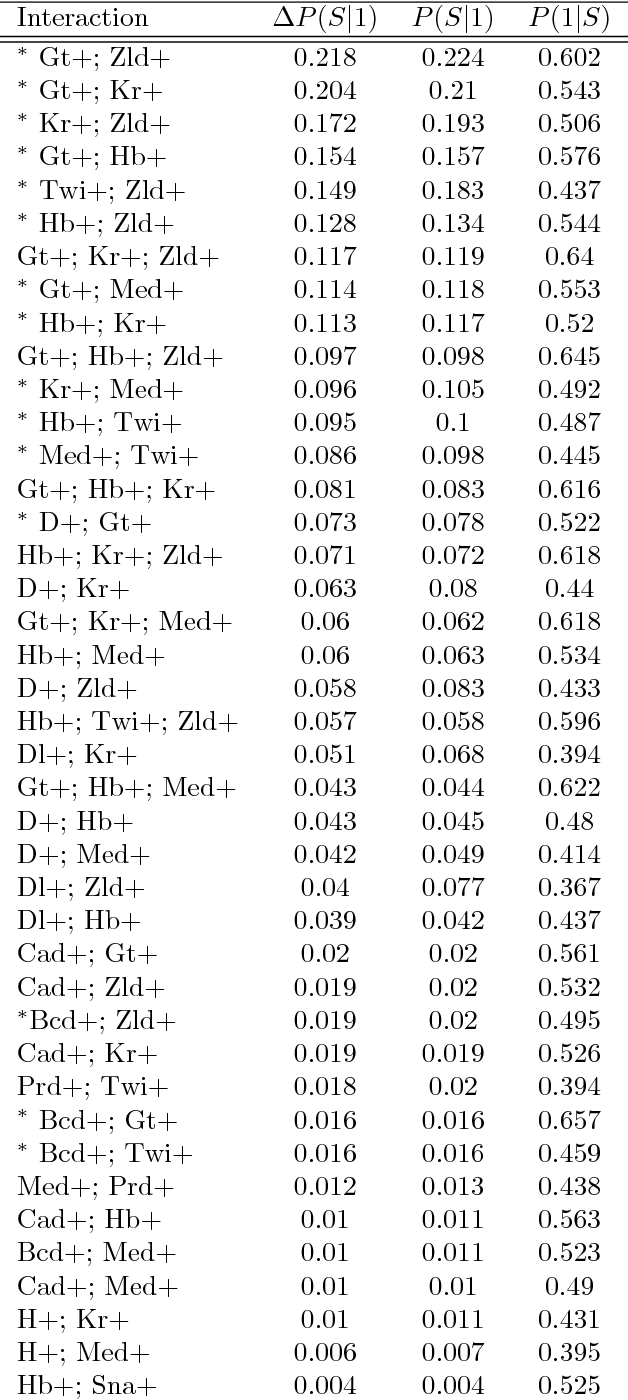
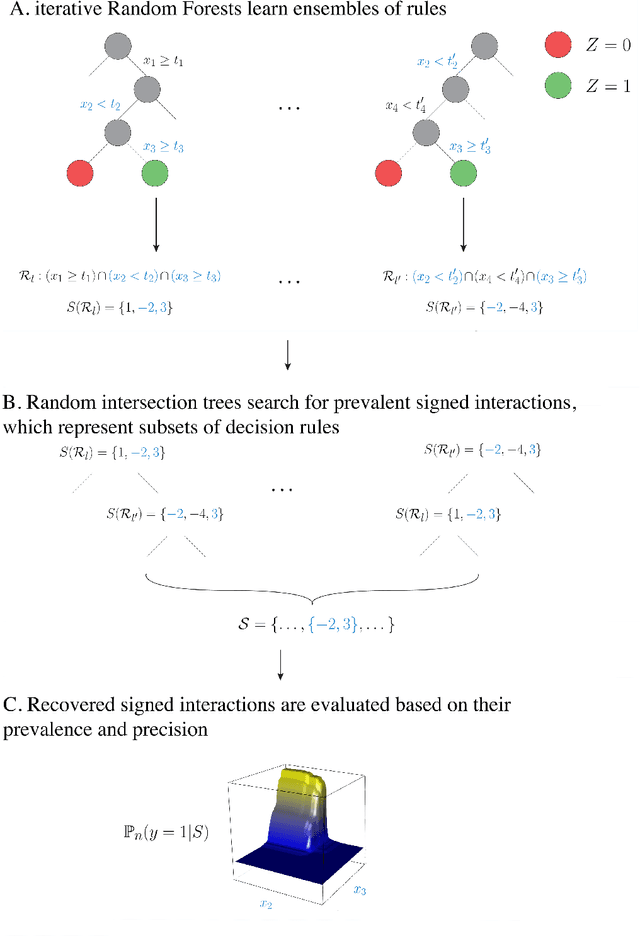
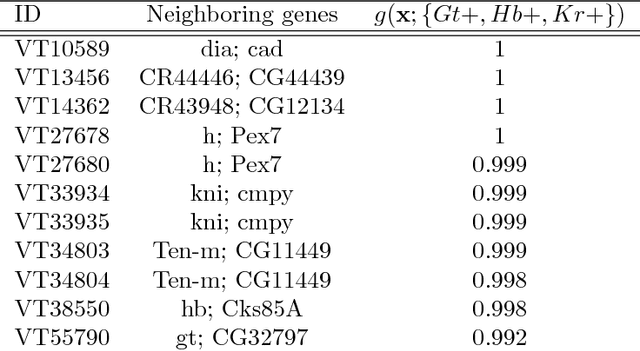
Advances in supervised learning have enabled accurate prediction in biological systems governed by complex interactions among biomolecules. However, state-of-the-art predictive algorithms are typically black-boxes, learning statistical interactions that are difficult to translate into testable hypotheses. The iterative Random Forest algorithm took a step towards bridging this gap by providing a computationally tractable procedure to identify the stable, high-order feature interactions that drive the predictive accuracy of Random Forests (RF). Here we refine the interactions identified by iRF to explicitly map responses as a function of interacting features. Our method, signed iRF, describes subsets of rules that frequently occur on RF decision paths. We refer to these rule subsets as signed interactions. Signed interactions share not only the same set of interacting features but also exhibit similar thresholding behavior, and thus describe a consistent functional relationship between interacting features and responses. We describe stable and predictive importance metrics to rank signed interactions. For each SPIM, we define null importance metrics that characterize its expected behavior under known structure. We evaluate our proposed approach in biologically inspired simulations and two case studies: predicting enhancer activity and spatial gene expression patterns. In the case of enhancer activity, s-iRF recovers one of the few experimentally validated high-order interactions and suggests novel enhancer elements where this interaction may be active. In the case of spatial gene expression patterns, s-iRF recovers all 11 reported links in the gap gene network. By refining the process of interaction recovery, our approach has the potential to guide mechanistic inquiry into systems whose scale and complexity is beyond human comprehension.

High Dimensional Estimation and Multi-Factor Models

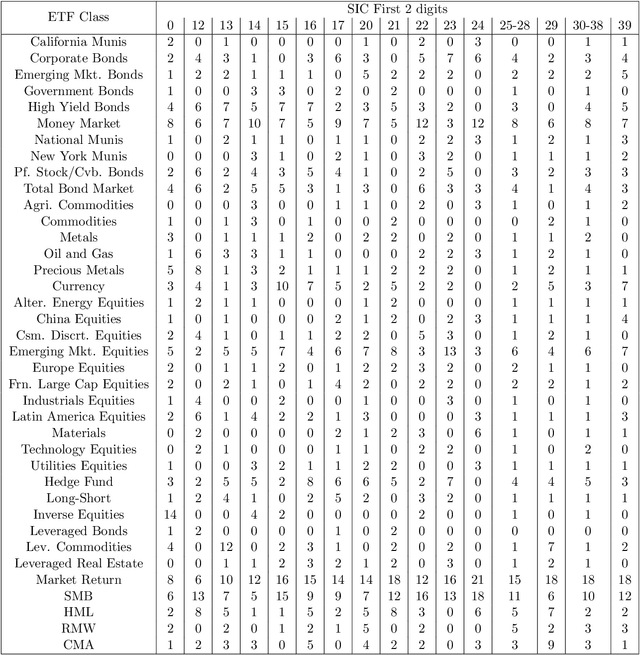
This paper re-investigates the estimation of multiple factor models relaxing the convention that the number of factors is small and using a new approach for identifying factors. We first obtain the collection of all possible factors and then provide a simultaneous test, security by security, of which factors are significant. Since the collection of risk factors is large and highly correlated, high-dimension methods (including the LASSO and prototype clustering) have to be used. The multi-factor model is shown to have a significantly better fit than the Fama-French 5-factor model. Robustness tests are also provided.

Iterative Random Forests to detect predictive and stable high-order interactions

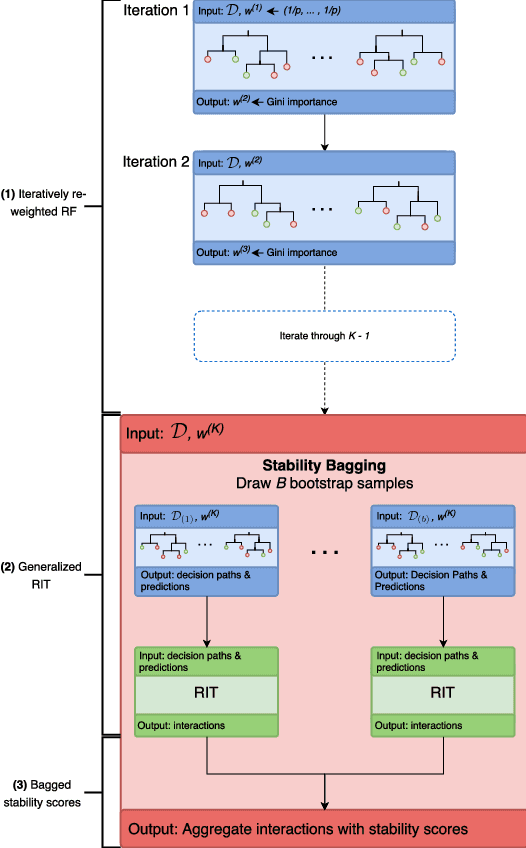
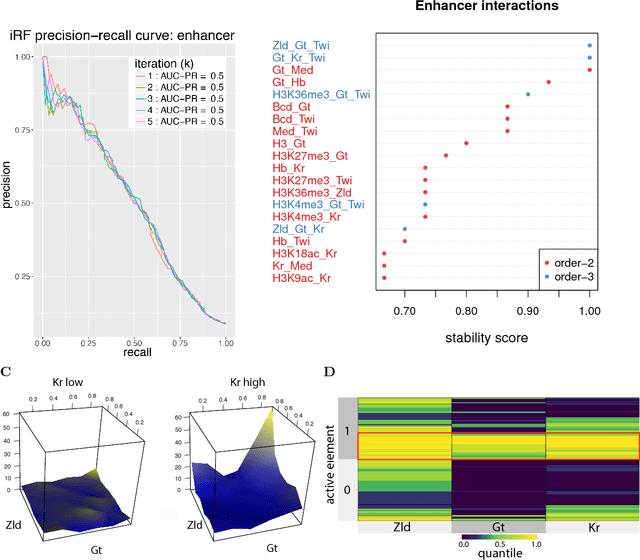
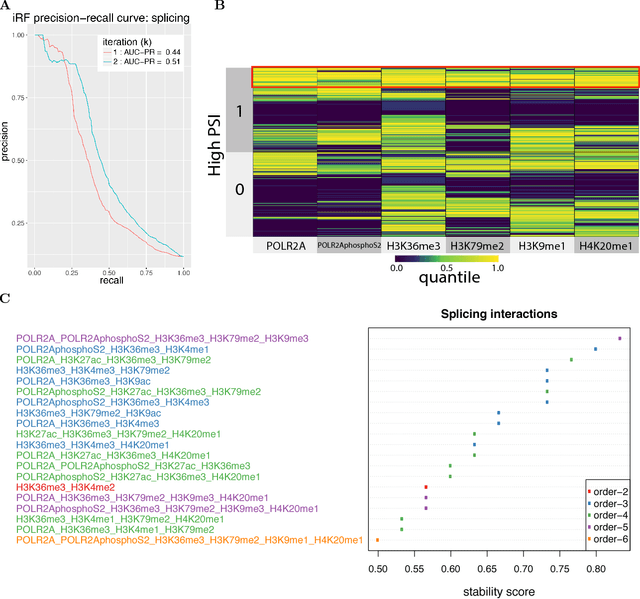
Genomics has revolutionized biology, enabling the interrogation of whole transcriptomes, genome-wide binding sites for proteins, and many other molecular processes. However, individual genomic assays measure elements that interact in vivo as components of larger molecular machines. Understanding how these high-order interactions drive gene expression presents a substantial statistical challenge. Building on Random Forests (RF), Random Intersection Trees (RITs), and through extensive, biologically inspired simulations, we developed the iterative Random Forest algorithm (iRF). iRF trains a feature-weighted ensemble of decision trees to detect stable, high-order interactions with same order of computational cost as RF. We demonstrate the utility of iRF for high-order interaction discovery in two prediction problems: enhancer activity in the early Drosophila embryo and alternative splicing of primary transcripts in human derived cell lines. In Drosophila, among the 20 pairwise transcription factor interactions iRF identifies as stable (returned in more than half of bootstrap replicates), 80% have been previously reported as physical interactions. Moreover, novel third-order interactions, e.g. between Zelda (Zld), Giant (Gt), and Twist (Twi), suggest high-order relationships that are candidates for follow-up experiments. In human-derived cells, iRF re-discovered a central role of H3K36me3 in chromatin-mediated splicing regulation, and identified novel 5th and 6th order interactions, indicative of multi-valent nucleosomes with specific roles in splicing regulation. By decoupling the order of interactions from the computational cost of identification, iRF opens new avenues of inquiry into the molecular mechanisms underlying genome biology.

Interpretable Vector AutoRegressions with Exogenous Time Series

The Vector AutoRegressive (VAR) model is fundamental to the study of multivariate time series. Although VAR models are intensively investigated by many researchers, practitioners often show more interest in analyzing VARX models that incorporate the impact of unmodeled exogenous variables (X) into the VAR. However, since the parameter space grows quadratically with the number of time series, estimation quickly becomes challenging. While several proposals have been made to sparsely estimate large VAR models, the estimation of large VARX models is under-explored. Moreover, typically these sparse proposals involve a lasso-type penalty and do not incorporate lag selection into the estimation procedure. As a consequence, the resulting models may be difficult to interpret. In this paper, we propose a lag-based hierarchically sparse estimator, called "HVARX", for large VARX models. We illustrate the usefulness of HVARX on a cross-category management marketing application. Our results show how it provides a highly interpretable model, and improves out-of-sample forecast accuracy compared to a lasso-type approach.