Heterogeneous Transfer Learning for Building High-Dimensional Generalized Linear Models with Disparate Datasets

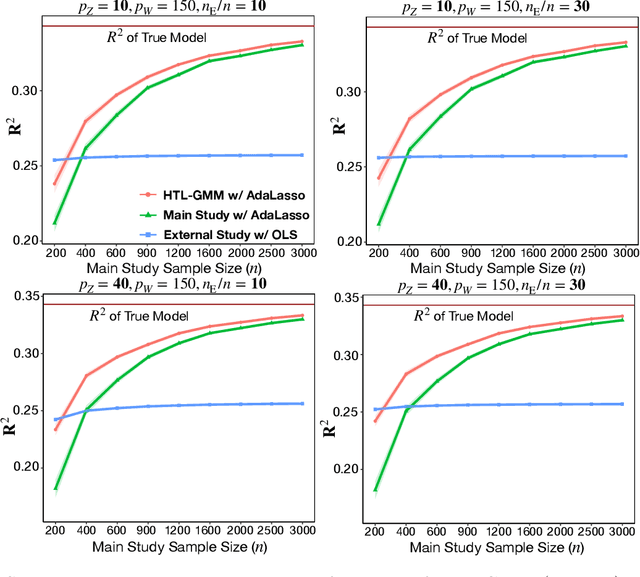
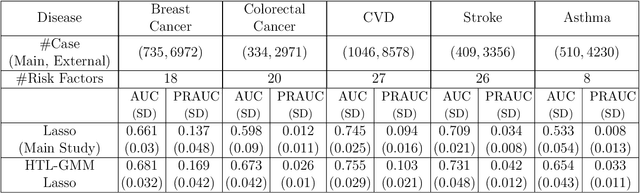
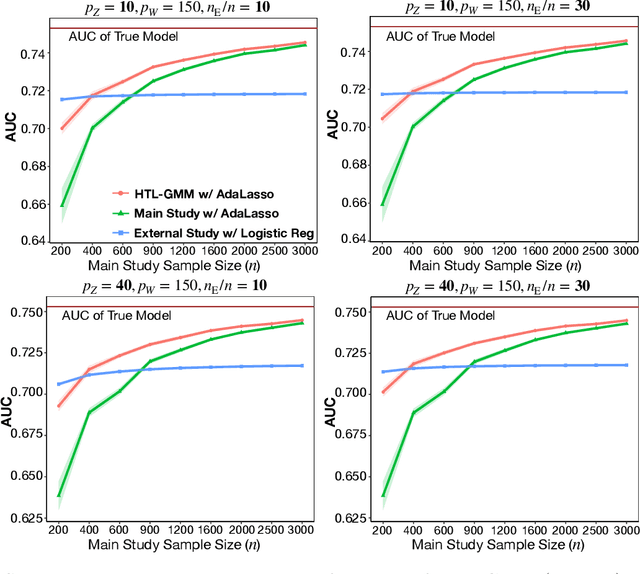
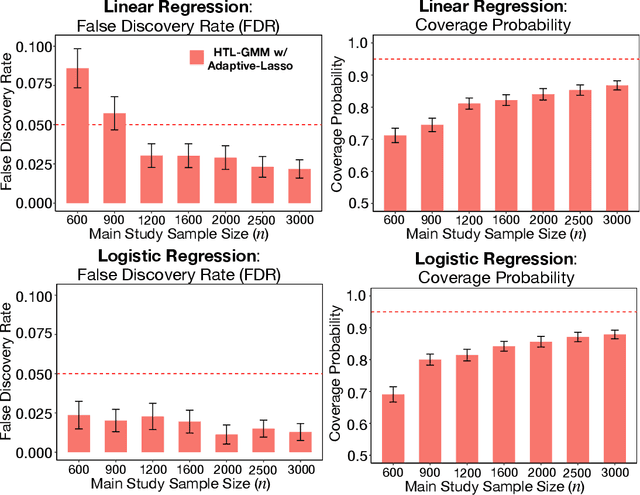
Development of comprehensive prediction models are often of great interest in many disciplines of science, but datasets with information on all desired features typically have small sample sizes. In this article, we describe a transfer learning approach for building high-dimensional generalized linear models using data from a main study that has detailed information on all predictors, and from one or more external studies that have ascertained a more limited set of predictors. We propose using the external dataset(s) to build reduced model(s) and then transfer the information on underlying parameters for the analysis of the main study through a set of calibration equations, while accounting for the study-specific effects of certain design variables. We then use a generalized method of moment (GMM) with penalization for parameter estimation and develop highly scalable algorithms for fitting models taking advantage of the popular glmnet package. We further show that the use of adaptive-Lasso penalty leads to the oracle property of underlying parameter estimates and thus leads to convenient post-selection inference procedures. We conduct extensive simulation studies to investigate both predictive performance and post-selection inference properties of the proposed method. Finally, we illustrate a timely application of the proposed method for the development of risk prediction models for five common diseases using the UK Biobank study, combining baseline information from all study participants (500K) and recently released high-throughout proteomic data (# protein = 1500) on a subset (50K) of the participants.

Random forests for binary geospatial data

Binary geospatial data is commonly analyzed with generalized linear mixed models, specified with a linear fixed covariate effect and a Gaussian Process (GP)-distributed spatial random effect, relating to the response via a link function. The assumption of linear covariate effects is severely restrictive. Random Forests (RF) are increasingly being used for non-linear modeling of spatial data, but current extensions of RF for binary spatial data depart the mixed model setup, relinquishing inference on the fixed effects and other advantages of using GP. We propose RF-GP, using Random Forests for estimating the non-linear covariate effect and Gaussian Processes for modeling the spatial random effects directly within the generalized mixed model framework. We observe and exploit equivalence of Gini impurity measure and least squares loss to propose an extension of RF for binary data that accounts for the spatial dependence. We then propose a novel link inversion algorithm that leverages the properties of GP to estimate the covariate effects and offer spatial predictions. RF-GP outperforms existing RF methods for estimation and prediction in both simulated and real-world data. We establish consistency of RF-GP for a general class of $\beta$-mixing binary processes that includes common choices like spatial Mat\'ern GP and autoregressive processes.

Inferring independent sets of Gaussian variables after thresholding correlations

We consider testing whether a set of Gaussian variables, selected from the data, is independent of the remaining variables. We assume that this set is selected via a very simple approach that is commonly used across scientific disciplines: we select a set of variables for which the correlation with all variables outside the set falls below some threshold. Unlike other settings in selective inference, failure to account for the selection step leads, in this setting, to excessively conservative (as opposed to anti-conservative) results. Our proposed test properly accounts for the fact that the set of variables is selected from the data, and thus is not overly conservative. To develop our test, we condition on the event that the selection resulted in the set of variables in question. To achieve computational tractability, we develop a new characterization of the conditioning event in terms of the canonical correlation between the groups of random variables. In simulation studies and in the analysis of gene co-expression networks, we show that our approach has much higher power than a ``naive'' approach that ignores the effect of selection.

Random Forests for dependent data

Random forest (RF) is one of the most popular methods for estimating regression functions. The local nature of the RF algorithm, based on intra-node means and variances, is ideal when errors are i.i.d. For dependent error processes like time series and spatial settings where data in all the nodes will be correlated, operating locally ignores this dependence. Also, RF will involve resampling of correlated data, violating the principles of bootstrap. Theoretically, consistency of RF has been established for i.i.d. errors, but little is known about the case of dependent errors. We propose RF-GLS, a novel extension of RF for dependent error processes in the same way Generalized Least Squares (GLS) fundamentally extends Ordinary Least Squares (OLS) for linear models under dependence. The key to this extension is the equivalent representation of the local decision-making in a regression tree as a global OLS optimization which is then replaced with a GLS loss to create a GLS-style regression tree. This also synergistically addresses the resampling issue, as the use of GLS loss amounts to resampling uncorrelated contrasts (pre-whitened data) instead of the correlated data. For spatial settings, RF-GLS can be used in conjunction with Gaussian Process correlated errors to generate kriging predictions at new locations. RF becomes a special case of RF-GLS with an identity working covariance matrix. We establish consistency of RF-GLS under beta- (absolutely regular) mixing error processes and show that this general result subsumes important cases like autoregressive time series and spatial Matern Gaussian Processes. As a byproduct, we also establish consistency of RF for beta-mixing processes, which to our knowledge, is the first such result for RF under dependence. We empirically demonstrate the improvement achieved by RF-GLS over RF for both estimation and prediction under dependence.