Heterogeneous Transfer Learning for Building High-Dimensional Generalized Linear Models with Disparate Datasets
Paper and Code
Dec 20, 2023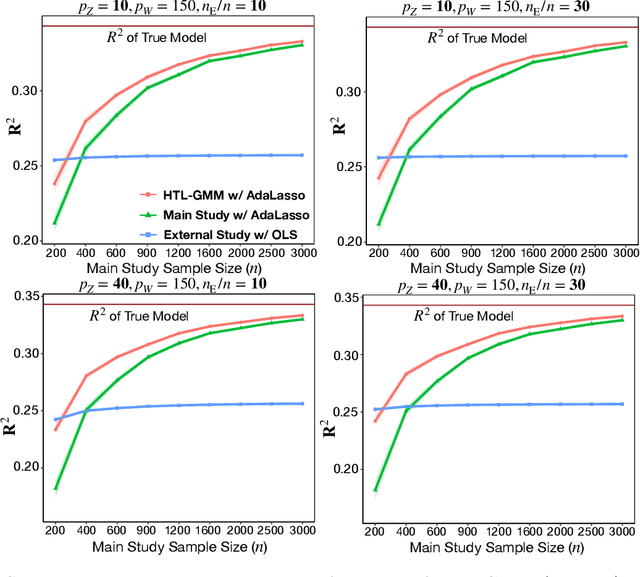
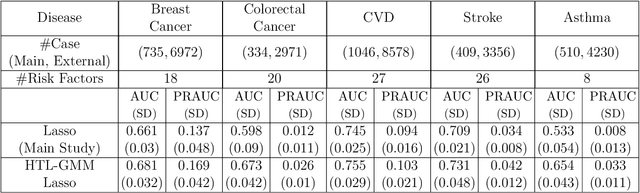
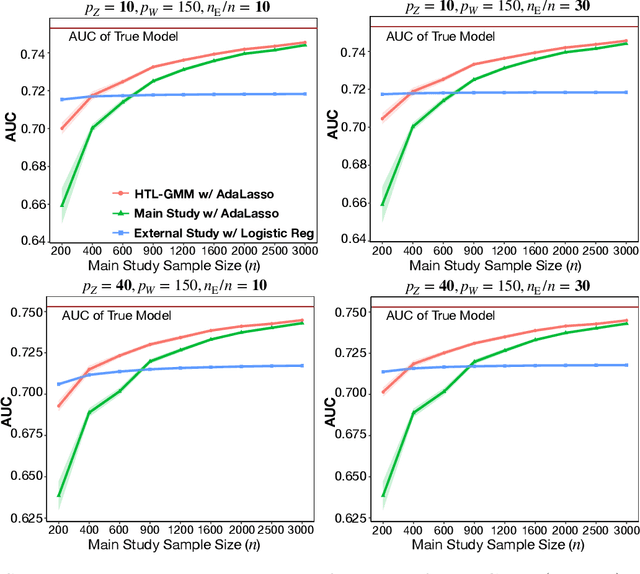
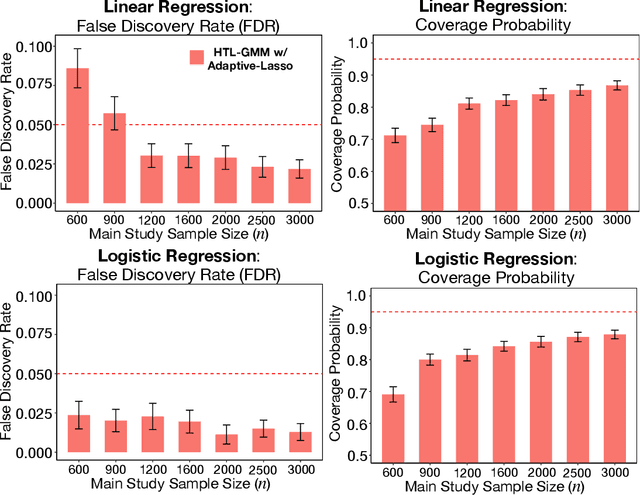
Development of comprehensive prediction models are often of great interest in many disciplines of science, but datasets with information on all desired features typically have small sample sizes. In this article, we describe a transfer learning approach for building high-dimensional generalized linear models using data from a main study that has detailed information on all predictors, and from one or more external studies that have ascertained a more limited set of predictors. We propose using the external dataset(s) to build reduced model(s) and then transfer the information on underlying parameters for the analysis of the main study through a set of calibration equations, while accounting for the study-specific effects of certain design variables. We then use a generalized method of moment (GMM) with penalization for parameter estimation and develop highly scalable algorithms for fitting models taking advantage of the popular glmnet package. We further show that the use of adaptive-Lasso penalty leads to the oracle property of underlying parameter estimates and thus leads to convenient post-selection inference procedures. We conduct extensive simulation studies to investigate both predictive performance and post-selection inference properties of the proposed method. Finally, we illustrate a timely application of the proposed method for the development of risk prediction models for five common diseases using the UK Biobank study, combining baseline information from all study participants (500K) and recently released high-throughout proteomic data (# protein = 1500) on a subset (50K) of the participants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge