MLExchange: A web-based platform enabling exchangeable machine learning workflows

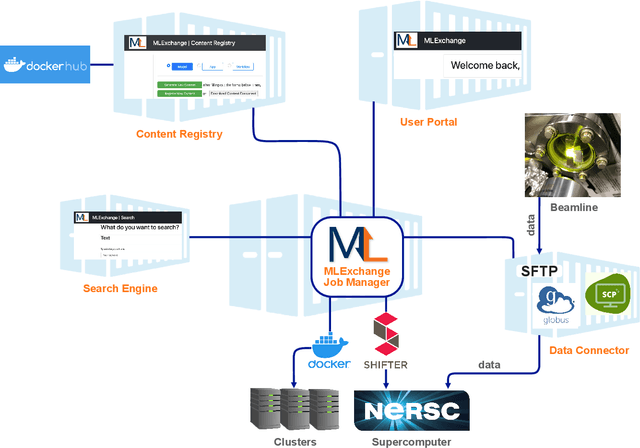
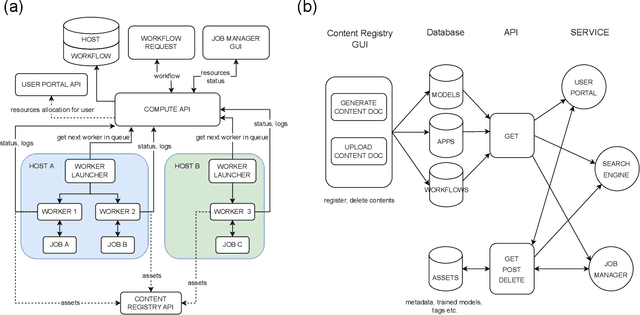
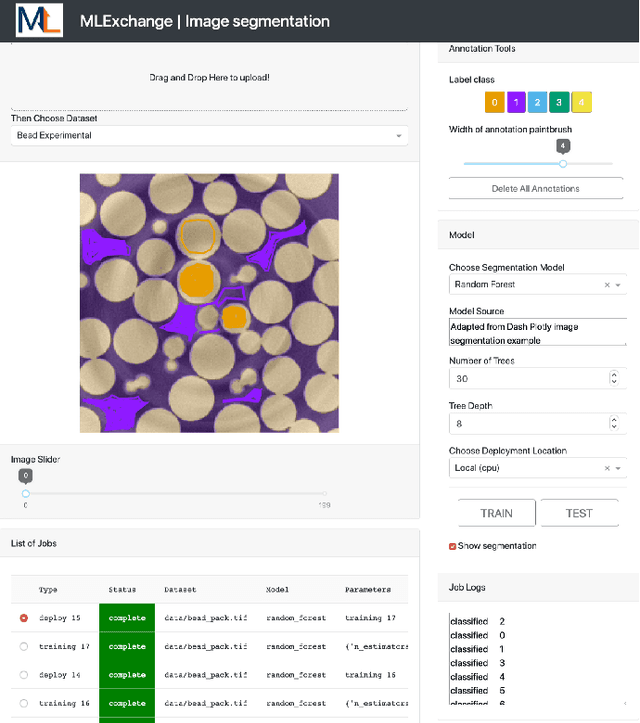
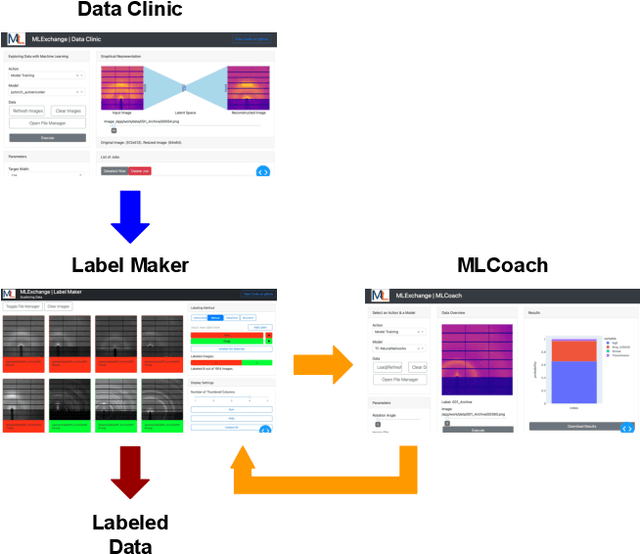
Machine learning (ML) algorithms are showing a growing trend in helping the scientific communities across different disciplines and institutions to address large and diverse data problems. However, many available ML tools are programmatically demanding and computationally costly. The MLExchange project aims to build a collaborative platform equipped with enabling tools that allow scientists and facility users who do not have a profound ML background to use ML and computational resources in scientific discovery. At the high level, we are targeting a full user experience where managing and exchanging ML algorithms, workflows, and data are readily available through web applications. So far, we have built four major components, i.e, the central job manager, the centralized content registry, user portal, and search engine, and successfully deployed these components on a testing server. Since each component is an independent container, the whole platform or its individual service(s) can be easily deployed at servers of different scales, ranging from a laptop (usually a single user) to high performance clusters (HPC) accessed (simultaneously) by many users. Thus, MLExchange renders flexible using scenarios -- users could either access the services and resources from a remote server or run the whole platform or its individual service(s) within their local network.

AutoPhaseNN: Unsupervised Physics-aware Deep Learning of 3D Nanoscale Coherent Imaging

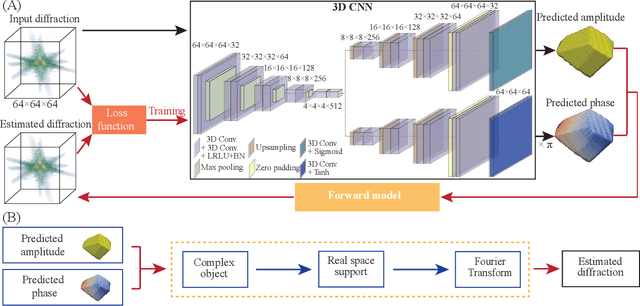
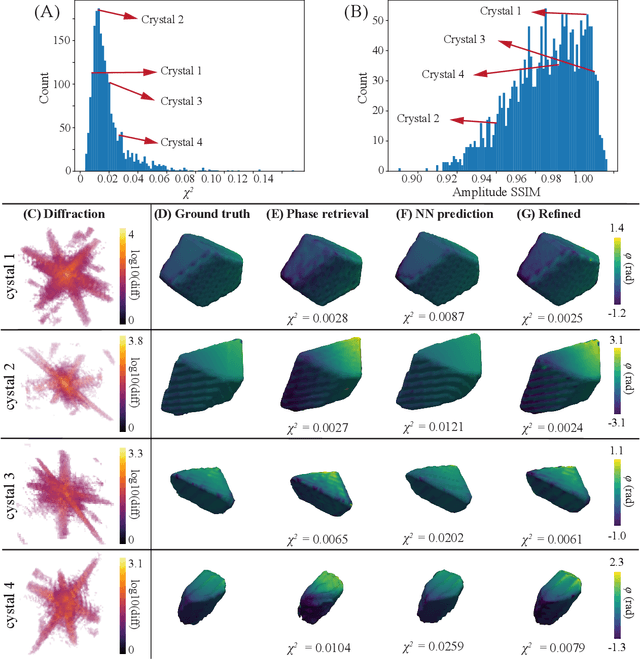
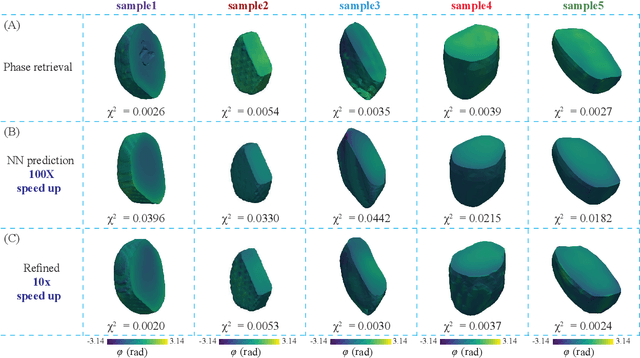
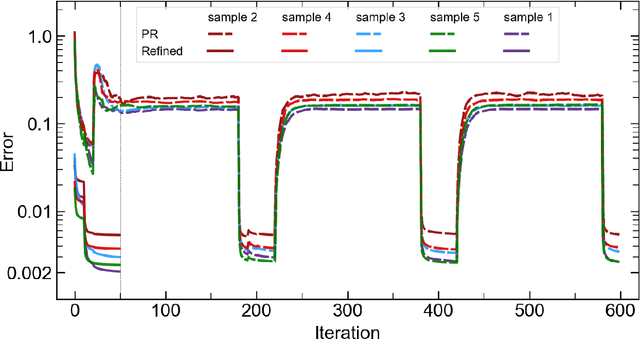
The problem of phase retrieval, or the algorithmic recovery of lost phase information from measured intensity alone, underlies various imaging methods from astronomy to nanoscale imaging. Traditional methods of phase retrieval are iterative in nature, and are therefore computationally expensive and time consuming. More recently, deep learning (DL) models have been developed to either provide learned priors to iterative phase retrieval or in some cases completely replace phase retrieval with networks that learn to recover the lost phase information from measured intensity alone. However, such models require vast amounts of labeled data, which can only be obtained through simulation or performing computationally prohibitive phase retrieval on hundreds of or even thousands of experimental datasets. Using a 3D nanoscale X-ray imaging modality (Bragg Coherent Diffraction Imaging or BCDI) as a representative technique, we demonstrate AutoPhaseNN, a DL-based approach which learns to solve the phase problem without labeled data. By incorporating the physics of the imaging technique into the DL model during training, AutoPhaseNN learns to invert 3D BCDI data from reciprocal space to real space in a single shot without ever being shown real space images. Once trained, AutoPhaseNN is about one hundred times faster than traditional iterative phase retrieval methods while providing comparable image quality.

Real-time 3D Nanoscale Coherent Imaging via Physics-aware Deep Learning

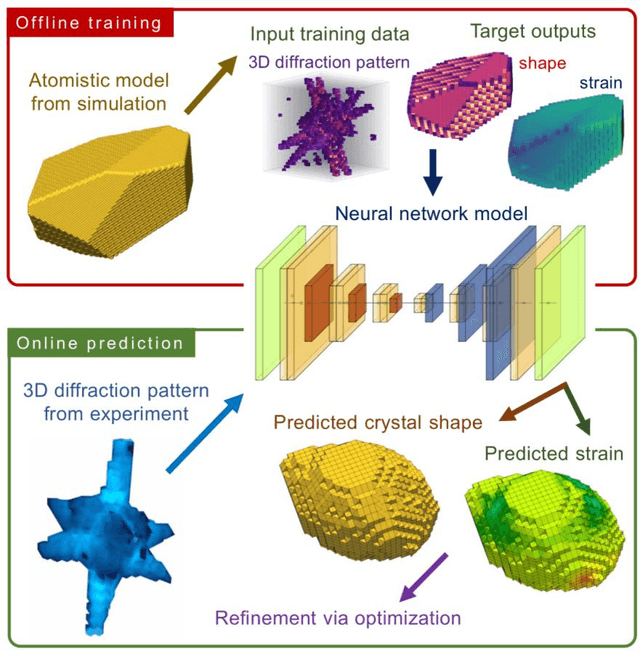
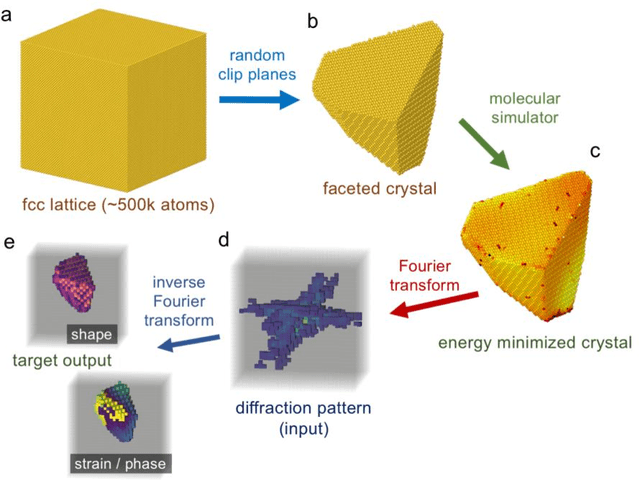
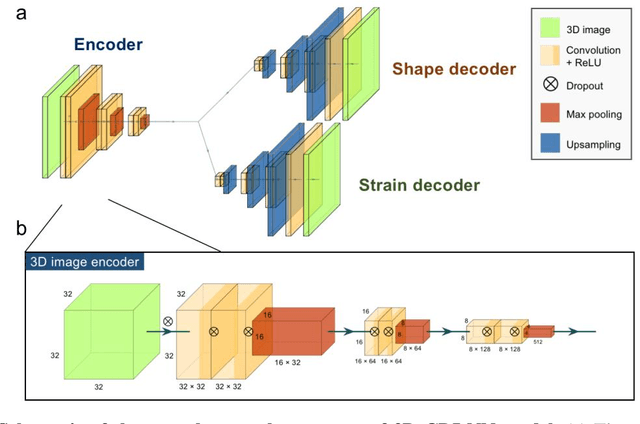
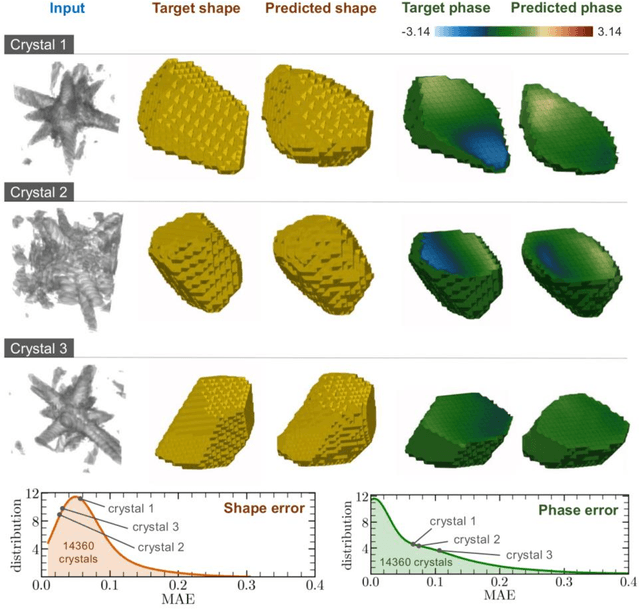
Phase retrieval, the problem of recovering lost phase information from measured intensity alone, is an inverse problem that is widely faced in various imaging modalities ranging from astronomy to nanoscale imaging. The current process of phase recovery is iterative in nature. As a result, the image formation is time-consuming and computationally expensive, precluding real-time imaging. Here, we use 3D nanoscale X-ray imaging as a representative example to develop a deep learning model to address this phase retrieval problem. We introduce 3D-CDI-NN, a deep convolutional neural network and differential programming framework trained to predict 3D structure and strain solely from input 3D X-ray coherent scattering data. Our networks are designed to be "physics-aware" in multiple aspects; in that the physics of x-ray scattering process is explicitly enforced in the training of the network, and the training data are drawn from atomistic simulations that are representative of the physics of the material. We further refine the neural network prediction through a physics-based optimization procedure to enable maximum accuracy at lowest computational cost. 3D-CDI-NN can invert a 3D coherent diffraction pattern to real-space structure and strain hundreds of times faster than traditional iterative phase retrieval methods, with negligible loss in accuracy. Our integrated machine learning and differential programming solution to the phase retrieval problem is broadly applicable across inverse problems in other application areas.

Combinatorial Black-Box Optimization with Expert Advice

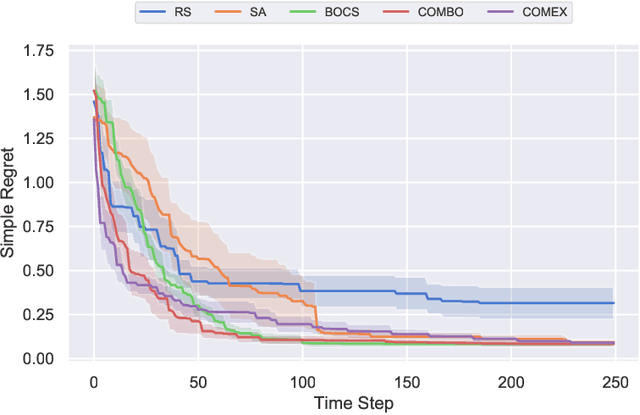
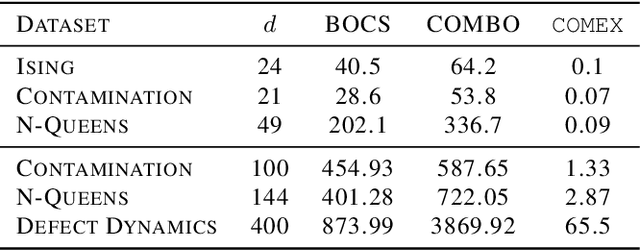
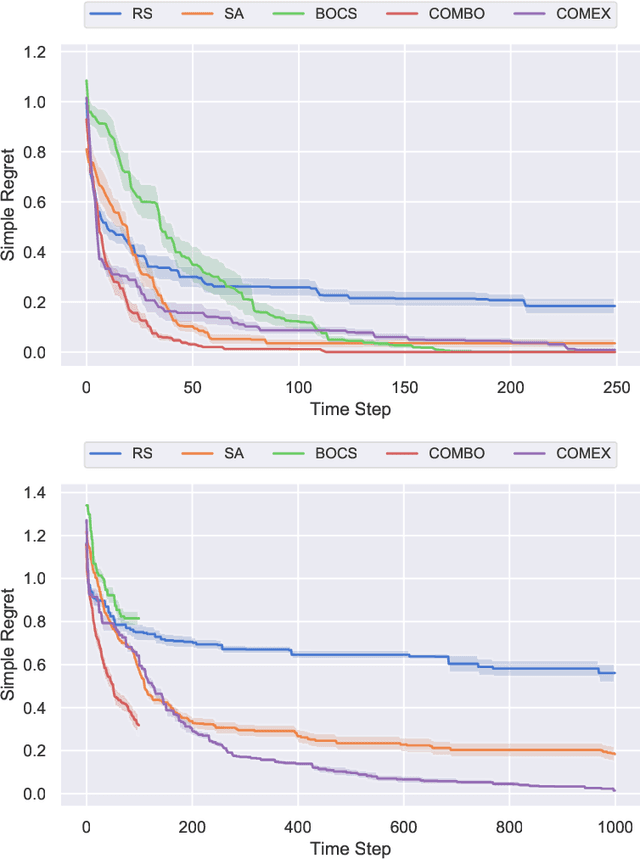
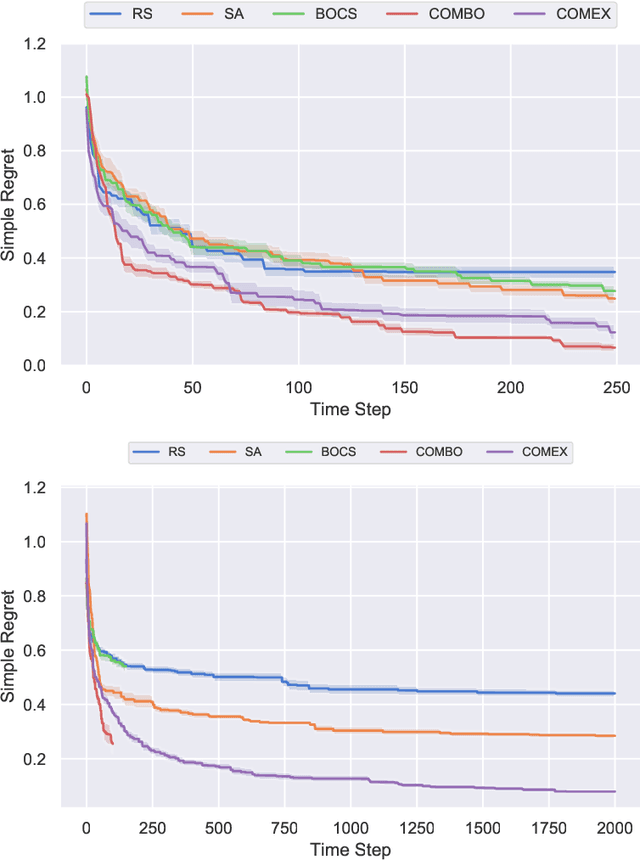
We consider the problem of black-box function optimization over the boolean hypercube. Despite the vast literature on black-box function optimization over continuous domains, not much attention has been paid to learning models for optimization over combinatorial domains until recently. However, the computational complexity of the recently devised algorithms are prohibitive even for moderate numbers of variables; drawing one sample using the existing algorithms is more expensive than a function evaluation for many black-box functions of interest. To address this problem, we propose a computationally efficient model learning algorithm based on multilinear polynomials and exponential weight updates. In the proposed algorithm, we alternate between simulated annealing with respect to the current polynomial representation and updating the weights using monomial experts' advice. Numerical experiments on various datasets in both unconstrained and sum-constrained boolean optimization indicate the competitive performance of the proposed algorithm, while improving the computational time up to several orders of magnitude compared to state-of-the-art algorithms in the literature.