Combinatorial Black-Box Optimization with Expert Advice
Paper and Code
Jun 06, 2020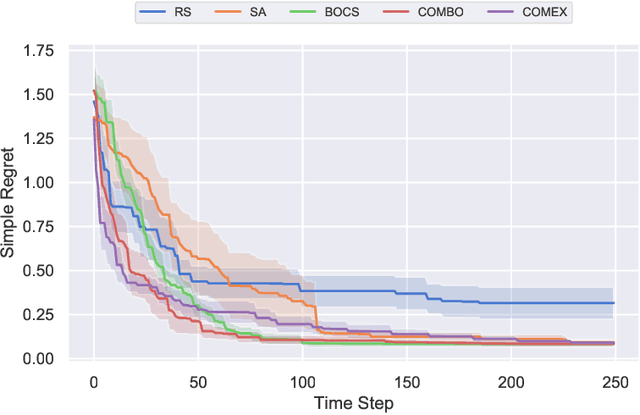
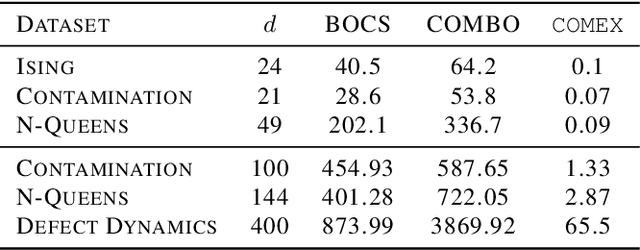
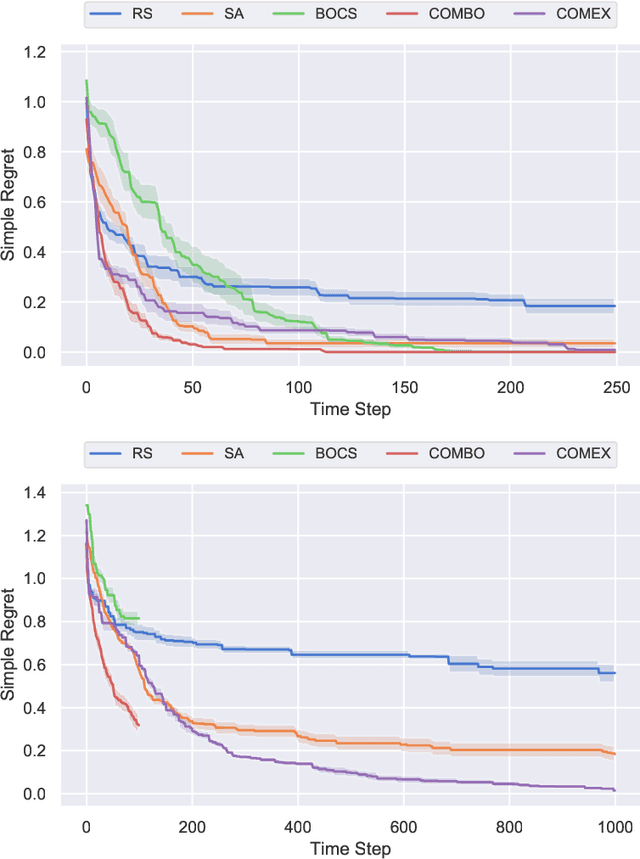
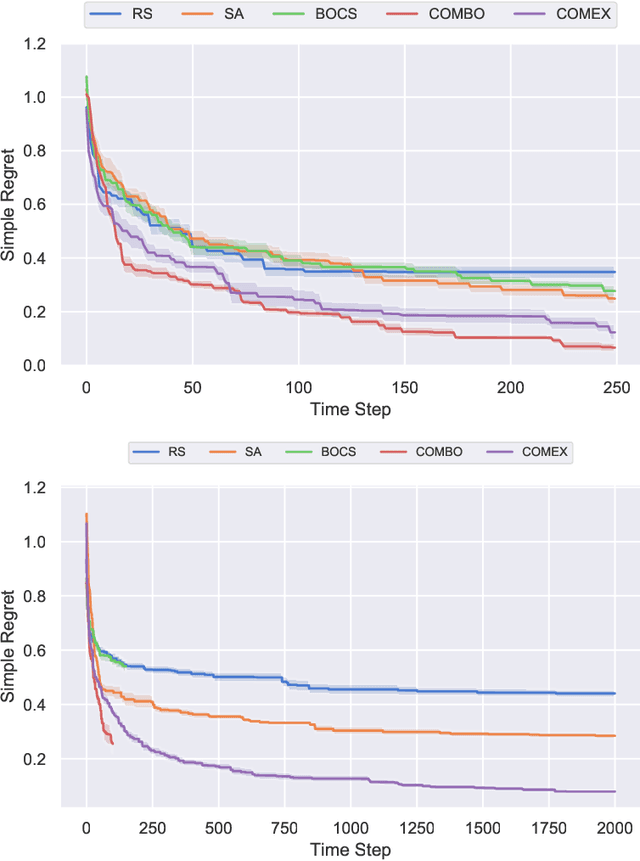
We consider the problem of black-box function optimization over the boolean hypercube. Despite the vast literature on black-box function optimization over continuous domains, not much attention has been paid to learning models for optimization over combinatorial domains until recently. However, the computational complexity of the recently devised algorithms are prohibitive even for moderate numbers of variables; drawing one sample using the existing algorithms is more expensive than a function evaluation for many black-box functions of interest. To address this problem, we propose a computationally efficient model learning algorithm based on multilinear polynomials and exponential weight updates. In the proposed algorithm, we alternate between simulated annealing with respect to the current polynomial representation and updating the weights using monomial experts' advice. Numerical experiments on various datasets in both unconstrained and sum-constrained boolean optimization indicate the competitive performance of the proposed algorithm, while improving the computational time up to several orders of magnitude compared to state-of-the-art algorithms in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge