Troy David Loeffler
Machine learning for interpreting coherent X-ray speckle patterns
Nov 15, 2022Abstract:Speckle patterns produced by coherent X-ray have a close relationship with the internal structure of materials but quantitative inversion of the relationship to determine structure from images is challenging. Here, we investigate the link between coherent X-ray speckle patterns and sample structures using a model 2D disk system and explore the ability of machine learning to learn aspects of the relationship. Specifically, we train a deep neural network to classify the coherent X-ray speckle pattern images according to the disk number density in the corresponding structure. It is demonstrated that the classification system is accurate for both non-disperse and disperse size distributions.
Combinatorial Black-Box Optimization with Expert Advice
Jun 06, 2020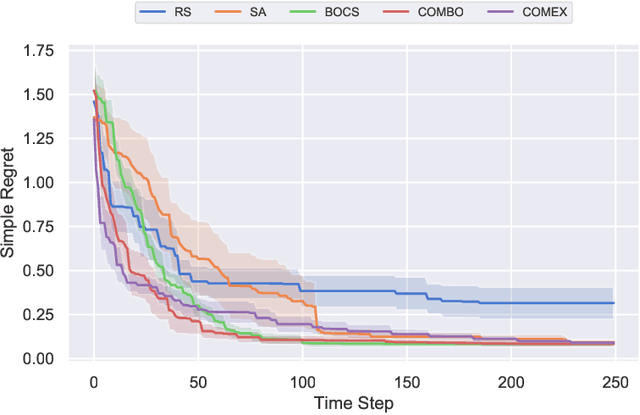
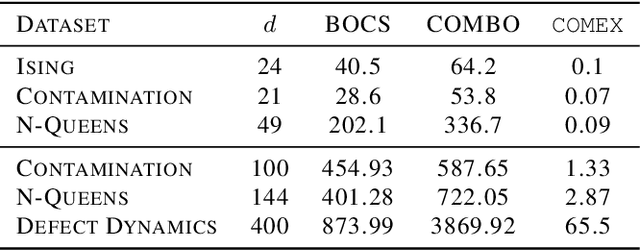
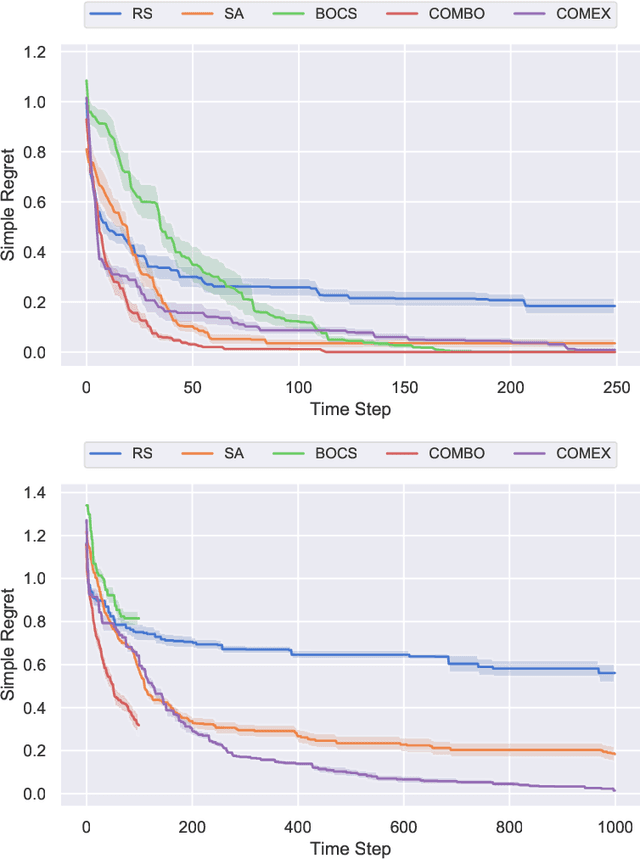
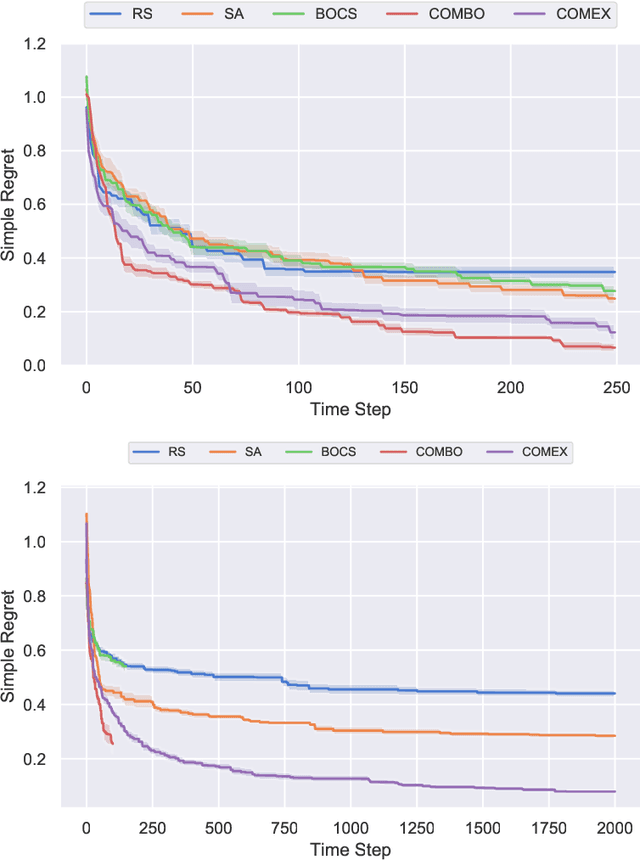
Abstract:We consider the problem of black-box function optimization over the boolean hypercube. Despite the vast literature on black-box function optimization over continuous domains, not much attention has been paid to learning models for optimization over combinatorial domains until recently. However, the computational complexity of the recently devised algorithms are prohibitive even for moderate numbers of variables; drawing one sample using the existing algorithms is more expensive than a function evaluation for many black-box functions of interest. To address this problem, we propose a computationally efficient model learning algorithm based on multilinear polynomials and exponential weight updates. In the proposed algorithm, we alternate between simulated annealing with respect to the current polynomial representation and updating the weights using monomial experts' advice. Numerical experiments on various datasets in both unconstrained and sum-constrained boolean optimization indicate the competitive performance of the proposed algorithm, while improving the computational time up to several orders of magnitude compared to state-of-the-art algorithms in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge