Soroosh Yazdani
MapTrace: Scalable Data Generation for Route Tracing on Maps
Dec 22, 2025Abstract:While Multimodal Large Language Models have achieved human-like performance on many visual and textual reasoning tasks, their proficiency in fine-grained spatial understanding, such as route tracing on maps remains limited. Unlike humans, who can quickly learn to parse and navigate maps, current models often fail to respect fundamental path constraints, in part due to the prohibitive cost and difficulty of collecting large-scale, pixel-accurate path annotations. To address this, we introduce a scalable synthetic data generation pipeline that leverages synthetic map images and pixel-level parsing to automatically produce precise annotations for this challenging task. Using this pipeline, we construct a fine-tuning dataset of 23k path samples across 4k maps, enabling models to acquire more human-like spatial capabilities. Using this dataset, we fine-tune both open-source and proprietary MLLMs. Results on MapBench show that finetuning substantially improves robustness, raising success rates by up to 6.4 points, while also reducing path-tracing error (NDTW). These gains highlight that fine-grained spatial reasoning, absent in pretrained models, can be explicitly taught with synthetic supervision.
NeuralBF: Neural Bilateral Filtering for Top-down Instance Segmentation on Point Clouds
Jul 20, 2022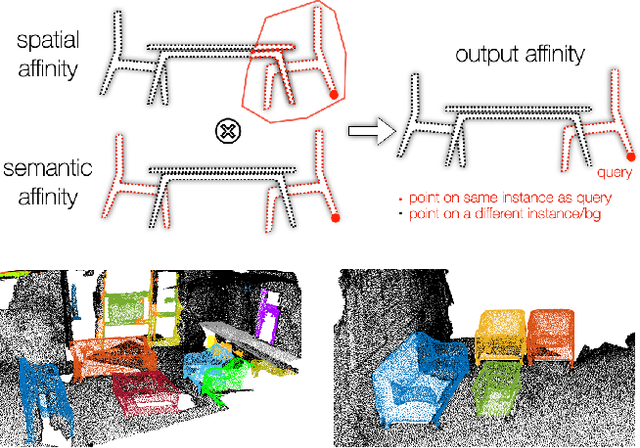
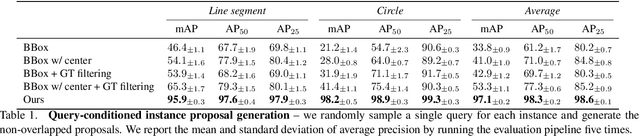
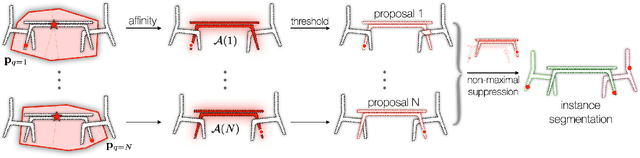
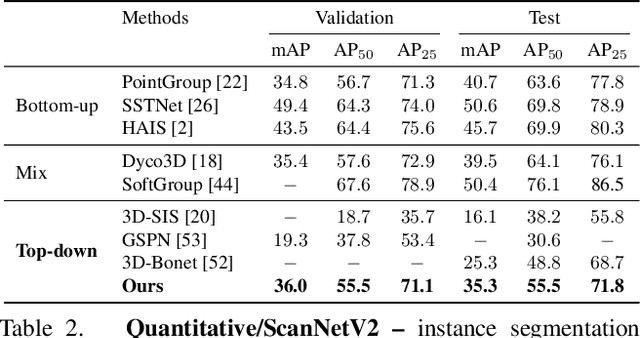
Abstract:We introduce a method for instance proposal generation for 3D point clouds. Existing techniques typically directly regress proposals in a single feed-forward step, leading to inaccurate estimation. We show that this serves as a critical bottleneck, and propose a method based on iterative bilateral filtering with learned kernels. Following the spirit of bilateral filtering, we consider both the deep feature embeddings of each point, as well as their locations in the 3D space. We show via synthetic experiments that our method brings drastic improvements when generating instance proposals for a given point of interest. We further validate our method on the challenging ScanNet benchmark, achieving the best instance segmentation performance amongst the sub-category of top-down methods.
Deep Medial Fields
Jun 07, 2021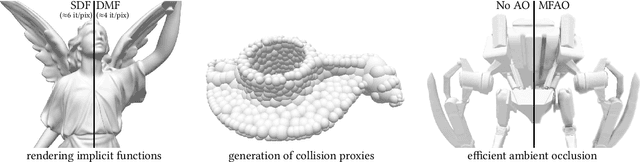
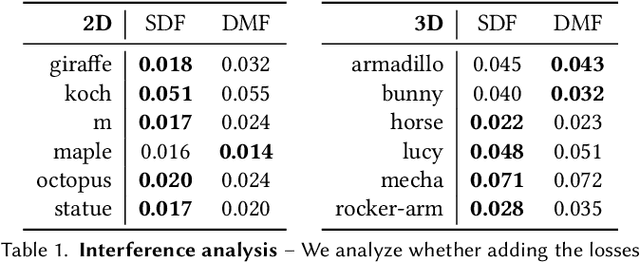
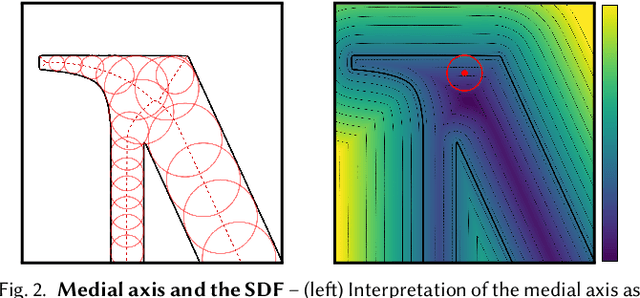

Abstract:Implicit representations of geometry, such as occupancy fields or signed distance fields (SDF), have recently re-gained popularity in encoding 3D solid shape in a functional form. In this work, we introduce medial fields: a field function derived from the medial axis transform (MAT) that makes available information about the underlying 3D geometry that is immediately useful for a number of downstream tasks. In particular, the medial field encodes the local thickness of a 3D shape, and enables O(1) projection of a query point onto the medial axis. To construct the medial field we require nothing but the SDF of the shape itself, thus allowing its straightforward incorporation in any application that relies on signed distance fields. Working in unison with the O(1) surface projection supported by the SDF, the medial field opens the door for an entirely new set of efficient, shape-aware operations on implicit representations. We present three such applications, including a modification to sphere tracing that renders implicit representations with better convergence properties, a fast construction method for memory-efficient rigid-body collision proxies, and an efficient approximation of ambient occlusion that remains stable with respect to viewpoint variations.
Canonical Capsules: Unsupervised Capsules in Canonical Pose
Dec 08, 2020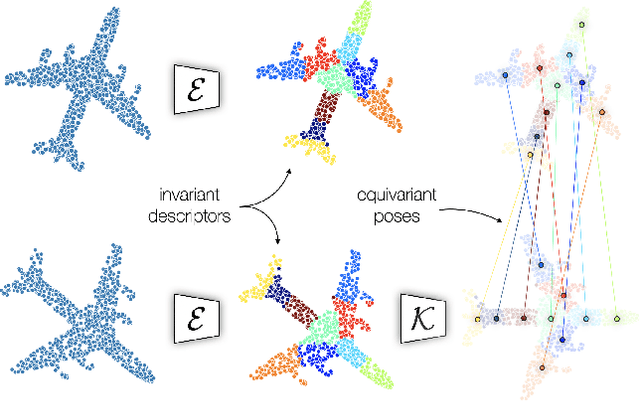
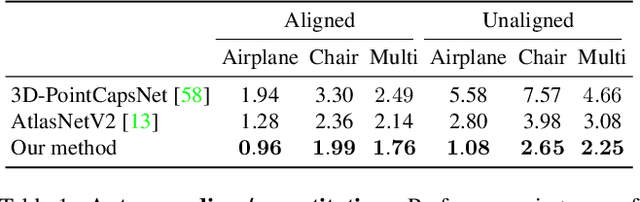

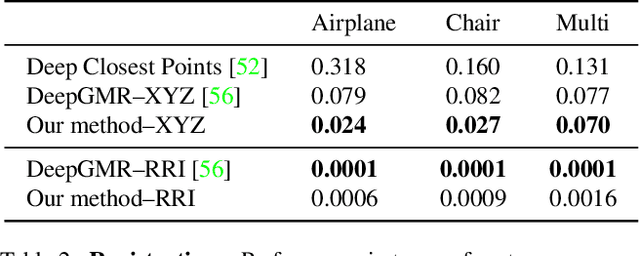
Abstract:We propose an unsupervised capsule architecture for 3D point clouds. We compute capsule decompositions of objects through permutation-equivariant attention, and self-supervise the process by training with pairs of randomly rotated objects. Our key idea is to aggregate the attention masks into semantic keypoints, and use these to supervise a decomposition that satisfies the capsule invariance/equivariance properties. This not only enables the training of a semantically consistent decomposition, but also allows us to learn a canonicalization operation that enables object-centric reasoning. In doing so, we require neither classification labels nor manually-aligned training datasets to train. Yet, by learning an object-centric representation in an unsupervised manner, our method outperforms the state-of-the-art on 3D point cloud reconstruction, registration, and unsupervised classification. We will release the code and dataset to reproduce our results as soon as the paper is published.
Unsupervised part representation by Flow Capsules
Nov 27, 2020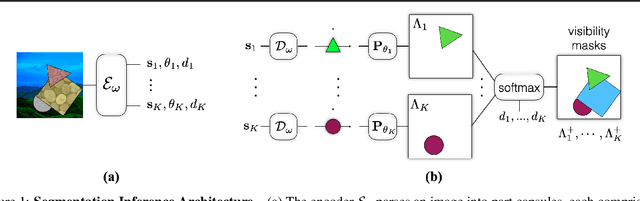
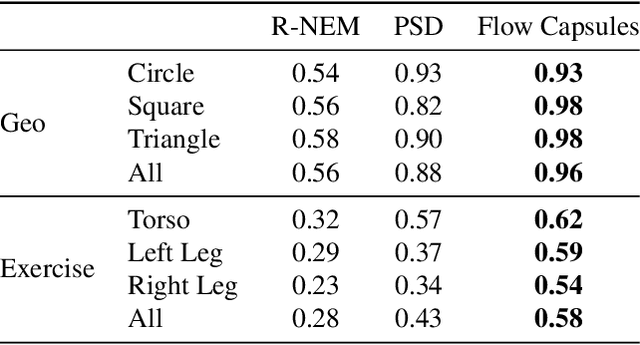

Abstract:Capsule networks are designed to parse an image into a hierarchy of objects, parts and relations. While promising, they remain limited by an inability to learn effective low level part descriptions. To address this issue we propose a novel self-supervised method for learning part descriptors of an image. During training, we exploit motion as a powerful perceptual cue for part definition, using an expressive decoder for part generation and layered image formation with occlusion. Experiments demonstrate robust part discovery in the presence of multiple objects, cluttered backgrounds, and significant occlusion. The resulting part descriptors, a.k.a. part capsules, are decoded into shape masks, filling in occluded pixels, along with relative depth on single images. We also report unsupervised object classification using our capsule parts in a stacked capsule autoencoder.
DeRF: Decomposed Radiance Fields
Nov 25, 2020
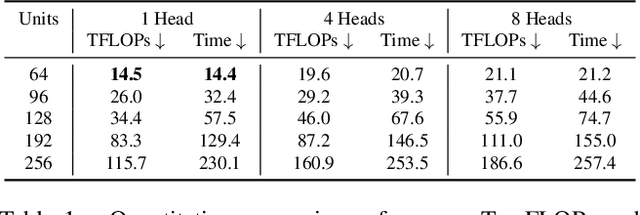
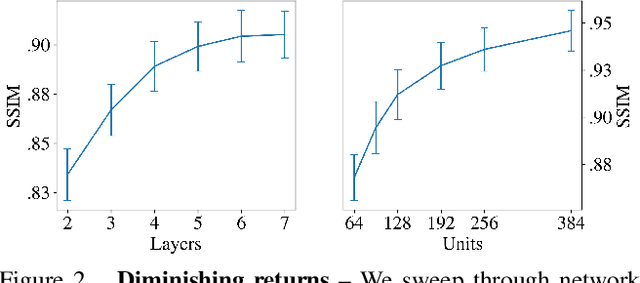
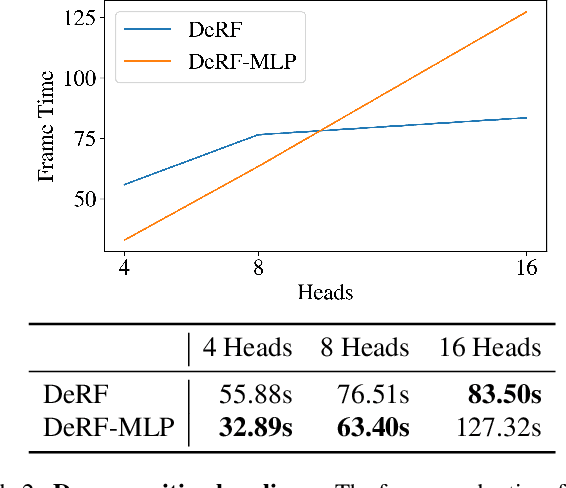
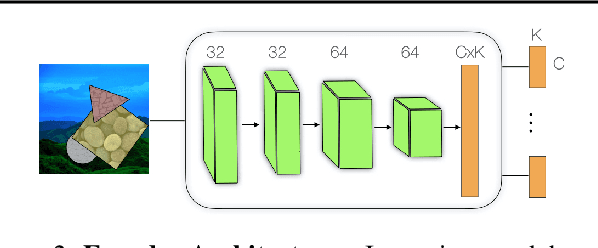
Abstract:With the advent of Neural Radiance Fields (NeRF), neural networks can now render novel views of a 3D scene with quality that fools the human eye. Yet, generating these images is very computationally intensive, limiting their applicability in practical scenarios. In this paper, we propose a technique based on spatial decomposition capable of mitigating this issue. Our key observation is that there are diminishing returns in employing larger (deeper and/or wider) networks. Hence, we propose to spatially decompose a scene and dedicate smaller networks for each decomposed part. When working together, these networks can render the whole scene. This allows us near-constant inference time regardless of the number of decomposed parts. Moreover, we show that a Voronoi spatial decomposition is preferable for this purpose, as it is provably compatible with the Painter's Algorithm for efficient and GPU-friendly rendering. Our experiments show that for real-world scenes, our method provides up to 3x more efficient inference than NeRF (with the same rendering quality), or an improvement of up to 1.0~dB in PSNR (for the same inference cost).
Voronoi Convolutional Neural Networks
Oct 21, 2020Abstract:In this technical report, we investigate extending convolutional neural networks to the setting where functions are not sampled in a grid pattern. We show that by treating the samples as the average of a function within a cell, we can find a natural equivalent of most layers used in CNN. We also present an algorithm for running inference for these models exactly using standard convex geometry algorithms.
CvxNets: Learnable Convex Decomposition
Sep 12, 2019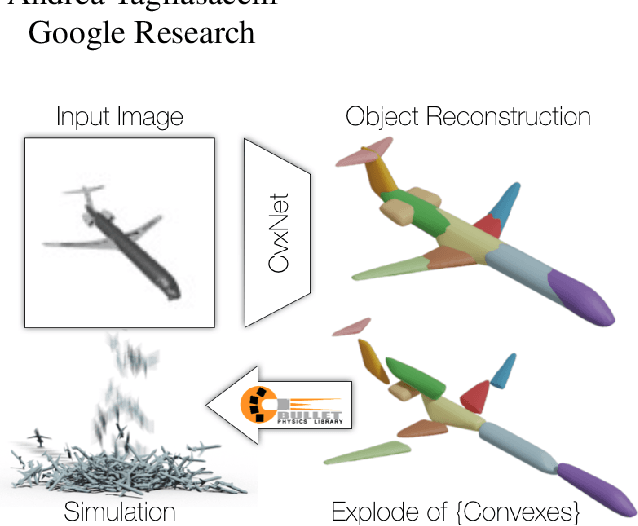
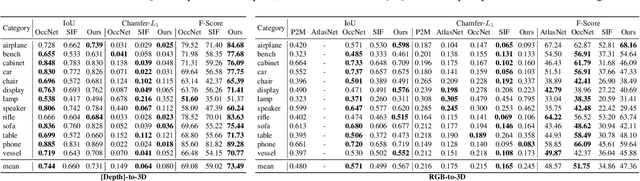
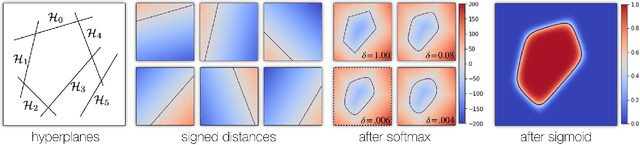
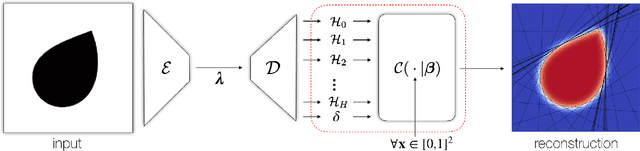
Abstract:Any solid object can be decomposed into a collection of convex polytopes (in short, convexes). When a small number of convexes are used, such a decomposition can be thought of as a piece-wise approximation of the geometry. This decomposition is fundamental to real-time physics simulation in computer graphics, where it creates a unifying representation of dynamic geometry for collision detection. A convex object also has the property of being simultaneously an explicit and implicit representation: one can interpret it explicitly as a mesh derived by computing the vertices of a convex hull, or implicitly as the collection of half-space constraints or support functions. Their implicit representation makes them particularly well suited for neural network training, as they abstract away from the topology of the geometry they need to represent. We introduce a network architecture to represent a low dimensional family of convexes. This family is automatically derived via an autoencoding process. We investigate the applications of the network including automatic convex decomposition, image to 3D reconstruction, and part-based shape retrieval.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge