Deep Medial Fields
Paper and Code
Jun 07, 2021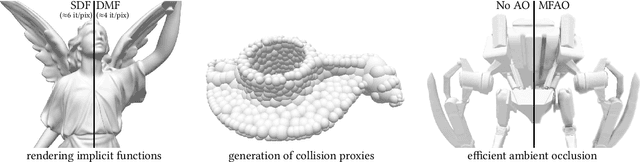
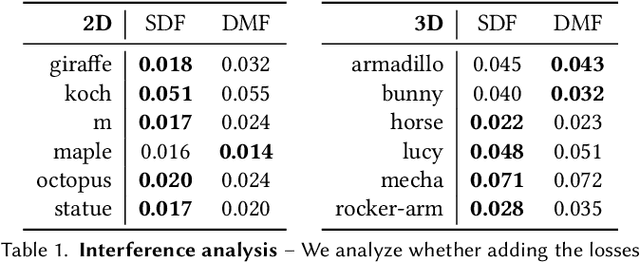
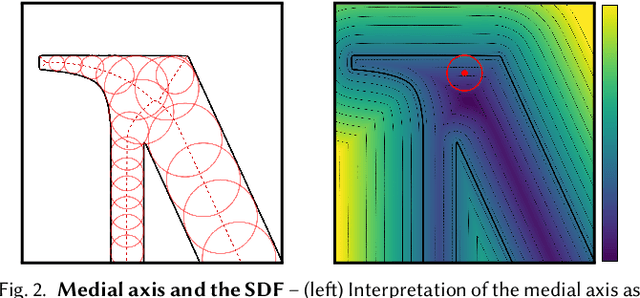

Implicit representations of geometry, such as occupancy fields or signed distance fields (SDF), have recently re-gained popularity in encoding 3D solid shape in a functional form. In this work, we introduce medial fields: a field function derived from the medial axis transform (MAT) that makes available information about the underlying 3D geometry that is immediately useful for a number of downstream tasks. In particular, the medial field encodes the local thickness of a 3D shape, and enables O(1) projection of a query point onto the medial axis. To construct the medial field we require nothing but the SDF of the shape itself, thus allowing its straightforward incorporation in any application that relies on signed distance fields. Working in unison with the O(1) surface projection supported by the SDF, the medial field opens the door for an entirely new set of efficient, shape-aware operations on implicit representations. We present three such applications, including a modification to sphere tracing that renders implicit representations with better convergence properties, a fast construction method for memory-efficient rigid-body collision proxies, and an efficient approximation of ambient occlusion that remains stable with respect to viewpoint variations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge