Multi-disciplinary fairness considerations in machine learning for clinical trials

While interest in the application of machine learning to improve healthcare has grown tremendously in recent years, a number of barriers prevent deployment in medical practice. A notable concern is the potential to exacerbate entrenched biases and existing health disparities in society. The area of fairness in machine learning seeks to address these issues of equity; however, appropriate approaches are context-dependent, necessitating domain-specific consideration. We focus on clinical trials, i.e., research studies conducted on humans to evaluate medical treatments. Clinical trials are a relatively under-explored application in machine learning for healthcare, in part due to complex ethical, legal, and regulatory requirements and high costs. Our aim is to provide a multi-disciplinary assessment of how fairness for machine learning fits into the context of clinical trials research and practice. We start by reviewing the current ethical considerations and guidelines for clinical trials and examine their relationship with common definitions of fairness in machine learning. We examine potential sources of unfairness in clinical trials, providing concrete examples, and discuss the role machine learning might play in either mitigating potential biases or exacerbating them when applied without care. Particular focus is given to adaptive clinical trials, which may employ machine learning. Finally, we highlight concepts that require further investigation and development, and emphasize new approaches to fairness that may be relevant to the design of clinical trials.

Some performance considerations when using multi-armed bandit algorithms in the presence of missing data

When using multi-armed bandit algorithms, the potential impact of missing data is often overlooked. In practice, the simplest approach is to ignore missing outcomes and continue to sample following the bandit algorithm. We investigate the impact of missing data on several bandit algorithms via a simulation study assuming the rewards are missing at random. We focus on two-armed bandit algorithms with binary outcomes in the context of patient allocation for clinical trials with relatively small sample sizes. However, our results can apply to other applications of bandit algorithms where missing data is expected to occur. We assess the resulting operating characteristics, including the expected reward (i.e., allocation results). Different probabilities of missingness in both arms are considered. The key finding of our work is that when using the simplest strategy of ignoring missing data, the corresponding impact on the performance of multi-armed bandit strategies varies according to their way of balancing the exploration-exploitation trade-off. Algorithms that are geared towards exploration continue to assign samples to the arm with more missing responses, and this arm is perceived as the superior arm by the algorithm. By contrast, algorithms that are geared towards exploitation would do the opposite and not assign samples to the arms with more missing responses. Furthermore, for algorithms focusing more on exploration, we illustrate that the problem of missing responses can be alleviated using a simple mean imputation approach.

Algorithms for Adaptive Experiments that Trade-off Statistical Analysis with Reward: Combining Uniform Random Assignment and Reward Maximization

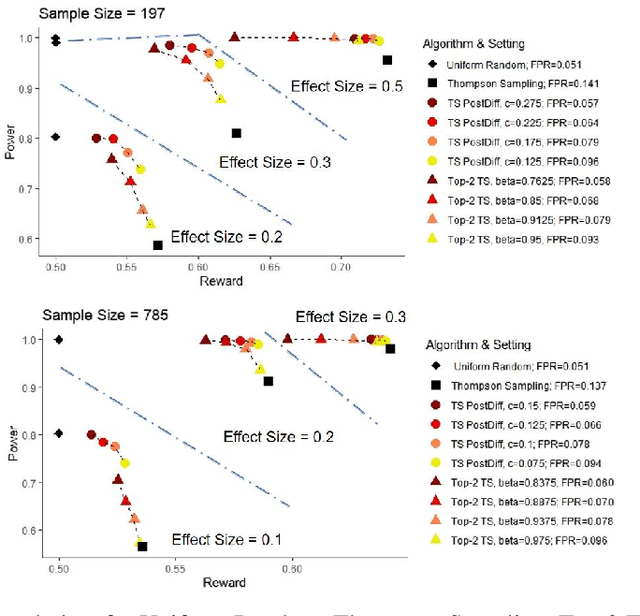
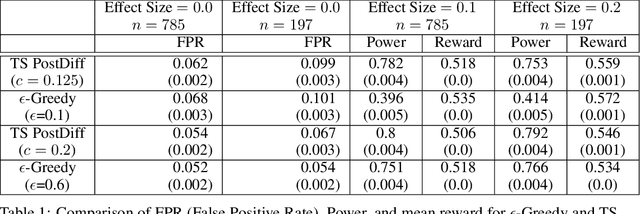
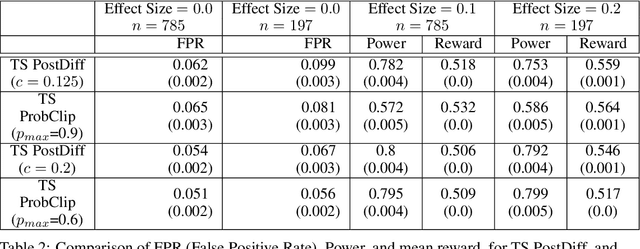
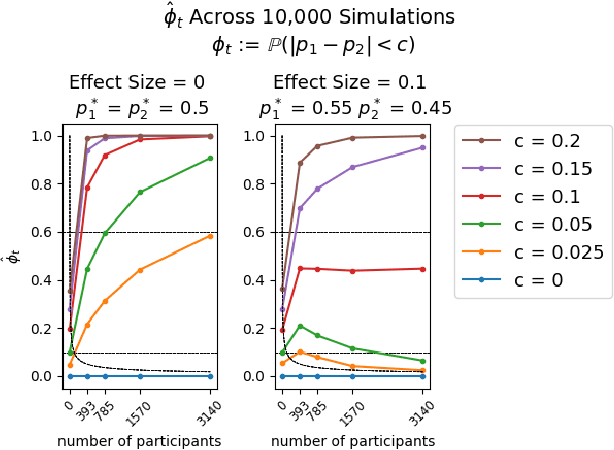
Multi-armed bandit algorithms like Thompson Sampling can be used to conduct adaptive experiments, in which maximizing reward means that data is used to progressively assign more participants to more effective arms. Such assignment strategies increase the risk of statistical hypothesis tests identifying a difference between arms when there is not one, and failing to conclude there is a difference in arms when there truly is one. We present simulations for 2-arm experiments that explore two algorithms that combine the benefits of uniform randomization for statistical analysis, with the benefits of reward maximization achieved by Thompson Sampling (TS). First, Top-Two Thompson Sampling adds a fixed amount of uniform random allocation (UR) spread evenly over time. Second, a novel heuristic algorithm, called TS PostDiff (Posterior Probability of Difference). TS PostDiff takes a Bayesian approach to mixing TS and UR: the probability a participant is assigned using UR allocation is the posterior probability that the difference between two arms is `small' (below a certain threshold), allowing for more UR exploration when there is little or no reward to be gained. We find that TS PostDiff method performs well across multiple effect sizes, and thus does not require tuning based on a guess for the true effect size.

Efficient Inference Without Trading-off Regret in Bandits: An Allocation Probability Test for Thompson Sampling

Using bandit algorithms to conduct adaptive randomised experiments can minimise regret, but it poses major challenges for statistical inference (e.g., biased estimators, inflated type-I error and reduced power). Recent attempts to address these challenges typically impose restrictions on the exploitative nature of the bandit algorithm$-$trading off regret$-$and require large sample sizes to ensure asymptotic guarantees. However, large experiments generally follow a successful pilot study, which is tightly constrained in its size or duration. Increasing power in such small pilot experiments, without limiting the adaptive nature of the algorithm, can allow promising interventions to reach a larger experimental phase. In this work we introduce a novel hypothesis test, uniquely based on the allocation probabilities of the bandit algorithm, and without constraining its exploitative nature or requiring a minimum experimental size. We characterise our $Allocation\ Probability\ Test$ when applied to $Thompson\ Sampling$, presenting its asymptotic theoretical properties, and illustrating its finite-sample performances compared to state-of-the-art approaches. We demonstrate the regret and inferential advantages of our approach, particularly in small samples, in both extensive simulations and in a real-world experiment on mental health aspects.

Challenges in Statistical Analysis of Data Collected by a Bandit Algorithm: An Empirical Exploration in Applications to Adaptively Randomized Experiments

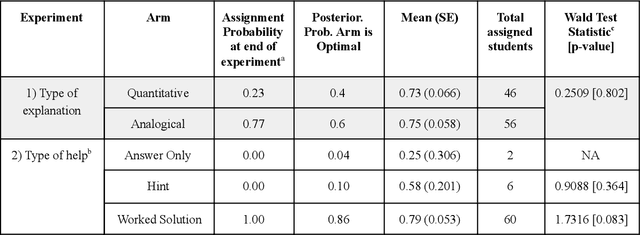
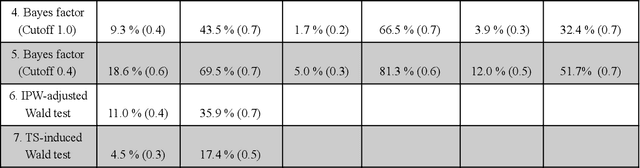
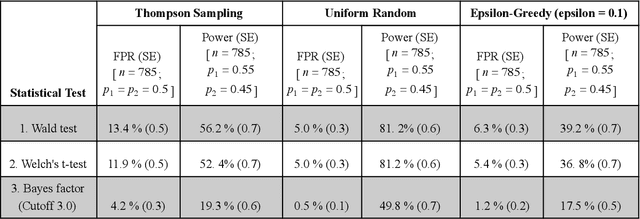
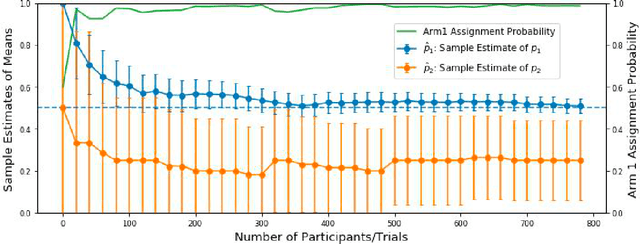
Multi-armed bandit algorithms have been argued for decades as useful for adaptively randomized experiments. In such experiments, an algorithm varies which arms (e.g. alternative interventions to help students learn) are assigned to participants, with the goal of assigning higher-reward arms to as many participants as possible. We applied the bandit algorithm Thompson Sampling (TS) to run adaptive experiments in three university classes. Instructors saw great value in trying to rapidly use data to give their students in the experiments better arms (e.g. better explanations of a concept). Our deployment, however, illustrated a major barrier for scientists and practitioners to use such adaptive experiments: a lack of quantifiable insight into how much statistical analysis of specific real-world experiments is impacted (Pallmann et al, 2018; FDA, 2019), compared to traditional uniform random assignment. We therefore use our case study of the ubiquitous two-arm binary reward setting to empirically investigate the impact of using Thompson Sampling instead of uniform random assignment. In this setting, using common statistical hypothesis tests, we show that collecting data with TS can as much as double the False Positive Rate (FPR; incorrectly reporting differences when none exist) and the False Negative Rate (FNR; failing to report differences when they exist)...

Learning for Dose Allocation in Adaptive Clinical Trials with Safety Constraints

Phase I dose-finding trials are increasingly challenging as the relationship between efficacy and toxicity of new compounds (or combination of them) becomes more complex. Despite this, most commonly used methods in practice focus on identifying a Maximum Tolerated Dose (MTD) by learning only from toxicity events. We present a novel adaptive clinical trial methodology, called Safe Efficacy Exploration Dose Allocation (SEEDA), that aims at maximizing the cumulative efficacies while satisfying the toxicity safety constraint with high probability. We evaluate performance objectives that have operational meanings in practical clinical trials, including cumulative efficacy, recommendation/allocation success probabilities, toxicity violation probability, and sample efficiency. An extended SEEDA-Plateau algorithm that is tailored for the increase-then-plateau efficacy behavior of molecularly targeted agents (MTA) is also presented. Through numerical experiments using both synthetic and real-world datasets, we show that SEEDA outperforms state-of-the-art clinical trial designs by finding the optimal dose with higher success rate and fewer patients.