Three-Player Game Training Dynamics

This work explores three-player game training dynamics, under what conditions three-player games converge and the equilibria the converge on. In contrast to prior work, we examine a three-player game architecture in which all players explicitly interact with each other. Prior work analyzes games in which two of three agents interact with only one other player, constituting dual two-player games. We explore three-player game training dynamics using an extended version of a simplified bilinear smooth game, called a simplified trilinear smooth game. We find that trilinear games do not converge on the Nash equilibrium in most cases, rather converging on a fixed point which is optimal for two players, but not for the third. Further, we explore how the order of the updates influences convergence. In addition to alternating and simultaneous updates, we explore a new update order--maximizer-first--which is only possible in a three-player game. We find that three-player games can converge on a Nash equilibrium using maximizer-first updates. Finally, we experiment with differing momentum values for each player in a trilinear smooth game under all three update orders and show that maximizer-first updates achieve more optimal results in a larger set of player-specific momentum value triads than other update orders.

Increasing Students' Engagement to Reminder Emails Through Multi-Armed Bandits

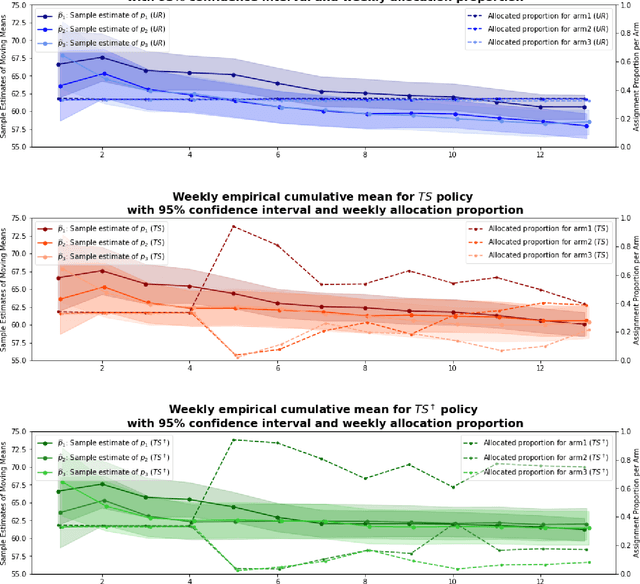
Conducting randomized experiments in education settings raises the question of how we can use machine learning techniques to improve educational interventions. Using Multi-Armed Bandits (MAB) algorithms like Thompson Sampling (TS) in adaptive experiments can increase students' chances of obtaining better outcomes by increasing the probability of assignment to the most optimal condition (arm), even before an intervention completes. This is an advantage over traditional A/B testing, which may allocate an equal number of students to both optimal and non-optimal conditions. The problem is the exploration-exploitation trade-off. Even though adaptive policies aim to collect enough information to allocate more students to better arms reliably, past work shows that this may not be enough exploration to draw reliable conclusions about whether arms differ. Hence, it is of interest to provide additional uniform random (UR) exploration throughout the experiment. This paper shows a real-world adaptive experiment on how students engage with instructors' weekly email reminders to build their time management habits. Our metric of interest is open email rates which tracks the arms represented by different subject lines. These are delivered following different allocation algorithms: UR, TS, and what we identified as TS{\dag} - which combines both TS and UR rewards to update its priors. We highlight problems with these adaptive algorithms - such as possible exploitation of an arm when there is no significant difference - and address their causes and consequences. Future directions includes studying situations where the early choice of the optimal arm is not ideal and how adaptive algorithms can address them.

Algorithms for Adaptive Experiments that Trade-off Statistical Analysis with Reward: Combining Uniform Random Assignment and Reward Maximization

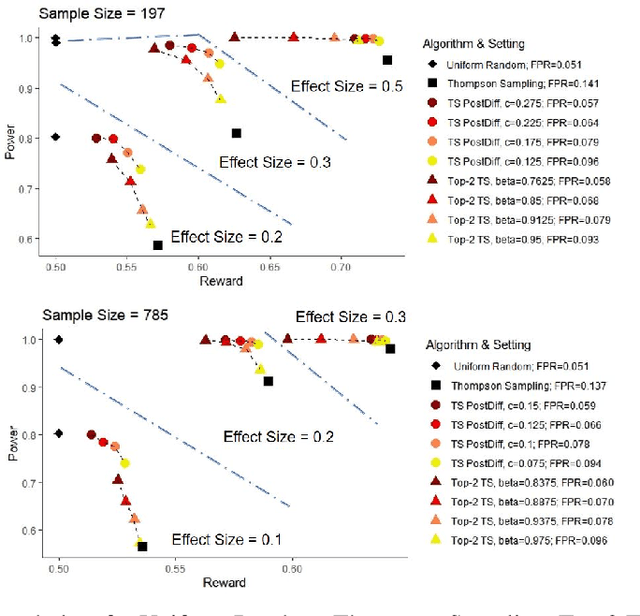
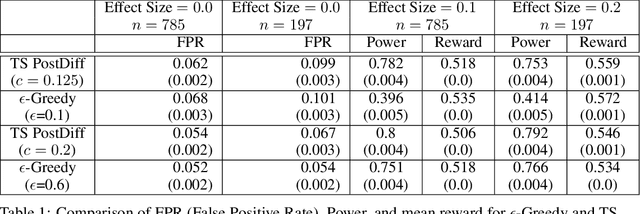
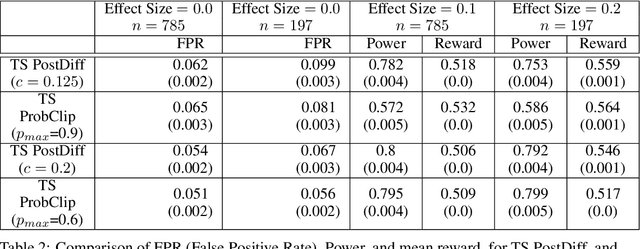
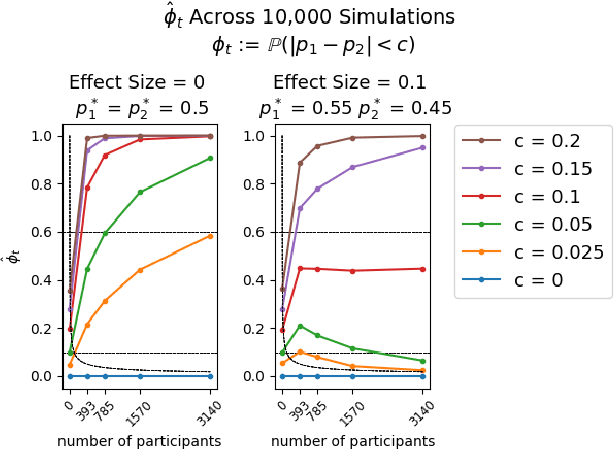
Multi-armed bandit algorithms like Thompson Sampling can be used to conduct adaptive experiments, in which maximizing reward means that data is used to progressively assign more participants to more effective arms. Such assignment strategies increase the risk of statistical hypothesis tests identifying a difference between arms when there is not one, and failing to conclude there is a difference in arms when there truly is one. We present simulations for 2-arm experiments that explore two algorithms that combine the benefits of uniform randomization for statistical analysis, with the benefits of reward maximization achieved by Thompson Sampling (TS). First, Top-Two Thompson Sampling adds a fixed amount of uniform random allocation (UR) spread evenly over time. Second, a novel heuristic algorithm, called TS PostDiff (Posterior Probability of Difference). TS PostDiff takes a Bayesian approach to mixing TS and UR: the probability a participant is assigned using UR allocation is the posterior probability that the difference between two arms is `small' (below a certain threshold), allowing for more UR exploration when there is little or no reward to be gained. We find that TS PostDiff method performs well across multiple effect sizes, and thus does not require tuning based on a guess for the true effect size.