Deep Learning Based Object Tracking in Walking Droplet and Granular Intruder Experiments

We present a deep-learning based tracking objects of interest in walking droplet and granular intruder experiments. In a typical walking droplet experiment, a liquid droplet, known as \textit{walker}, propels itself laterally on the free surface of a vibrating bath of the same liquid. This motion is the result of the interaction between the droplets and the surface waves generated by the droplet itself after each successive bounce. A walker can exhibit a highly irregular trajectory over the course of its motion, including rapid acceleration and complex interactions with the other walkers present in the same bath. In analogy with the hydrodynamic experiments, the granular matter experiments consist of a vibrating bath of very small solid particles and a larger solid \textit{intruder}. Like the fluid droplets, the intruder interacts with and travels the domain due to the waves of the bath but tends to move much slower and much less smoothly than the droplets. When multiple intruders are introduced, they also exhibit complex interactions with each other. We leverage the state-of-art object detection model YOLO and the Hungarian Algorithm to accurately extract the trajectory of a walker or intruder in real-time. Our proposed methodology is capable of tracking individual walker(s) or intruder(s) in digital images acquired from a broad spectrum of experimental settings and does not suffer from any identity-switch issues. Thus, the deep learning approach developed in this work could be used to automatize the efficient, fast and accurate extraction of observables of interests in walking droplet and granular flow experiments. Such extraction capabilities are critically enabling for downstream tasks such as building data-driven dynamical models for the coarse-grained dynamics and interactions of the objects of interest.

Algorithms for Adaptive Experiments that Trade-off Statistical Analysis with Reward: Combining Uniform Random Assignment and Reward Maximization

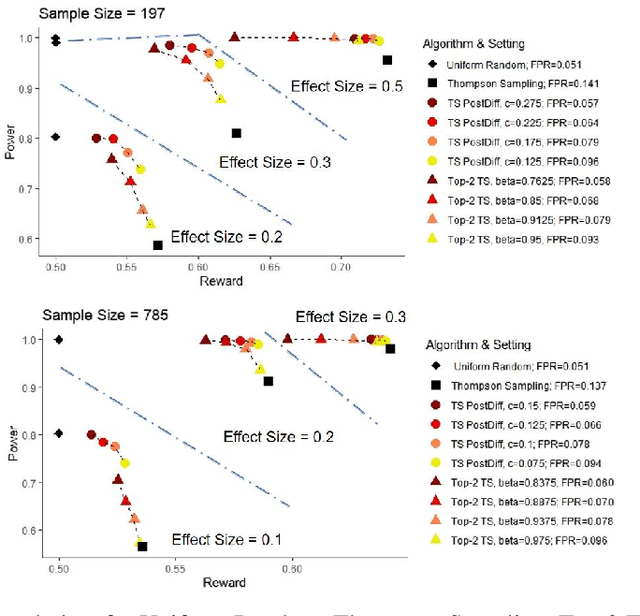
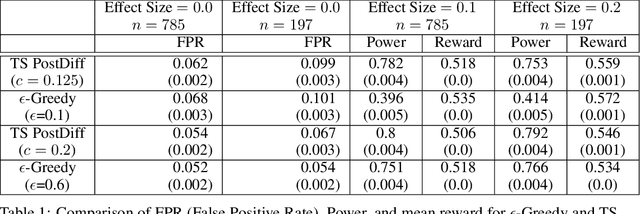
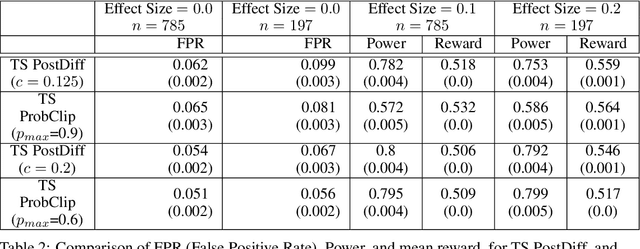
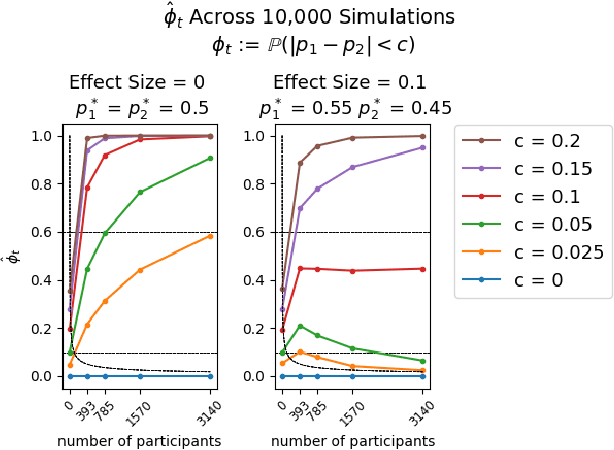
Multi-armed bandit algorithms like Thompson Sampling can be used to conduct adaptive experiments, in which maximizing reward means that data is used to progressively assign more participants to more effective arms. Such assignment strategies increase the risk of statistical hypothesis tests identifying a difference between arms when there is not one, and failing to conclude there is a difference in arms when there truly is one. We present simulations for 2-arm experiments that explore two algorithms that combine the benefits of uniform randomization for statistical analysis, with the benefits of reward maximization achieved by Thompson Sampling (TS). First, Top-Two Thompson Sampling adds a fixed amount of uniform random allocation (UR) spread evenly over time. Second, a novel heuristic algorithm, called TS PostDiff (Posterior Probability of Difference). TS PostDiff takes a Bayesian approach to mixing TS and UR: the probability a participant is assigned using UR allocation is the posterior probability that the difference between two arms is `small' (below a certain threshold), allowing for more UR exploration when there is little or no reward to be gained. We find that TS PostDiff method performs well across multiple effect sizes, and thus does not require tuning based on a guess for the true effect size.

Efficient Inference Without Trading-off Regret in Bandits: An Allocation Probability Test for Thompson Sampling

Using bandit algorithms to conduct adaptive randomised experiments can minimise regret, but it poses major challenges for statistical inference (e.g., biased estimators, inflated type-I error and reduced power). Recent attempts to address these challenges typically impose restrictions on the exploitative nature of the bandit algorithm$-$trading off regret$-$and require large sample sizes to ensure asymptotic guarantees. However, large experiments generally follow a successful pilot study, which is tightly constrained in its size or duration. Increasing power in such small pilot experiments, without limiting the adaptive nature of the algorithm, can allow promising interventions to reach a larger experimental phase. In this work we introduce a novel hypothesis test, uniquely based on the allocation probabilities of the bandit algorithm, and without constraining its exploitative nature or requiring a minimum experimental size. We characterise our $Allocation\ Probability\ Test$ when applied to $Thompson\ Sampling$, presenting its asymptotic theoretical properties, and illustrating its finite-sample performances compared to state-of-the-art approaches. We demonstrate the regret and inferential advantages of our approach, particularly in small samples, in both extensive simulations and in a real-world experiment on mental health aspects.