Deep Learning Based Object Tracking in Walking Droplet and Granular Intruder Experiments

We present a deep-learning based tracking objects of interest in walking droplet and granular intruder experiments. In a typical walking droplet experiment, a liquid droplet, known as \textit{walker}, propels itself laterally on the free surface of a vibrating bath of the same liquid. This motion is the result of the interaction between the droplets and the surface waves generated by the droplet itself after each successive bounce. A walker can exhibit a highly irregular trajectory over the course of its motion, including rapid acceleration and complex interactions with the other walkers present in the same bath. In analogy with the hydrodynamic experiments, the granular matter experiments consist of a vibrating bath of very small solid particles and a larger solid \textit{intruder}. Like the fluid droplets, the intruder interacts with and travels the domain due to the waves of the bath but tends to move much slower and much less smoothly than the droplets. When multiple intruders are introduced, they also exhibit complex interactions with each other. We leverage the state-of-art object detection model YOLO and the Hungarian Algorithm to accurately extract the trajectory of a walker or intruder in real-time. Our proposed methodology is capable of tracking individual walker(s) or intruder(s) in digital images acquired from a broad spectrum of experimental settings and does not suffer from any identity-switch issues. Thus, the deep learning approach developed in this work could be used to automatize the efficient, fast and accurate extraction of observables of interests in walking droplet and granular flow experiments. Such extraction capabilities are critically enabling for downstream tasks such as building data-driven dynamical models for the coarse-grained dynamics and interactions of the objects of interest.

Universal Rate-Distortion-Perception Representations for Lossy Compression

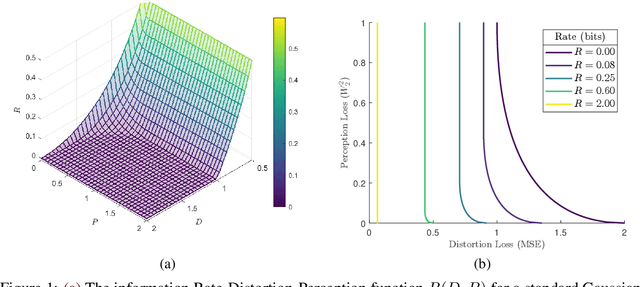
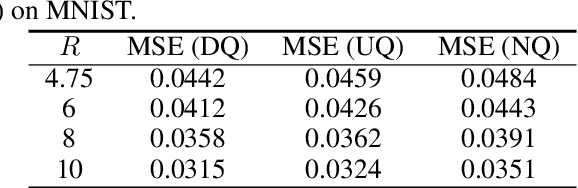
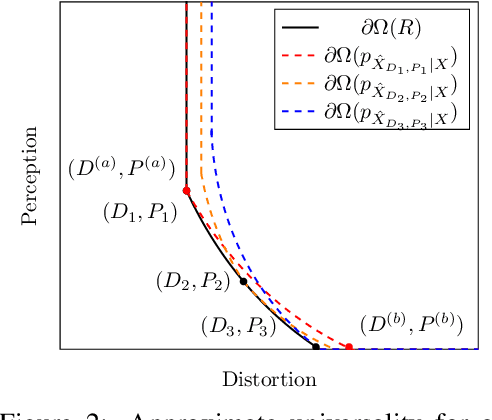
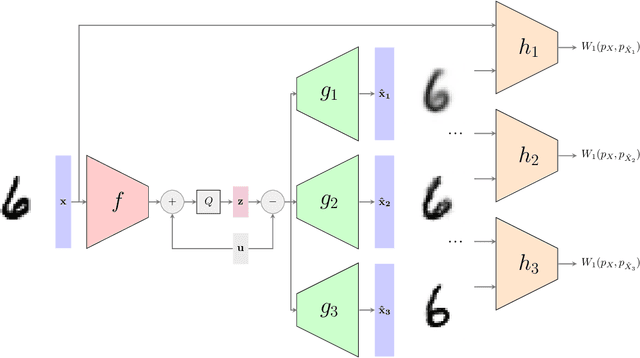
In the context of lossy compression, Blau & Michaeli (2019) adopt a mathematical notion of perceptual quality and define the information rate-distortion-perception function, generalizing the classical rate-distortion tradeoff. We consider the notion of universal representations in which one may fix an encoder and vary the decoder to achieve any point within a collection of distortion and perception constraints. We prove that the corresponding information-theoretic universal rate-distortion-perception function is operationally achievable in an approximate sense. Under MSE distortion, we show that the entire distortion-perception tradeoff of a Gaussian source can be achieved by a single encoder of the same rate asymptotically. We then characterize the achievable distortion-perception region for a fixed representation in the case of arbitrary distributions, identify conditions under which the aforementioned results continue to hold approximately, and study the case when the rate is not fixed in advance. This motivates the study of practical constructions that are approximately universal across the RDP tradeoff, thereby alleviating the need to design a new encoder for each objective. We provide experimental results on MNIST and SVHN suggesting that on image compression tasks, the operational tradeoffs achieved by machine learning models with a fixed encoder suffer only a small penalty when compared to their variable encoder counterparts.