Global Contact-Rich Planning with Sparsity-Rich Semidefinite Relaxations

We show that contact-rich motion planning is also sparsity-rich when viewed as polynomial optimization (POP). We can exploit not only the correlative and term sparsity patterns that are general to all POPs, but also specialized sparsity patterns from the robot kinematic structure and the separability of contact modes. Such sparsity enables the design of high-order but sparse semidefinite programming (SDPs) relaxations--building upon Lasserre's moment and sums of squares hierarchy--that (i) can be solved in seconds by off-the-shelf SDP solvers, and (ii) compute near globally optimal solutions to the nonconvex contact-rich planning problems with small certified suboptimality. Through extensive experiments both in simulation (Push Bot, Push Box, Push Box with Obstacles, and Planar Hand) and real world (Push T), we demonstrate the power of using convex SDP relaxations to generate global contact-rich motion plans. As a contribution of independent interest, we release the Sparse Polynomial Optimization Toolbox (SPOT)--implemented in C++ with interfaces to both Python and Matlab--that automates sparsity exploitation for robotics and beyond.

On the Surprising Robustness of Sequential Convex Optimization for Contact-Implicit Motion Planning

Contact-implicit motion planning-embedding contact sequencing as implicit complementarity constraints-holds the promise of leveraging continuous optimization to discover new contact patterns online. Nevertheless, the resulting optimization, being an instance of Mathematical Programming with Complementary Constraints, fails the classical constraint qualifications that are crucial for the convergence of popular numerical solvers. We present robust contact-implicit motion planning with sequential convex programming (CRISP), a solver that departs from the usual primal-dual algorithmic framework but instead only focuses on the primal problem. CRISP solves a convex quadratic program with an adaptive trust region radius at each iteration, and its convergence is evaluated by a merit function using weighted penalty. We (i) provide sufficient conditions on CRISP's convergence to first-order stationary points of the merit function; (ii) release a high-performance C++ implementation of CRISP with a generic nonlinear programming interface; and (iii) demonstrate CRISP's surprising robustness in solving contact-implicit planning with naive initialization. In fact, CRISP solves several contact-implicit problems with all-zero initialization.

Fast and Certifiable Trajectory Optimization

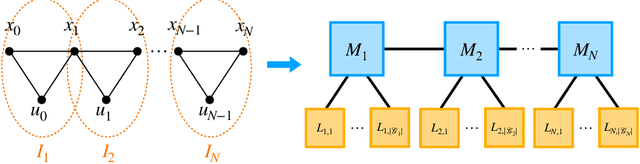
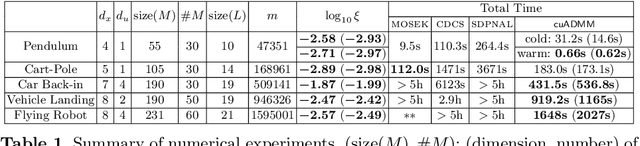
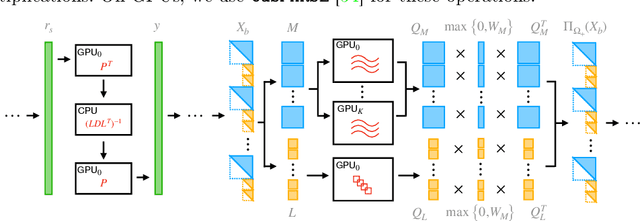
We propose semidefinite trajectory optimization (STROM), a framework that computes fast and certifiably optimal solutions for nonconvex trajectory optimization problems defined by polynomial objectives and constraints. STROM employs sparse second-order Lasserre's hierarchy to generate semidefinite program (SDP) relaxations of trajectory optimization. Different from existing tools (e.g., YALMIP and SOSTOOLS in Matlab), STROM generates chain-like multiple-block SDPs with only positive semidefinite (PSD) variables. Moreover, STROM does so two orders of magnitude faster. Underpinning STROM is cuADMM, the first ADMM-based SDP solver implemented in CUDA and runs in GPUs. cuADMM builds upon the symmetric Gauss-Seidel ADMM algorithm and leverages GPU parallelization to speedup solving sparse linear systems and projecting onto PSD cones. In five trajectory optimization problems (inverted pendulum, cart-pole, vehicle landing, flying robot, and car back-in), cuADMM computes optimal trajectories (with certified suboptimality below 1%) in minutes (when other solvers take hours or run out of memory) and seconds (when others take minutes). Further, when warmstarted by data-driven initialization in the inverted pendulum problem, cuADMM delivers real-time performance: providing certifiably optimal trajectories in 0.66 seconds despite the SDP has 49,500 variables and 47,351 constraints.

Zero-shot Transferable and Persistently Feasible Safe Control for High Dimensional Systems by Consistent Abstraction

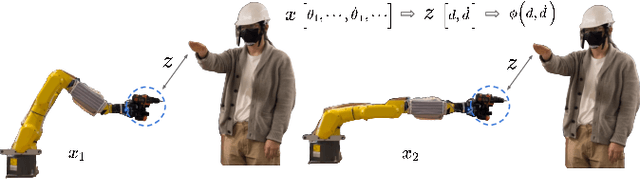
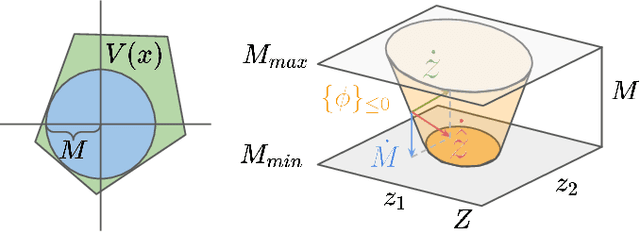
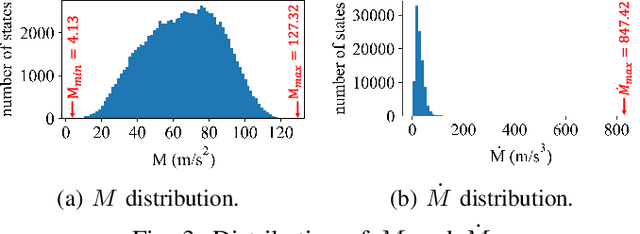
Safety is critical in robotic tasks. Energy function based methods have been introduced to address the problem. To ensure safety in the presence of control limits, we need to design an energy function that results in persistently feasible safe control at all system states. However, designing such an energy function for high-dimensional nonlinear systems remains challenging. Considering the fact that there are redundant dynamics in high dimensional systems with respect to the safety specifications, this paper proposes a novel approach called abstract safe control. We propose a system abstraction method that enables the design of energy functions on a low-dimensional model. Then we can synthesize the energy function with respect to the low-dimensional model to ensure persistent feasibility. The resulting safe controller can be directly transferred to other systems with the same abstraction, e.g., when a robot arm holds different tools. The proposed approach is demonstrated on a 7-DoF robot arm (14 states) both in simulation and real-world. Our method always finds feasible control and achieves zero safety violations in 500 trials on 5 different systems.

Verification and Synthesis of Robust Control Barrier Functions: Multilevel Polynomial Optimization and Semidefinite Relaxation

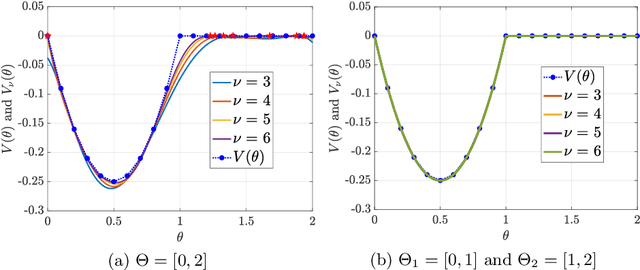
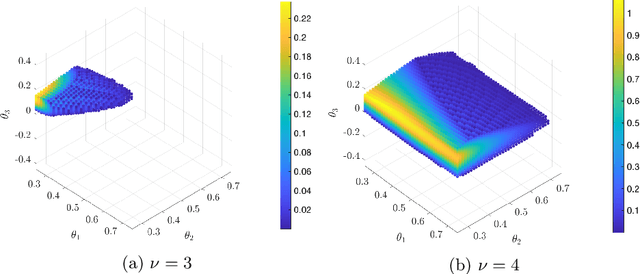
We study the problem of verification and synthesis of robust control barrier functions (CBF) for control-affine polynomial systems with bounded additive uncertainty and convex polynomial constraints on the control. We first formulate robust CBF verification and synthesis as multilevel polynomial optimization problems (POP), where verification optimizes -- in three levels -- the uncertainty, control, and state, while synthesis additionally optimizes the parameter of a chosen parametric CBF candidate. We then show that, by invoking the KKT conditions of the inner optimizations over uncertainty and control, the verification problem can be simplified as a single-level POP and the synthesis problem reduces to a min-max POP. This reduction leads to multilevel semidefinite relaxations. For the verification problem, we apply Lasserre's hierarchy of moment relaxations. For the synthesis problem, we draw connections to existing relaxation techniques for robust min-max POP, which first use sum-of-squares programming to find increasingly tight polynomial lower bounds to the unknown value function of the verification POP, and then call Lasserre's hierarchy again to maximize the lower bounds. Both semidefinite relaxations guarantee asymptotic global convergence to optimality. We provide an in-depth study of our framework on the controlled Van der Pol Oscillator, both with and without additive uncertainty.

Robust Safe Control for Uncertain Dynamic Models

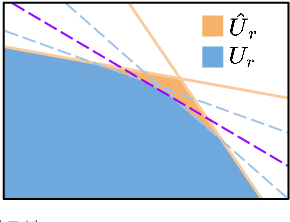
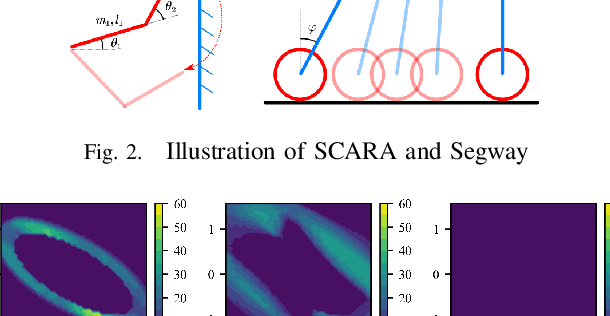
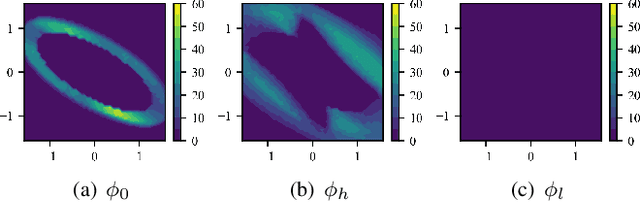
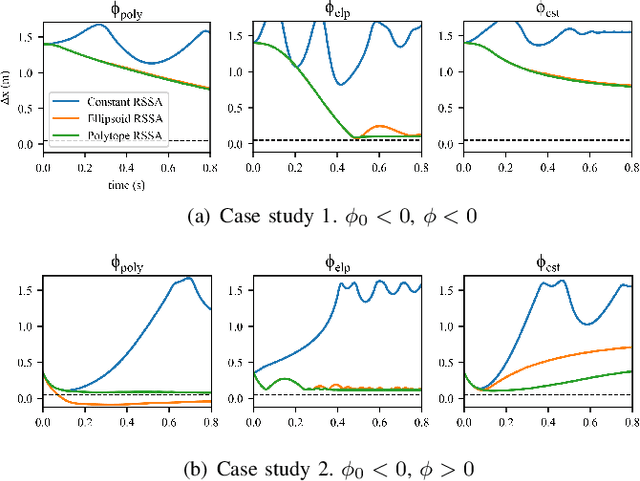
Model mismatches prevail in real-world applications. Hence it is important to design robust safe control algorithms for systems with uncertain dynamic models. The major challenge is that uncertainty results in difficulty in finding a feasible safe control in real-time. Existing methods usually simplify the problem such as restricting uncertainty type, ignoring control limits, or forgoing feasibility guarantees. In this work, we overcome these issues by proposing a robust safe control framework for bounded state-dependent uncertainties. We first guarantee the feasibility of safe control for uncertain dynamics by learning a control-limits-aware, uncertainty-robust safety index. Then we show that robust safe control can be formulated as convex problems (Convex Semi-Infinite Programming or Second-Order Cone Programming) and propose corresponding optimal solvers that can run in real-time. In addition, we analyze when and how safety can be preserved under unmodeled uncertainties. Experiment results show that our method successfully finds robust safe control in real-time for different uncertainties and is much less conservative than a strong baseline algorithm.

A Contact-Safe Reinforcement Learning Framework for Contact-Rich Robot Manipulation

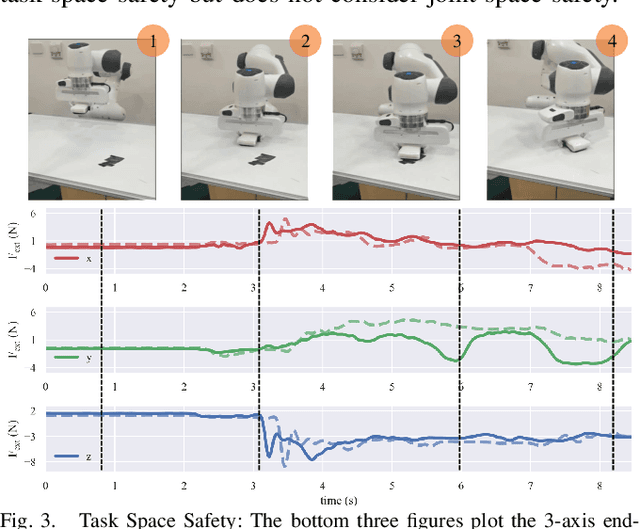
Reinforcement learning shows great potential to solve complex contact-rich robot manipulation tasks. However, the safety of using RL in the real world is a crucial problem, since unexpected dangerous collisions might happen when the RL policy is imperfect during training or in unseen scenarios. In this paper, we propose a contact-safe reinforcement learning framework for contact-rich robot manipulation, which maintains safety in both the task space and joint space. When the RL policy causes unexpected collisions between the robot arm and the environment, our framework is able to immediately detect the collision and ensure the contact force to be small. Furthermore, the end-effector is enforced to perform contact-rich tasks compliantly, while keeping robust to external disturbances. We train the RL policy in simulation and transfer it to the real robot. Real world experiments on robot wiping tasks show that our method is able to keep the contact force small both in task space and joint space even when the policy is under unseen scenario with unexpected collision, while rejecting the disturbances on the main task.