Robust Safe Control for Uncertain Dynamic Models
Paper and Code
Sep 14, 2022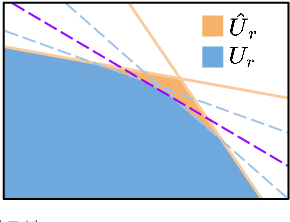
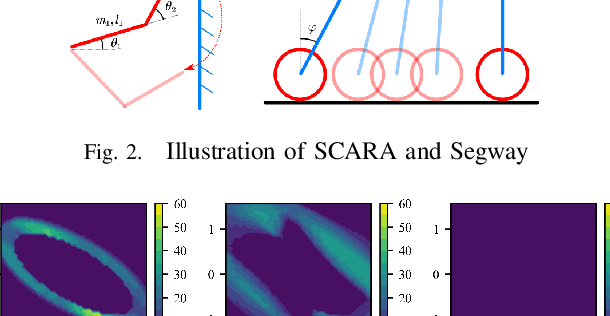
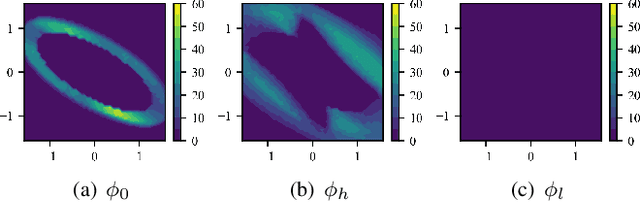
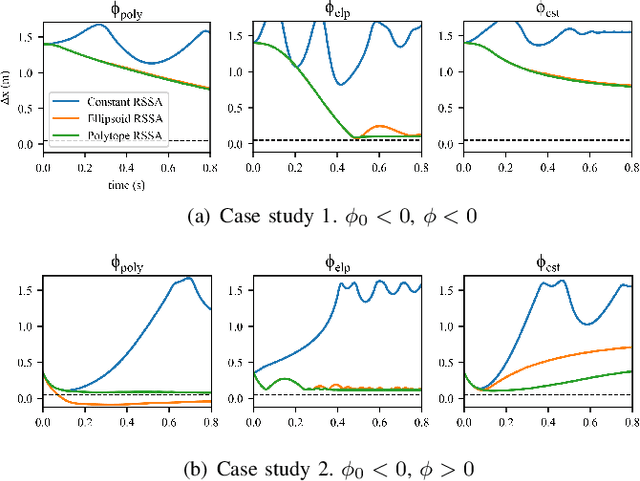
Model mismatches prevail in real-world applications. Hence it is important to design robust safe control algorithms for systems with uncertain dynamic models. The major challenge is that uncertainty results in difficulty in finding a feasible safe control in real-time. Existing methods usually simplify the problem such as restricting uncertainty type, ignoring control limits, or forgoing feasibility guarantees. In this work, we overcome these issues by proposing a robust safe control framework for bounded state-dependent uncertainties. We first guarantee the feasibility of safe control for uncertain dynamics by learning a control-limits-aware, uncertainty-robust safety index. Then we show that robust safe control can be formulated as convex problems (Convex Semi-Infinite Programming or Second-Order Cone Programming) and propose corresponding optimal solvers that can run in real-time. In addition, we analyze when and how safety can be preserved under unmodeled uncertainties. Experiment results show that our method successfully finds robust safe control in real-time for different uncertainties and is much less conservative than a strong baseline algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge