Shiyuan He
Pushing the Limits of Safety: A Technical Report on the ATLAS Challenge 2025
Jun 14, 2025Abstract:Multimodal Large Language Models (MLLMs) have enabled transformative advancements across diverse applications but remain susceptible to safety threats, especially jailbreak attacks that induce harmful outputs. To systematically evaluate and improve their safety, we organized the Adversarial Testing & Large-model Alignment Safety Grand Challenge (ATLAS) 2025}. This technical report presents findings from the competition, which involved 86 teams testing MLLM vulnerabilities via adversarial image-text attacks in two phases: white-box and black-box evaluations. The competition results highlight ongoing challenges in securing MLLMs and provide valuable guidance for developing stronger defense mechanisms. The challenge establishes new benchmarks for MLLM safety evaluation and lays groundwork for advancing safer multimodal AI systems. The code and data for this challenge are openly available at https://github.com/NY1024/ATLAS_Challenge_2025.
Functional Bayesian Additive Regression Trees with Shape Constraints
Feb 24, 2025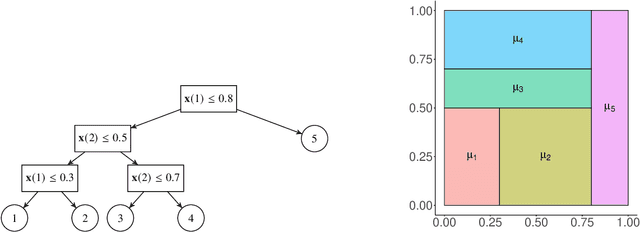
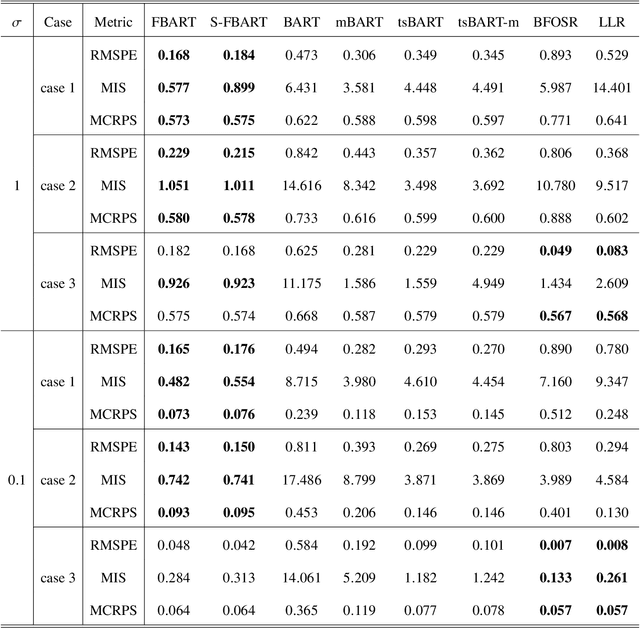
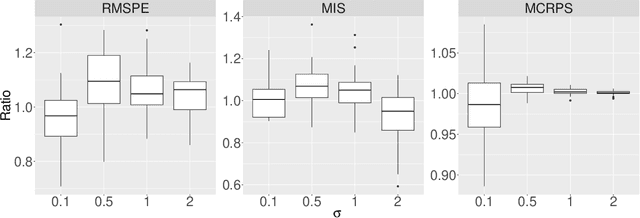
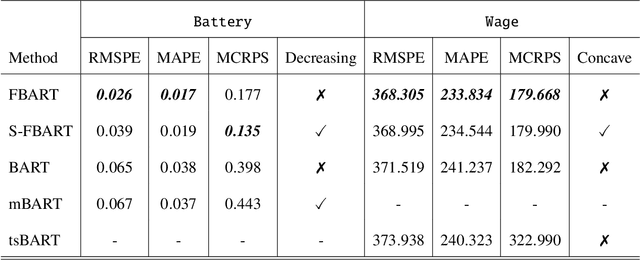
Abstract:Motivated by the great success of Bayesian additive regression trees (BART) on regression, we propose a nonparametric Bayesian approach for the function-on-scalar regression problem, termed as Functional BART (FBART). Utilizing spline-based function representation and tree-based domain partition model, FBART offers great flexibility in characterizing the complex and heterogeneous relationship between the response curve and scalar covariates. We devise a tailored Bayesian backfitting algorithm for estimating the parameters in the FBART model. Furthermore, we introduce an FBART model with shape constraints on the response curve, enhancing estimation and prediction performance when prior shape information of response curves is available. By incorporating a shape-constrained prior, we ensure that the posterior samples of the response curve satisfy the required shape constraints (e.g., monotonicity and/or convexity). Our proposed FBART model and its shape-constrained version are the new advances of BART models for functional data. Under certain regularity conditions, we derive the posterior convergence results for both FBART and its shape-constrained version. Finally, the superiority of the proposed methods over other competitive counterparts is validated through simulation experiments under various settings and analyses of two real datasets.
LoLDU: Low-Rank Adaptation via Lower-Diag-Upper Decomposition for Parameter-Efficient Fine-Tuning
Oct 17, 2024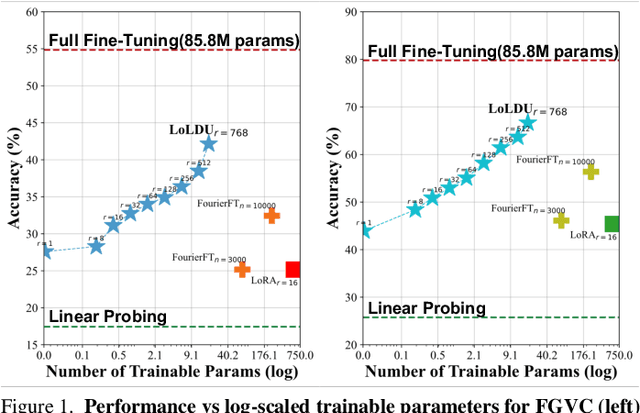
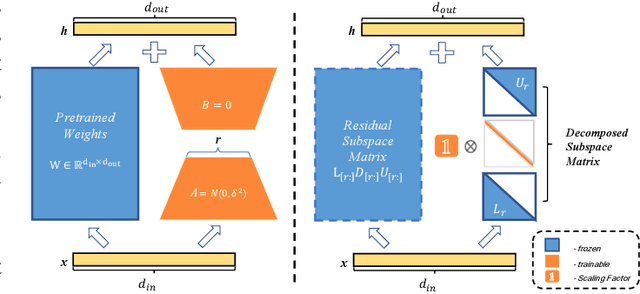
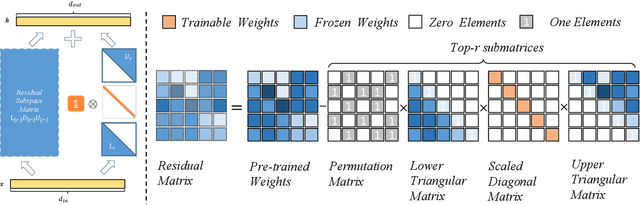
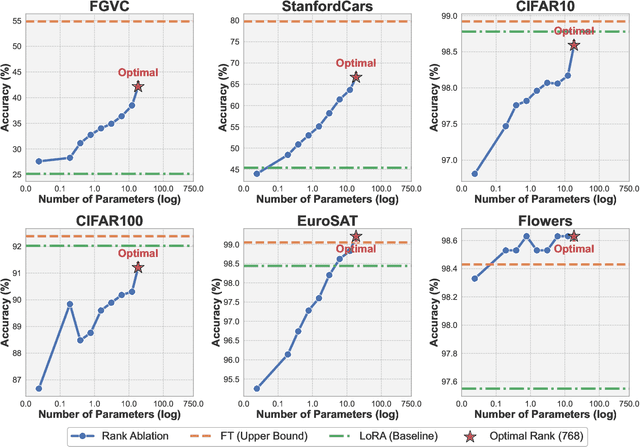
Abstract:The rapid growth of model scale has necessitated substantial computational resources for fine-tuning. Existing approach such as Low-Rank Adaptation (LoRA) has sought to address the problem of handling the large updated parameters in full fine-tuning. However, LoRA utilize random initialization and optimization of low-rank matrices to approximate updated weights, which can result in suboptimal convergence and an accuracy gap compared to full fine-tuning. To address these issues, we propose LoLDU, a Parameter-Efficient Fine-Tuning (PEFT) approach that significantly reduces trainable parameters by 2600 times compared to regular PEFT methods while maintaining comparable performance. LoLDU leverages Lower-Diag-Upper Decomposition (LDU) to initialize low-rank matrices for faster convergence and orthogonality. We focus on optimizing the diagonal matrix for scaling transformations. To the best of our knowledge, LoLDU has the fewest parameters among all PEFT approaches. We conducted extensive experiments across 4 instruction-following datasets, 6 natural language understanding (NLU) datasets, 8 image classification datasets, and image generation datasets with multiple model types (LLaMA2, RoBERTa, ViT, and Stable Diffusion), providing a comprehensive and detailed analysis. Our open-source code can be accessed at \href{https://github.com/SKDDJ/LoLDU}{https://github.com/SKDDJ/LoLDU}.
SVFit: Parameter-Efficient Fine-Tuning of Large Pre-Trained Models Using Singular Values
Sep 09, 2024

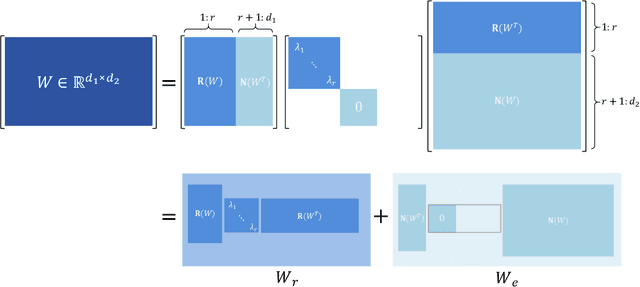

Abstract:Large pre-trained models (LPMs) have demonstrated exceptional performance in diverse natural language processing and computer vision tasks. However, fully fine-tuning these models poses substantial memory challenges, particularly in resource-constrained environments. Parameter-efficient fine-tuning (PEFT) methods, such as LoRA, mitigate this issue by adjusting only a small subset of parameters. Nevertheless, these methods typically employ random initialization for low-rank matrices, which can lead to inefficiencies in gradient descent and diminished generalizability due to suboptimal starting points. To address these limitations, we propose SVFit, a novel PEFT approach that leverages singular value decomposition (SVD) to initialize low-rank matrices using critical singular values as trainable parameters. Specifically, SVFit performs SVD on the pre-trained weight matrix to obtain the best rank-r approximation matrix, emphasizing the most critical singular values that capture over 99% of the matrix's information. These top-r singular values are then used as trainable parameters to scale the fundamental subspaces of the matrix, facilitating rapid domain adaptation. Extensive experiments across various pre-trained models in natural language understanding, text-to-image generation, and image classification tasks reveal that SVFit outperforms LoRA while requiring 16 times fewer trainable parameters.
A Unified Analysis of Multi-task Functional Linear Regression Models with Manifold Constraint and Composite Quadratic Penalty
Nov 09, 2022
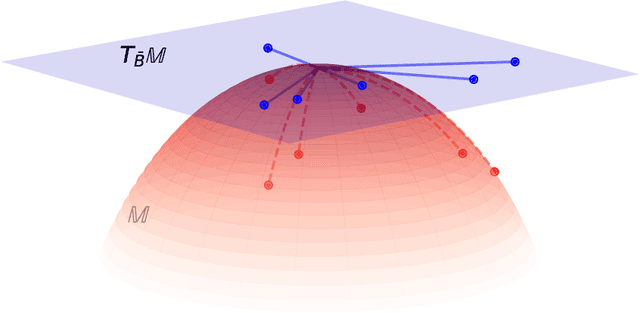

Abstract:This work studies the multi-task functional linear regression models where both the covariates and the unknown regression coefficients (called slope functions) are curves. For slope function estimation, we employ penalized splines to balance bias, variance, and computational complexity. The power of multi-task learning is brought in by imposing additional structures over the slope functions. We propose a general model with double regularization over the spline coefficient matrix: i) a matrix manifold constraint, and ii) a composite penalty as a summation of quadratic terms. Many multi-task learning approaches can be treated as special cases of this proposed model, such as a reduced-rank model and a graph Laplacian regularized model. We show the composite penalty induces a specific norm, which helps to quantify the manifold curvature and determine the corresponding proper subset in the manifold tangent space. The complexity of tangent space subset is then bridged to the complexity of geodesic neighbor via generic chaining. A unified convergence upper bound is obtained and specifically applied to the reduced-rank model and the graph Laplacian regularized model. The phase transition behaviors for the estimators are examined as we vary the configurations of model parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge