A Unified Analysis of Multi-task Functional Linear Regression Models with Manifold Constraint and Composite Quadratic Penalty

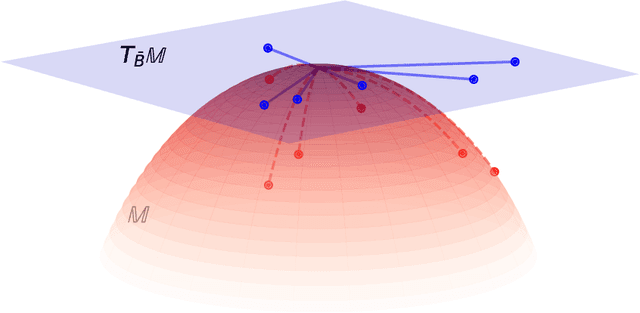
This work studies the multi-task functional linear regression models where both the covariates and the unknown regression coefficients (called slope functions) are curves. For slope function estimation, we employ penalized splines to balance bias, variance, and computational complexity. The power of multi-task learning is brought in by imposing additional structures over the slope functions. We propose a general model with double regularization over the spline coefficient matrix: i) a matrix manifold constraint, and ii) a composite penalty as a summation of quadratic terms. Many multi-task learning approaches can be treated as special cases of this proposed model, such as a reduced-rank model and a graph Laplacian regularized model. We show the composite penalty induces a specific norm, which helps to quantify the manifold curvature and determine the corresponding proper subset in the manifold tangent space. The complexity of tangent space subset is then bridged to the complexity of geodesic neighbor via generic chaining. A unified convergence upper bound is obtained and specifically applied to the reduced-rank model and the graph Laplacian regularized model. The phase transition behaviors for the estimators are examined as we vary the configurations of model parameters.

CP Degeneracy in Tensor Regression

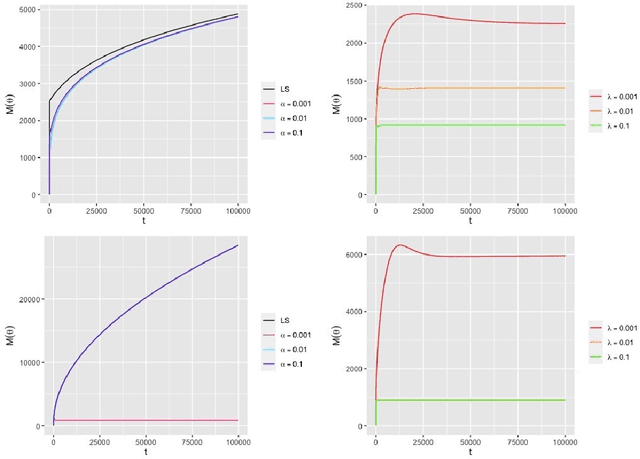
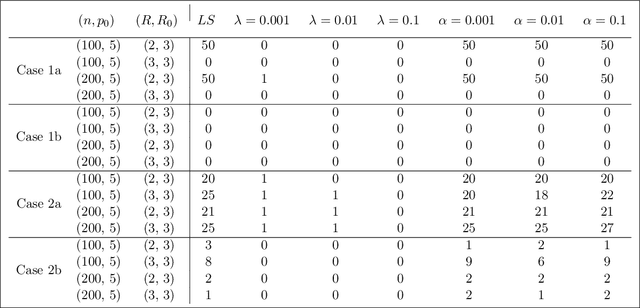
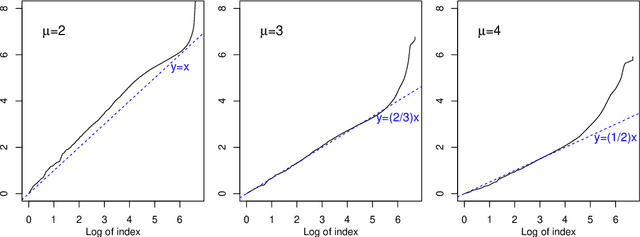
Tensor linear regression is an important and useful tool for analyzing tensor data. To deal with high dimensionality, CANDECOMP/PARAFAC (CP) low-rank constraints are often imposed on the coefficient tensor parameter in the (penalized) $M$-estimation. However, we show that the corresponding optimization may not be attainable, and when this happens, the estimator is not well-defined. This is closely related to a phenomenon, called CP degeneracy, in low-rank tensor approximation problems. In this article, we provide useful results of CP degeneracy in tensor regression problems. In addition, we provide a general penalized strategy as a solution to overcome CP degeneracy. The asymptotic properties of the resulting estimation are also studied. Numerical experiments are conducted to illustrate our findings.