Personalized Coupled Tensor Decomposition for Multimodal Data Fusion: Uniqueness and Algorithms

Coupled tensor decompositions (CTDs) perform data fusion by linking factors from different datasets. Although many CTDs have been already proposed, current works do not address important challenges of data fusion, where: 1) the datasets are often heterogeneous, constituting different "views" of a given phenomena (multimodality); and 2) each dataset can contain personalized or dataset-specific information, constituting distinct factors that are not coupled with other datasets. In this work, we introduce a personalized CTD framework tackling these challenges. A flexible model is proposed where each dataset is represented as the sum of two components, one related to a common tensor through a multilinear measurement model, and another specific to each dataset. Both the common and distinct components are assumed to admit a polyadic decomposition. This generalizes several existing CTD models. We provide conditions for specific and generic uniqueness of the decomposition that are easy to interpret. These conditions employ uni-mode uniqueness of different individual datasets and properties of the measurement model. Two algorithms are proposed to compute the common and distinct components: a semi-algebraic one and a coordinate-descent optimization method. Experimental results illustrate the advantage of the proposed framework compared with the state of the art approaches.

Hierarchical Homogeneity-Based Superpixel Segmentation: Application to Hyperspectral Image Analysis

Hyperspectral image (HI) analysis approaches have recently become increasingly complex and sophisticated. Recently, the combination of spectral-spatial information and superpixel techniques have addressed some hyperspectral data issues, such as the higher spatial variability of spectral signatures and dimensionality of the data. However, most existing superpixel approaches do not account for specific HI characteristics resulting from its high spectral dimension. In this work, we propose a multiscale superpixel method that is computationally efficient for processing hyperspectral data. The Simple Linear Iterative Clustering (SLIC) oversegmentation algorithm, on which the technique is based, has been extended hierarchically. Using a novel robust homogeneity testing, the proposed hierarchical approach leads to superpixels of variable sizes but with higher spectral homogeneity when compared to the classical SLIC segmentation. For validation, the proposed homogeneity-based hierarchical method was applied as a preprocessing step in the spectral unmixing and classification tasks carried out using, respectively, the Multiscale sparse Unmixing Algorithm (MUA) and the CNN-Enhanced Graph Convolutional Network (CEGCN) methods. Simulation results with both synthetic and real data show that the technique is competitive with state-of-the-art solutions.

Learning Semilinear Neural Operators : A Unified Recursive Framework For Prediction And Data Assimilation

Recent advances in the theory of Neural Operators (NOs) have enabled fast and accurate computation of the solutions to complex systems described by partial differential equations (PDEs). Despite their great success, current NO-based solutions face important challenges when dealing with spatio-temporal PDEs over long time scales. Specifically, the current theory of NOs does not present a systematic framework to perform data assimilation and efficiently correct the evolution of PDE solutions over time based on sparsely sampled noisy measurements. In this paper, we propose a learning-based state-space approach to compute the solution operators to infinite-dimensional semilinear PDEs. Exploiting the structure of semilinear PDEs and the theory of nonlinear observers in function spaces, we develop a flexible recursive method that allows for both prediction and data assimilation by combining prediction and correction operations. The proposed framework is capable of producing fast and accurate predictions over long time horizons, dealing with irregularly sampled noisy measurements to correct the solution, and benefits from the decoupling between the spatial and temporal dynamics of this class of PDEs. We show through experiments on the Kuramoto-Sivashinsky, Navier-Stokes and Korteweg-de Vries equations that the proposed model is robust to noise and can leverage arbitrary amounts of measurements to correct its prediction over a long time horizon with little computational overhead.

A Generalized Multiscale Bundle-Based Hyperspectral Sparse Unmixing Algorithm

In hyperspectral sparse unmixing, a successful approach employs spectral bundles to address the variability of the endmembers in the spatial domain. However, the regularization penalties usually employed aggregate substantial computational complexity, and the solutions are very noise-sensitive. We generalize a multiscale spatial regularization approach to solve the unmixing problem by incorporating group sparsity-inducing mixed norms. Then, we propose a noise-robust method that can take advantage of the bundle structure to deal with endmember variability while ensuring inter- and intra-class sparsity in abundance estimation with reasonable computational cost. We also present a general heuristic to select the \emph{most representative} abundance estimation over multiple runs of the unmixing process, yielding a solution that is robust and highly reproducible. Experiments illustrate the robustness and consistency of the results when compared to related methods.

On the Impact of Sampling on Deep Sequential State Estimation

State inference and parameter learning in sequential models can be successfully performed with approximation techniques that maximize the evidence lower bound to the marginal log-likelihood of the data distribution. These methods may be referred to as Dynamical Variational Autoencoders, and our specific focus lies on the deep Kalman filter. It has been shown that the ELBO objective can oversimplify data representations, potentially compromising estimation quality. Tighter Monte Carlo objectives have been proposed in the literature to enhance generative modeling performance. For instance, the IWAE objective uses importance weights to reduce the variance of marginal log-likelihood estimates. In this paper, importance sampling is applied to the DKF framework for learning deep Markov models, resulting in the IW-DKF, which shows an improvement in terms of log-likelihood estimates and KL divergence between the variational distribution and the transition model. The framework using the sampled DKF update rule is also accommodated to address sequential state and parameter estimation when working with highly non-linear physics-based models. An experiment with the 3-space Lorenz attractor shows an enhanced generative modeling performance and also a decrease in RMSE when estimating the model parameters and latent states, indicating that tighter MCOs lead to improved state inference performance.

Learning Interpretable Deep Disentangled Neural Networks for Hyperspectral Unmixing

Although considerable effort has been dedicated to improving the solution to the hyperspectral unmixing problem, non-idealities such as complex radiation scattering and endmember variability negatively impact the performance of most existing algorithms and can be very challenging to address. Recently, deep learning-based frameworks have been explored for hyperspectral umixing due to their flexibility and powerful representation capabilities. However, such techniques either do not address the non-idealities of the unmixing problem, or rely on black-box models which are not interpretable. In this paper, we propose a new interpretable deep learning method for hyperspectral unmixing that accounts for nonlinearity and endmember variability. The proposed method leverages a probabilistic variational deep-learning framework, where disentanglement learning is employed to properly separate the abundances and endmembers. The model is learned end-to-end using stochastic backpropagation, and trained using a self-supervised strategy which leverages benefits from semi-supervised learning techniques. Furthermore, the model is carefully designed to provide a high degree of interpretability. This includes modeling the abundances as a Dirichlet distribution, the endmembers using low-dimensional deep latent variable representations, and using two-stream neural networks composed of additive piecewise-linear/nonlinear components. Experimental results on synthetic and real datasets illustrate the performance of the proposed method compared to state-of-the-art algorithms.

Dynamical Hyperspectral Unmixing with Variational Recurrent Neural Networks

Multitemporal hyperspectral unmixing (MTHU) is a fundamental tool in the analysis of hyperspectral image sequences. It reveals the dynamical evolution of the materials (endmembers) and of their proportions (abundances) in a given scene. However, adequately accounting for the spatial and temporal variability of the endmembers in MTHU is challenging, and has not been fully addressed so far in unsupervised frameworks. In this work, we propose an unsupervised MTHU algorithm based on variational recurrent neural networks. First, a stochastic model is proposed to represent both the dynamical evolution of the endmembers and their abundances, as well as the mixing process. Moreover, a new model based on a low-dimensional parametrization is used to represent spatial and temporal endmember variability, significantly reducing the amount of variables to be estimated. We propose to formulate MTHU as a Bayesian inference problem. However, the solution to this problem does not have an analytical solution due to the nonlinearity and non-Gaussianity of the model. Thus, we propose a solution based on deep variational inference, in which the posterior distribution of the estimated abundances and endmembers is represented by using a combination of recurrent neural networks and a physically motivated model. The parameters of the model are learned using stochastic backpropagation. Experimental results show that the proposed method outperforms state of the art MTHU algorithms.

Coupled CP tensor decomposition with shared and distinct components for multi-task fMRI data fusion

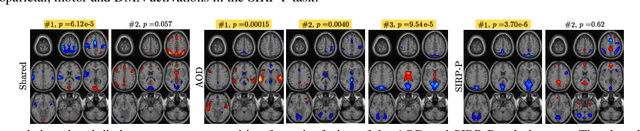
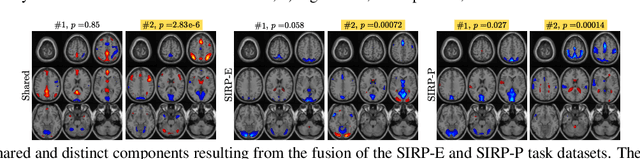
Discovering components that are shared in multiple datasets, next to dataset-specific features, has great potential for studying the relationships between different subjects or tasks in functional Magnetic Resonance Imaging (fMRI) data. Coupled matrix and tensor factorization approaches have been useful for flexible data fusion, or decomposition to extract features that can be used in multiple ways. However, existing methods do not directly recover shared and dataset-specific components, which requires post-processing steps involving additional hyperparameter selection. In this paper, we propose a tensor-based framework for multi-task fMRI data fusion, using a partially constrained canonical polyadic (CP) decomposition model. Differently from previous approaches, the proposed method directly recovers shared and dataset-specific components, leading to results that are directly interpretable. A strategy to select a highly reproducible solution to the decomposition is also proposed. We evaluate the proposed methodology on real fMRI data of three tasks, and show that the proposed method finds meaningful components that clearly identify group differences between patients with schizophrenia and healthy controls.

Deep Hyperspectral and Multispectral Image Fusion with Inter-image Variability

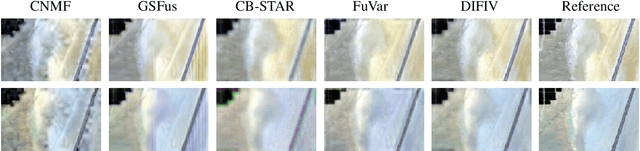
Hyperspectral and multispectral image fusion allows us to overcome the hardware limitations of hyperspectral imaging systems inherent to their lower spatial resolution. Nevertheless, existing algorithms usually fail to consider realistic image acquisition conditions. This paper presents a general imaging model that considers inter-image variability of data from heterogeneous sources and flexible image priors. The fusion problem is stated as an optimization problem in the maximum a posteriori framework. We introduce an original image fusion method that, on the one hand, solves the optimization problem accounting for inter-image variability with an iteratively reweighted scheme and, on the other hand, that leverages light-weight CNN-based networks to learn realistic image priors from data. In addition, we propose a zero-shot strategy to directly learn the image-specific prior of the latent images in an unsupervised manner. The performance of the algorithm is illustrated with real data subject to inter-image variability.

Model-Based Deep Autoencoder Networks for Nonlinear Hyperspectral Unmixing

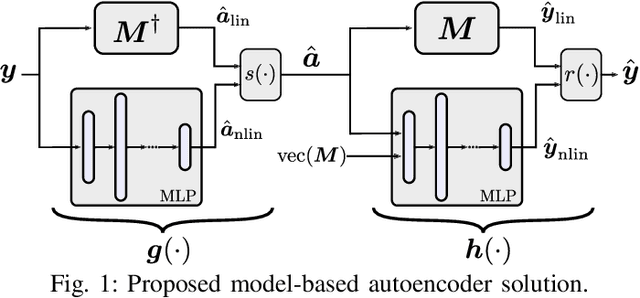
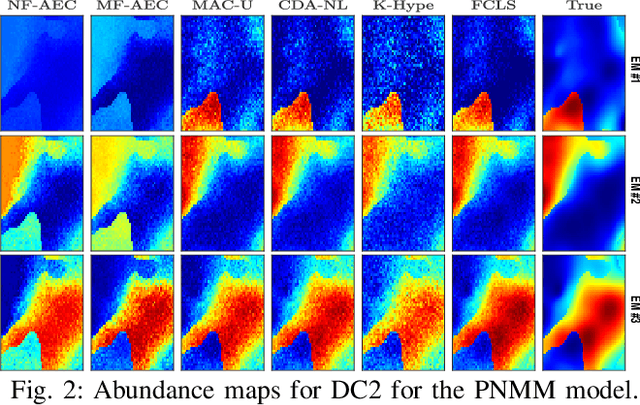
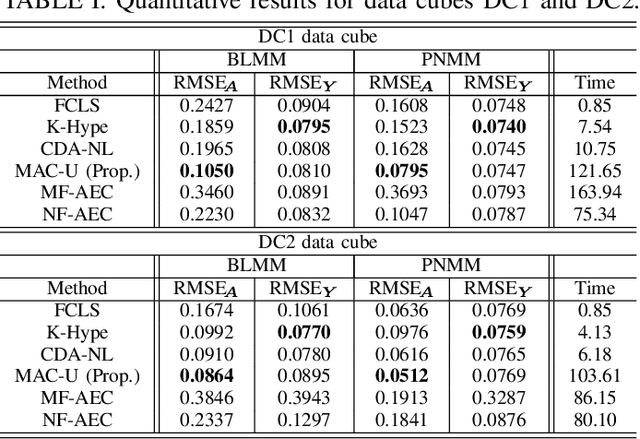
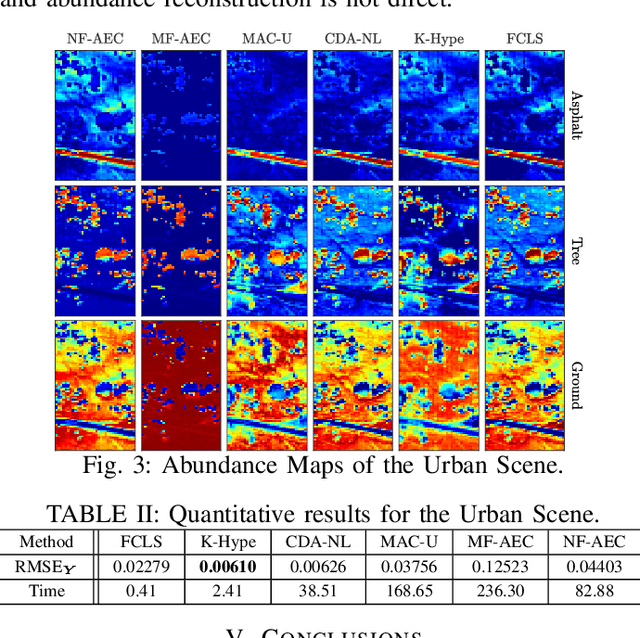
Autoencoder (AEC) networks have recently emerged as a promising approach to perform unsupervised hyperspectral unmixing (HU) by associating the latent representations with the abundances, the decoder with the mixing model and the encoder with its inverse. AECs are especially appealing for nonlinear HU since they lead to unsupervised and model-free algorithms. However, existing approaches fail to explore the fact that the encoder should invert the mixing process, which might reduce their robustness. In this paper, we propose a model-based AEC for nonlinear HU by considering the mixing model a nonlinear fluctuation over a linear mixture. Differently from previous works, we show that this restriction naturally imposes a particular structure to both the encoder and to the decoder networks. This introduces prior information in the AEC without reducing the flexibility of the mixing model. Simulations with synthetic and real data indicate that the proposed strategy improves nonlinear HU.