Personalized Coupled Tensor Decomposition for Multimodal Data Fusion: Uniqueness and Algorithms

Coupled tensor decompositions (CTDs) perform data fusion by linking factors from different datasets. Although many CTDs have been already proposed, current works do not address important challenges of data fusion, where: 1) the datasets are often heterogeneous, constituting different "views" of a given phenomena (multimodality); and 2) each dataset can contain personalized or dataset-specific information, constituting distinct factors that are not coupled with other datasets. In this work, we introduce a personalized CTD framework tackling these challenges. A flexible model is proposed where each dataset is represented as the sum of two components, one related to a common tensor through a multilinear measurement model, and another specific to each dataset. Both the common and distinct components are assumed to admit a polyadic decomposition. This generalizes several existing CTD models. We provide conditions for specific and generic uniqueness of the decomposition that are easy to interpret. These conditions employ uni-mode uniqueness of different individual datasets and properties of the measurement model. Two algorithms are proposed to compute the common and distinct components: a semi-algebraic one and a coordinate-descent optimization method. Experimental results illustrate the advantage of the proposed framework compared with the state of the art approaches.

Coupled CP tensor decomposition with shared and distinct components for multi-task fMRI data fusion

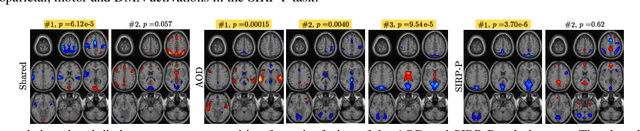
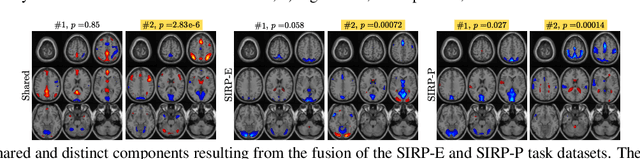
Discovering components that are shared in multiple datasets, next to dataset-specific features, has great potential for studying the relationships between different subjects or tasks in functional Magnetic Resonance Imaging (fMRI) data. Coupled matrix and tensor factorization approaches have been useful for flexible data fusion, or decomposition to extract features that can be used in multiple ways. However, existing methods do not directly recover shared and dataset-specific components, which requires post-processing steps involving additional hyperparameter selection. In this paper, we propose a tensor-based framework for multi-task fMRI data fusion, using a partially constrained canonical polyadic (CP) decomposition model. Differently from previous approaches, the proposed method directly recovers shared and dataset-specific components, leading to results that are directly interpretable. A strategy to select a highly reproducible solution to the decomposition is also proposed. We evaluate the proposed methodology on real fMRI data of three tasks, and show that the proposed method finds meaningful components that clearly identify group differences between patients with schizophrenia and healthy controls.