HP-BERT: A framework for longitudinal study of Hinduphobia on social media via LLMs

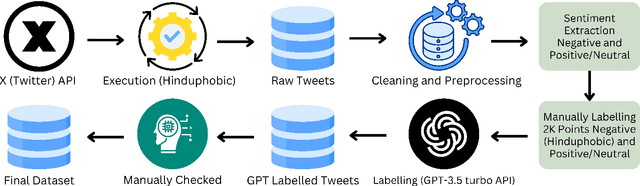
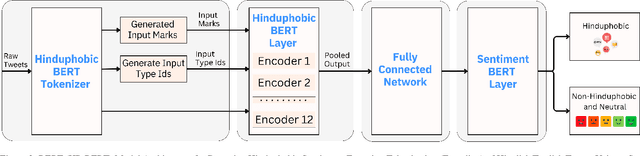
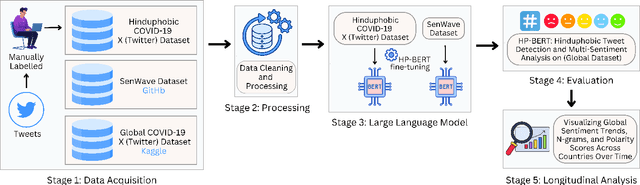
During the COVID-19 pandemic, community tensions intensified, fuelling Hinduphobic sentiments and discrimination against individuals of Hindu descent within India and worldwide. Large language models (LLMs) have become prominent in natural language processing (NLP) tasks and social media analysis, enabling longitudinal studies of platforms like X (formerly Twitter) for specific issues during COVID-19. We present an abuse detection and sentiment analysis framework that offers a longitudinal analysis of Hinduphobia on X (Twitter) during and after the COVID-19 pandemic. This framework assesses the prevalence and intensity of Hinduphobic discourse, capturing elements such as derogatory jokes and racist remarks through sentiment analysis and abuse detection from pre-trained and fine-tuned LLMs. Additionally, we curate and publish a "Hinduphobic COVID-19 X (Twitter) Dataset" of 8,000 tweets annotated for Hinduphobic abuse detection, which is used to fine-tune a BERT model, resulting in the development of the Hinduphobic BERT (HP-BERT) model. We then further fine-tune HP-BERT using the SenWave dataset for multi-label sentiment analysis. Our study encompasses approximately 27.4 million tweets from six countries, including Australia, Brazil, India, Indonesia, Japan, and the United Kingdom. Our findings reveal a strong correlation between spikes in COVID-19 cases and surges in Hinduphobic rhetoric, highlighting how political narratives, misinformation, and targeted jokes contributed to communal polarisation. These insights provide valuable guidance for developing strategies to mitigate communal tensions in future crises, both locally and globally. We advocate implementing automated monitoring and removal of such content on social media to curb divisive discourse.

Machine Learning Algorithms for Detecting Mental Stress in College Students

In today's world, stress is a big problem that affects people's health and happiness. More and more people are feeling stressed out, which can lead to lots of health issues like breathing problems, feeling overwhelmed, heart attack, diabetes, etc. This work endeavors to forecast stress and non-stress occurrences among college students by applying various machine learning algorithms: Decision Trees, Random Forest, Support Vector Machines, AdaBoost, Naive Bayes, Logistic Regression, and K-nearest Neighbors. The primary objective of this work is to leverage a research study to predict and mitigate stress and non-stress based on the collected questionnaire dataset. We conducted a workshop with the primary goal of studying the stress levels found among the students. This workshop was attended by Approximately 843 students aged between 18 to 21 years old. A questionnaire was given to the students validated under the guidance of the experts from the All India Institute of Medical Sciences (AIIMS) Raipur, Chhattisgarh, India, on which our dataset is based. The survey consists of 28 questions, aiming to comprehensively understand the multidimensional aspects of stress, including emotional well-being, physical health, academic performance, relationships, and leisure. This work finds that Support Vector Machines have a maximum accuracy for Stress, reaching 95\%. The study contributes to a deeper understanding of stress determinants. It aims to improve college student's overall quality of life and academic success, addressing the multifaceted nature of stress.

KODA: A Data-Driven Recursive Model for Time Series Forecasting and Data Assimilation using Koopman Operators

Approaches based on Koopman operators have shown great promise in forecasting time series data generated by complex nonlinear dynamical systems (NLDS). Although such approaches are able to capture the latent state representation of a NLDS, they still face difficulty in long term forecasting when applied to real world data. Specifically many real-world NLDS exhibit time-varying behavior, leading to nonstationarity that is hard to capture with such models. Furthermore they lack a systematic data-driven approach to perform data assimilation, that is, exploiting noisy measurements on the fly in the forecasting task. To alleviate the above issues, we propose a Koopman operator-based approach (named KODA - Koopman Operator with Data Assimilation) that integrates forecasting and data assimilation in NLDS. In particular we use a Fourier domain filter to disentangle the data into a physical component whose dynamics can be accurately represented by a Koopman operator, and residual dynamics that represents the local or time varying behavior that are captured by a flexible and learnable recursive model. We carefully design an architecture and training criterion that ensures this decomposition lead to stable and long-term forecasts. Moreover, we introduce a course correction strategy to perform data assimilation with new measurements at inference time. The proposed approach is completely data-driven and can be learned end-to-end. Through extensive experimental comparisons we show that KODA outperforms existing state of the art methods on multiple time series benchmarks such as electricity, temperature, weather, lorenz 63 and duffing oscillator demonstrating its superior performance and efficacy along the three tasks a) forecasting, b) data assimilation and c) state prediction.

Learning Semilinear Neural Operators : A Unified Recursive Framework For Prediction And Data Assimilation

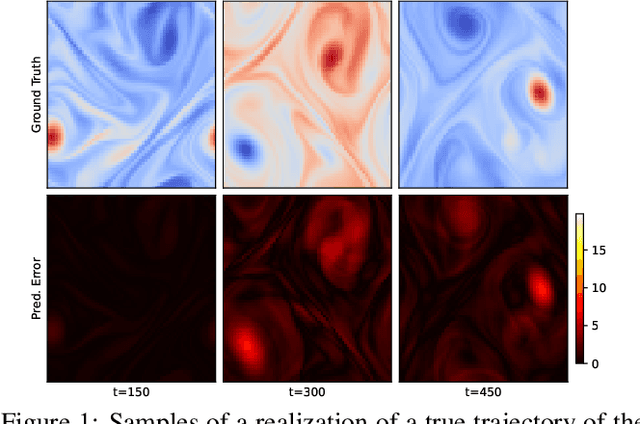
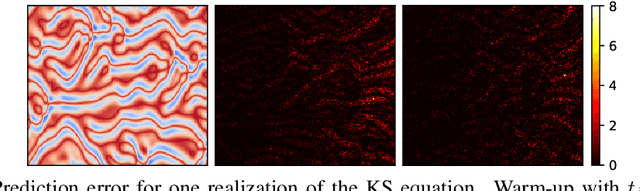
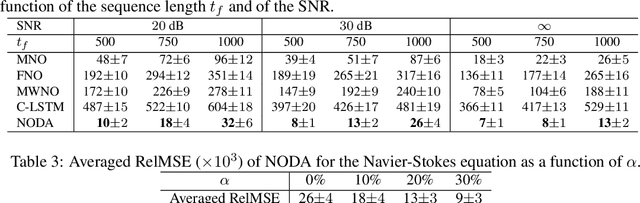
Recent advances in the theory of Neural Operators (NOs) have enabled fast and accurate computation of the solutions to complex systems described by partial differential equations (PDEs). Despite their great success, current NO-based solutions face important challenges when dealing with spatio-temporal PDEs over long time scales. Specifically, the current theory of NOs does not present a systematic framework to perform data assimilation and efficiently correct the evolution of PDE solutions over time based on sparsely sampled noisy measurements. In this paper, we propose a learning-based state-space approach to compute the solution operators to infinite-dimensional semilinear PDEs. Exploiting the structure of semilinear PDEs and the theory of nonlinear observers in function spaces, we develop a flexible recursive method that allows for both prediction and data assimilation by combining prediction and correction operations. The proposed framework is capable of producing fast and accurate predictions over long time horizons, dealing with irregularly sampled noisy measurements to correct the solution, and benefits from the decoupling between the spatial and temporal dynamics of this class of PDEs. We show through experiments on the Kuramoto-Sivashinsky, Navier-Stokes and Korteweg-de Vries equations that the proposed model is robust to noise and can leverage arbitrary amounts of measurements to correct its prediction over a long time horizon with little computational overhead.

Inv-SENnet: Invariant Self Expression Network for clustering under biased data

Subspace clustering algorithms are used for understanding the cluster structure that explains the dataset well. These methods are extensively used for data-exploration tasks in various areas of Natural Sciences. However, most of these methods fail to handle unwanted biases in datasets. For datasets where a data sample represents multiple attributes, naively applying any clustering approach can result in undesired output. To this end, we propose a novel framework for jointly removing unwanted attributes (biases) while learning to cluster data points in individual subspaces. Assuming we have information about the bias, we regularize the clustering method by adversarially learning to minimize the mutual information between the data and the unwanted attributes. Our experimental result on synthetic and real-world datasets demonstrate the effectiveness of our approach.

Variation is the Norm: Brain State Dynamics Evoked By Emotional Video Clips

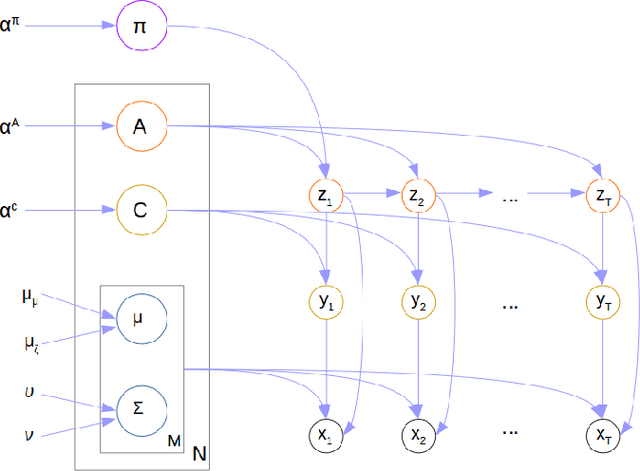
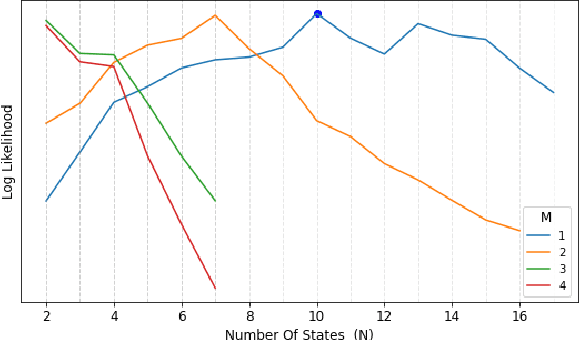
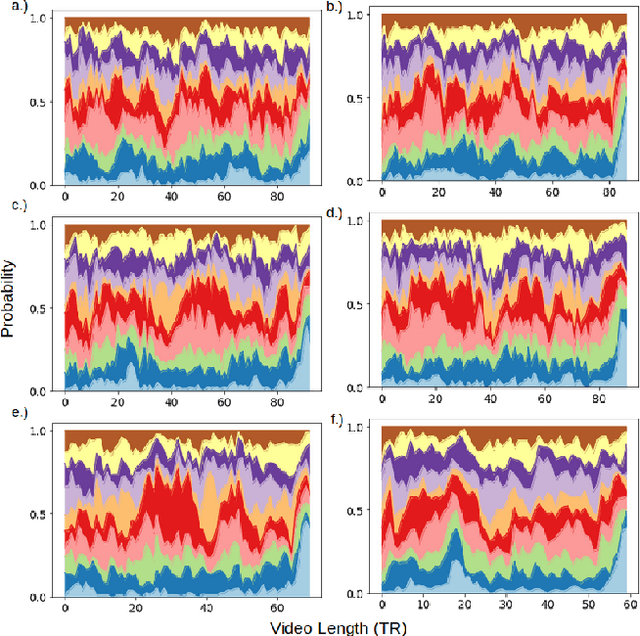
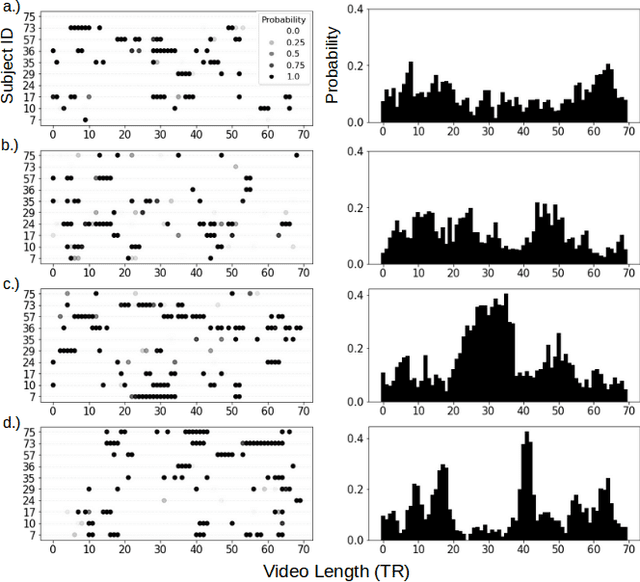
For the last several decades, emotion research has attempted to identify a "biomarker" or consistent pattern of brain activity to characterize a single category of emotion (e.g., fear) that will remain consistent across all instances of that category, regardless of individual and context. In this study, we investigated variation rather than consistency during emotional experiences while people watched video clips chosen to evoke instances of specific emotion categories. Specifically, we developed a sequential probabilistic approach to model the temporal dynamics in a participant's brain activity during video viewing. We characterized brain states during these clips as distinct state occupancy periods between state transitions in blood oxygen level dependent (BOLD) signal patterns. We found substantial variation in the state occupancy probability distributions across individuals watching the same video, supporting the hypothesis that when it comes to the brain correlates of emotional experience, variation may indeed be the norm.

A Distributed Model-Free Algorithm for Multi-hop Ride-sharing using Deep Reinforcement Learning

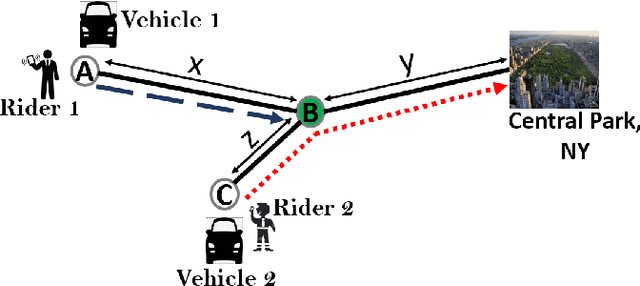
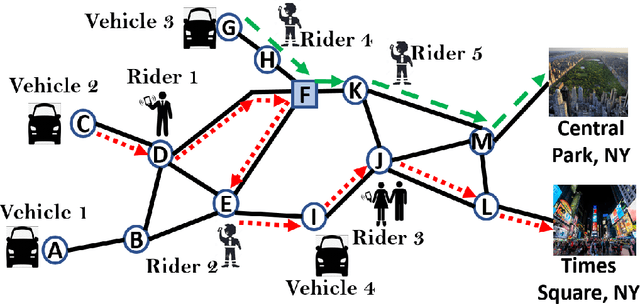
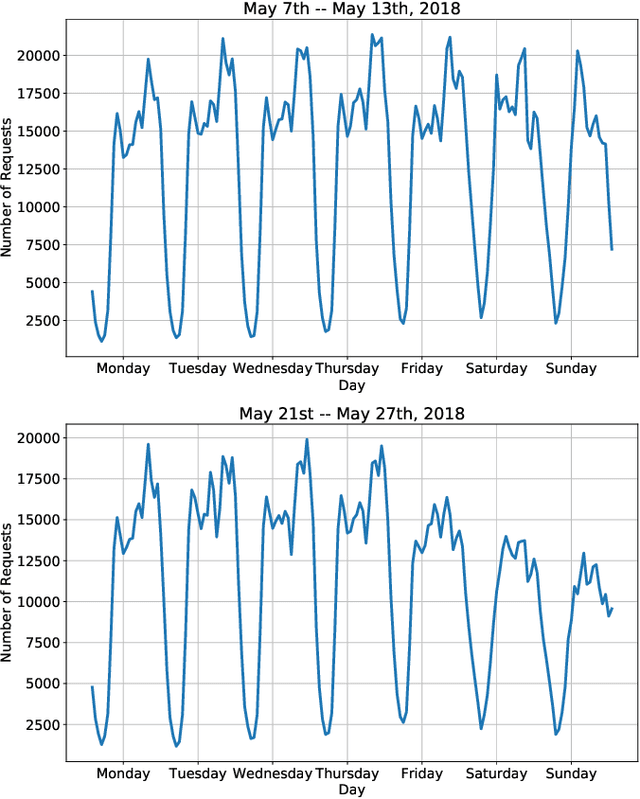
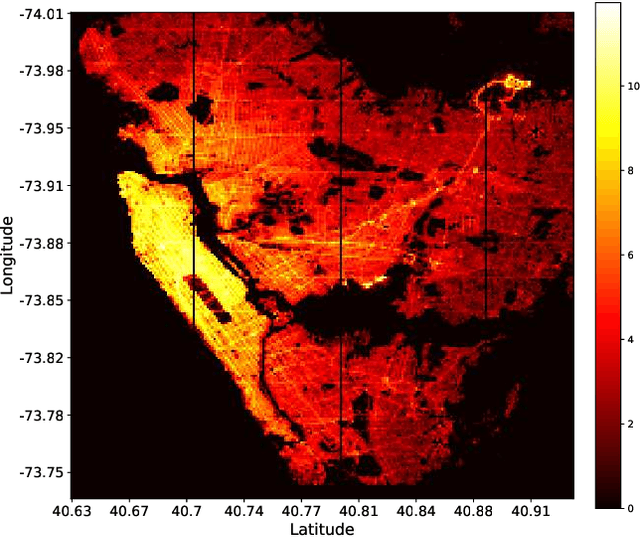
The growth of autonomous vehicles, ridesharing systems, and self driving technology will bring a shift in the way ride hailing platforms plan out their services. However, these advances in technology coupled with road congestion, environmental concerns, fuel usage, vehicles emissions, and the high cost of the vehicle usage have brought more attention to better utilize the use of vehicles and their capacities. In this paper, we propose a novel multi-hop ride-sharing (MHRS) algorithm that uses deep reinforcement learning to learn optimal vehicle dispatch and matching decisions by interacting with the external environment. By allowing customers to transfer between vehicles, i.e., ride with one vehicle for sometime and then transfer to another one, MHRS helps in attaining 30\% lower cost and 20\% more efficient utilization of fleets, as compared to the ride-sharing algorithms. This flexibility of multi-hop feature gives a seamless experience to customers and ride-sharing companies, and thus improves ride-sharing services.