A Distributed Model-Free Algorithm for Multi-hop Ride-sharing using Deep Reinforcement Learning

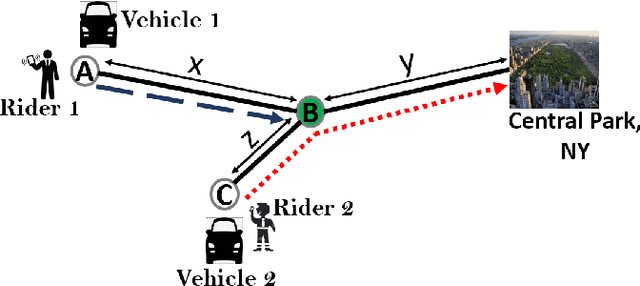
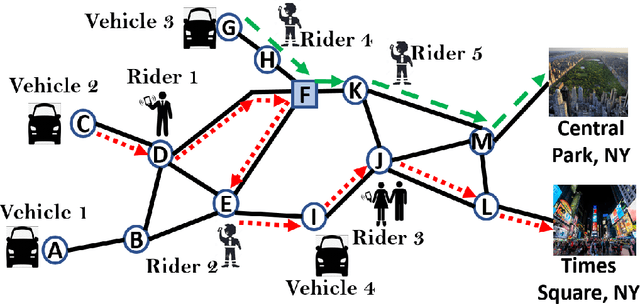
The growth of autonomous vehicles, ridesharing systems, and self driving technology will bring a shift in the way ride hailing platforms plan out their services. However, these advances in technology coupled with road congestion, environmental concerns, fuel usage, vehicles emissions, and the high cost of the vehicle usage have brought more attention to better utilize the use of vehicles and their capacities. In this paper, we propose a novel multi-hop ride-sharing (MHRS) algorithm that uses deep reinforcement learning to learn optimal vehicle dispatch and matching decisions by interacting with the external environment. By allowing customers to transfer between vehicles, i.e., ride with one vehicle for sometime and then transfer to another one, MHRS helps in attaining 30\% lower cost and 20\% more efficient utilization of fleets, as compared to the ride-sharing algorithms. This flexibility of multi-hop feature gives a seamless experience to customers and ride-sharing companies, and thus improves ride-sharing services.

DeepPool: Distributed Model-free Algorithm for Ride-sharing using Deep Reinforcement Learning

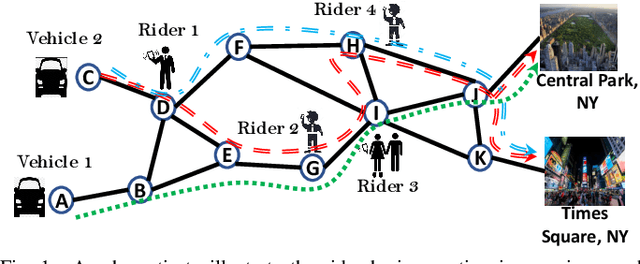
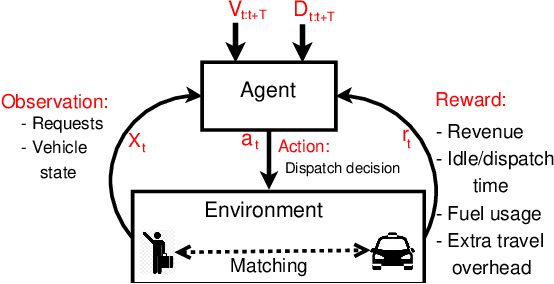
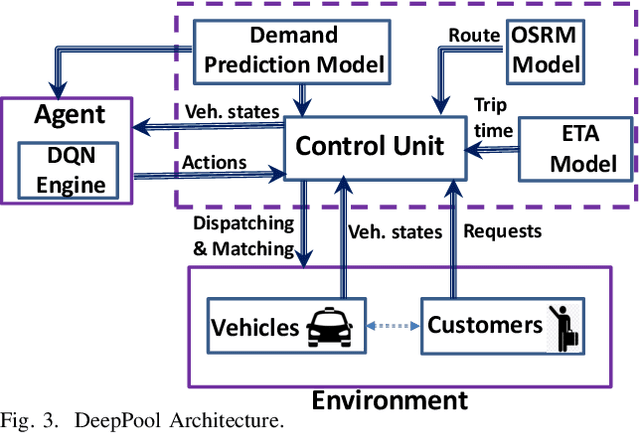
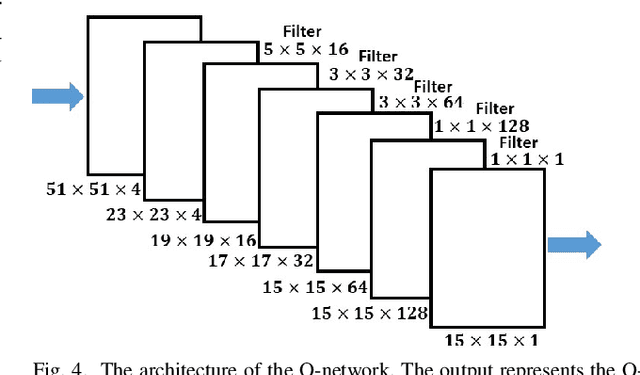
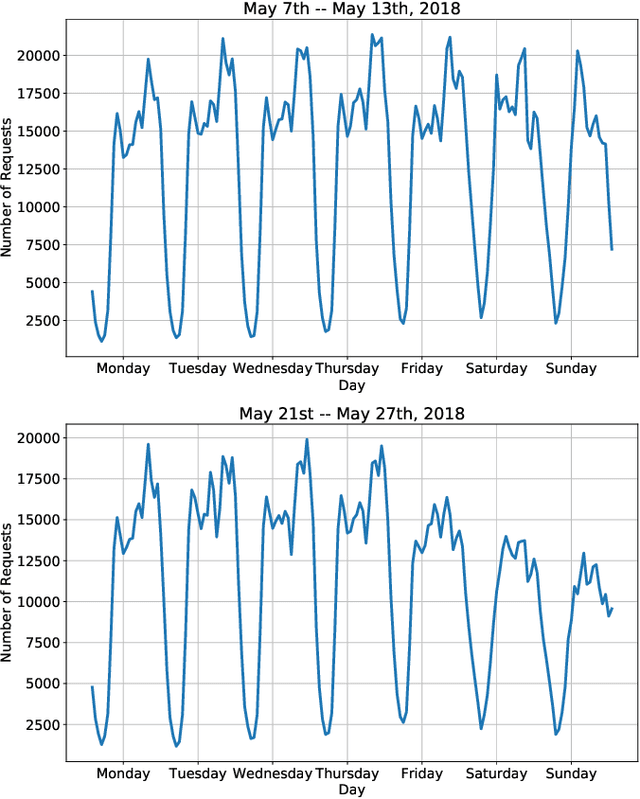
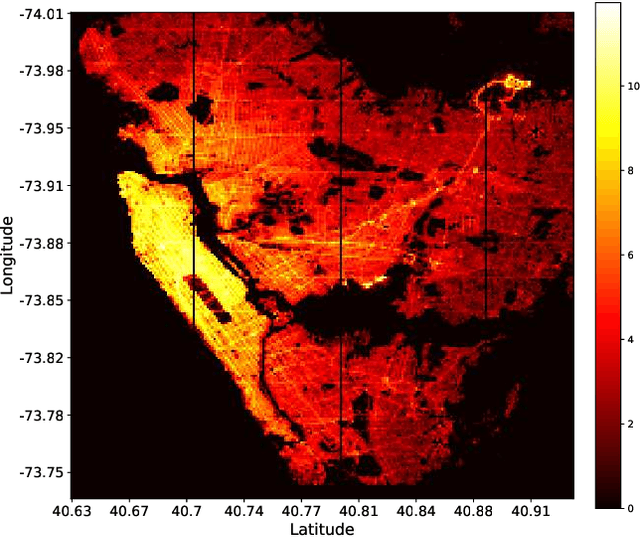
The success of modern ride-sharing platforms crucially depends on the profit of the ride-sharing fleet operating companies, and how efficiently the resources are managed. Further, ride-sharing allows sharing costs and, hence, reduces the congestion and emission by making better use of vehicle capacities. In this work, we develop a distributed model-free, DeepPool, that uses deep Q-network (DQN) techniques to learn optimal dispatch policies by interacting with the environment. Further, DeepPool efficiently incorporates travel demand statistics and deep learning models to manage dispatching vehicles for improved ride sharing services. Using real-world dataset of taxi trip records in New York City, DeepPool performs better than other strategies, proposed in the literature, that do not consider ride sharing or do not dispatch the vehicles to regions where the future demand is anticipated. Finally, DeepPool can adapt rapidly to dynamic environments since it is implemented in a distributed manner in which each vehicle solves its own DQN individually without coordination.