On the Impact of Sampling on Deep Sequential State Estimation
Paper and Code
Nov 28, 2023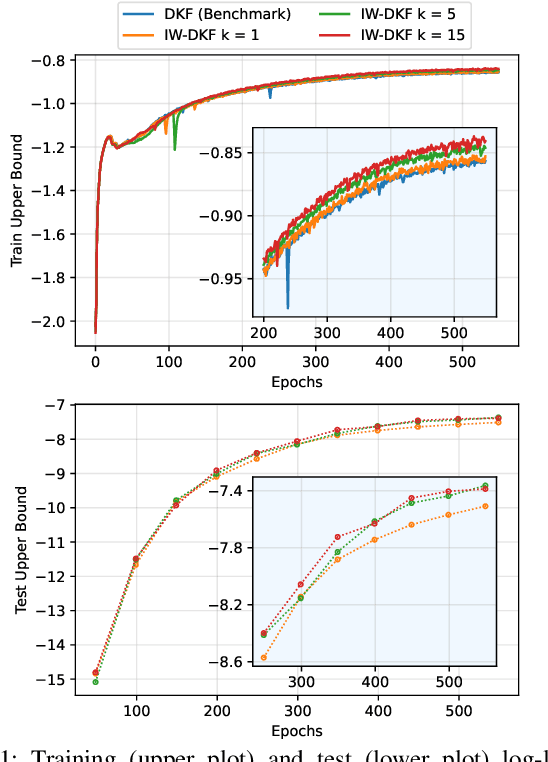
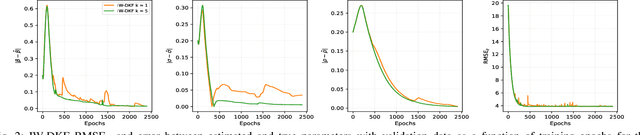
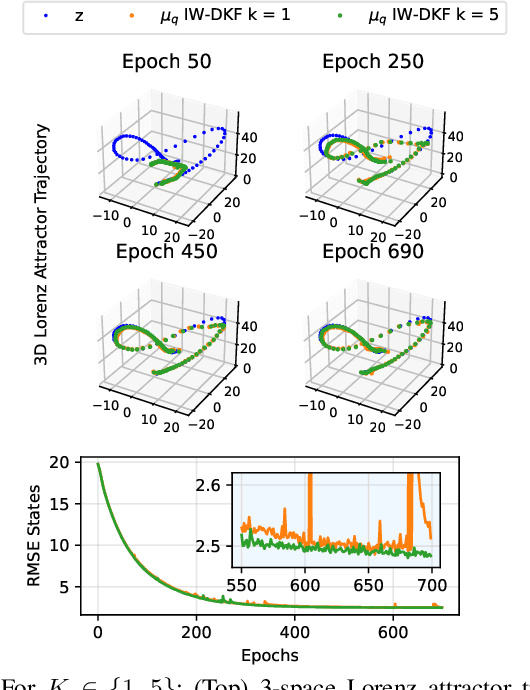
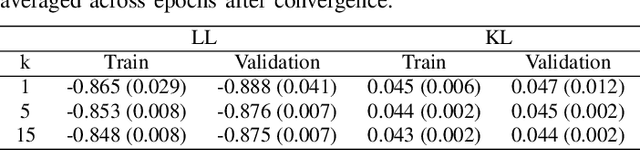
State inference and parameter learning in sequential models can be successfully performed with approximation techniques that maximize the evidence lower bound to the marginal log-likelihood of the data distribution. These methods may be referred to as Dynamical Variational Autoencoders, and our specific focus lies on the deep Kalman filter. It has been shown that the ELBO objective can oversimplify data representations, potentially compromising estimation quality. Tighter Monte Carlo objectives have been proposed in the literature to enhance generative modeling performance. For instance, the IWAE objective uses importance weights to reduce the variance of marginal log-likelihood estimates. In this paper, importance sampling is applied to the DKF framework for learning deep Markov models, resulting in the IW-DKF, which shows an improvement in terms of log-likelihood estimates and KL divergence between the variational distribution and the transition model. The framework using the sampled DKF update rule is also accommodated to address sequential state and parameter estimation when working with highly non-linear physics-based models. An experiment with the 3-space Lorenz attractor shows an enhanced generative modeling performance and also a decrease in RMSE when estimating the model parameters and latent states, indicating that tighter MCOs lead to improved state inference performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge