Hierarchical Homogeneity-Based Superpixel Segmentation: Application to Hyperspectral Image Analysis

Hyperspectral image (HI) analysis approaches have recently become increasingly complex and sophisticated. Recently, the combination of spectral-spatial information and superpixel techniques have addressed some hyperspectral data issues, such as the higher spatial variability of spectral signatures and dimensionality of the data. However, most existing superpixel approaches do not account for specific HI characteristics resulting from its high spectral dimension. In this work, we propose a multiscale superpixel method that is computationally efficient for processing hyperspectral data. The Simple Linear Iterative Clustering (SLIC) oversegmentation algorithm, on which the technique is based, has been extended hierarchically. Using a novel robust homogeneity testing, the proposed hierarchical approach leads to superpixels of variable sizes but with higher spectral homogeneity when compared to the classical SLIC segmentation. For validation, the proposed homogeneity-based hierarchical method was applied as a preprocessing step in the spectral unmixing and classification tasks carried out using, respectively, the Multiscale sparse Unmixing Algorithm (MUA) and the CNN-Enhanced Graph Convolutional Network (CEGCN) methods. Simulation results with both synthetic and real data show that the technique is competitive with state-of-the-art solutions.

A Generalized Multiscale Bundle-Based Hyperspectral Sparse Unmixing Algorithm

In hyperspectral sparse unmixing, a successful approach employs spectral bundles to address the variability of the endmembers in the spatial domain. However, the regularization penalties usually employed aggregate substantial computational complexity, and the solutions are very noise-sensitive. We generalize a multiscale spatial regularization approach to solve the unmixing problem by incorporating group sparsity-inducing mixed norms. Then, we propose a noise-robust method that can take advantage of the bundle structure to deal with endmember variability while ensuring inter- and intra-class sparsity in abundance estimation with reasonable computational cost. We also present a general heuristic to select the \emph{most representative} abundance estimation over multiple runs of the unmixing process, yielding a solution that is robust and highly reproducible. Experiments illustrate the robustness and consistency of the results when compared to related methods.

Model-Based Deep Autoencoder Networks for Nonlinear Hyperspectral Unmixing

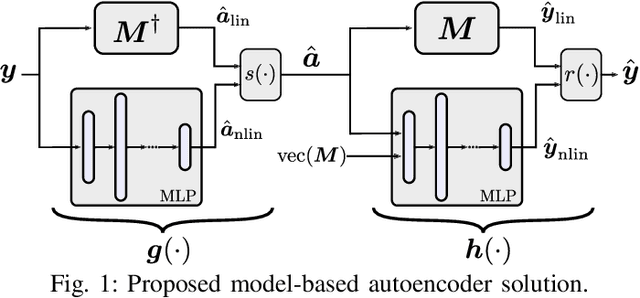
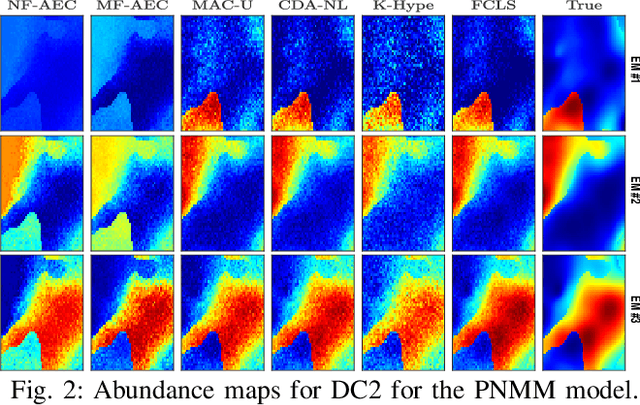
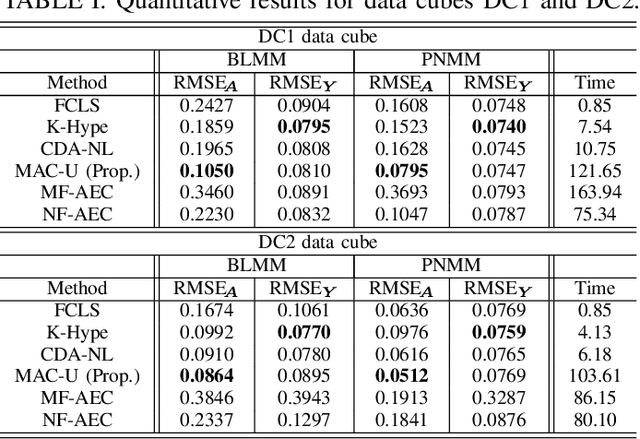
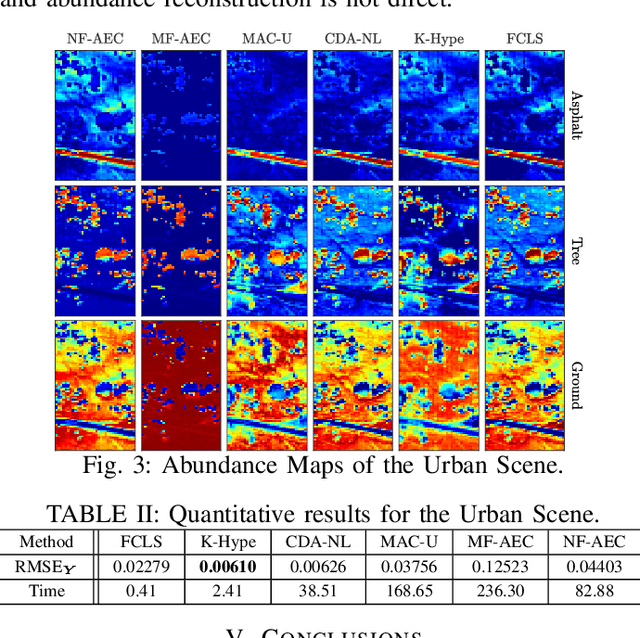
Autoencoder (AEC) networks have recently emerged as a promising approach to perform unsupervised hyperspectral unmixing (HU) by associating the latent representations with the abundances, the decoder with the mixing model and the encoder with its inverse. AECs are especially appealing for nonlinear HU since they lead to unsupervised and model-free algorithms. However, existing approaches fail to explore the fact that the encoder should invert the mixing process, which might reduce their robustness. In this paper, we propose a model-based AEC for nonlinear HU by considering the mixing model a nonlinear fluctuation over a linear mixture. Differently from previous works, we show that this restriction naturally imposes a particular structure to both the encoder and to the decoder networks. This introduces prior information in the AEC without reducing the flexibility of the mixing model. Simulations with synthetic and real data indicate that the proposed strategy improves nonlinear HU.

Fast Unmixing and Change Detection in Multitemporal Hyperspectral Data

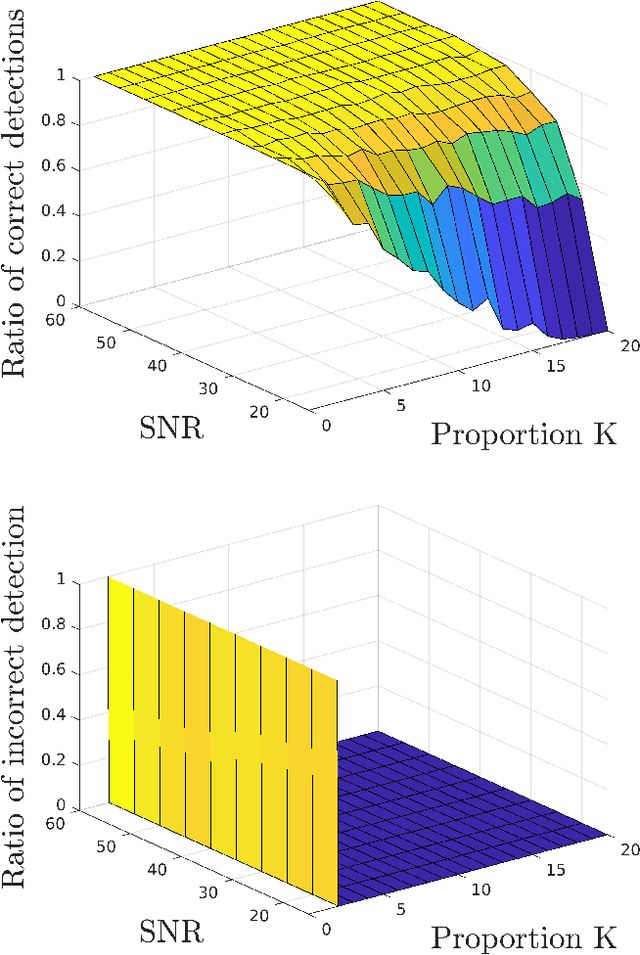
Multitemporal spectral unmixing (SU) is a powerful tool to process hyperspectral image (HI) sequences due to its ability to reveal the evolution of materials over time and space in a scene. However, significant spectral variability is often observed between collection of images due to variations in acquisition or seasonal conditions. This characteristic has to be considered in the design of SU algorithms. Because of its good performance, the multiple endmember spectral mixture analysis algorithm (MESMA) has been recently used to perform SU in multitemporal scenarios arising in several practical applications. However, MESMA does not consider the relationship between the different HIs, and its computational complexity is extremely high for large spectral libraries. In this work, we propose an efficient multitemporal SU method that exploits the high temporal correlation between the abundances to provide more accurate results at a lower computational complexity. We propose to solve the complex general multitemporal SU problem by separately addressing the endmember selection and the abundance estimation problems. This leads to a simpler solution without sacrificing the accuracy of the results. We also propose a strategy to detect and address abrupt abundance variations. Theoretical results demonstrate how the proposed method compares to MESMA in terms of quality, and how effective it is in detecting abundance changes. This analysis provides valuable insight into the conditions under which the algorithm succeeds. Simulation results show that the proposed method achieves state-of-the-art performance at a smaller computational cost.

Kalman Filtering and Expectation Maximization for Multitemporal Spectral Unmixing

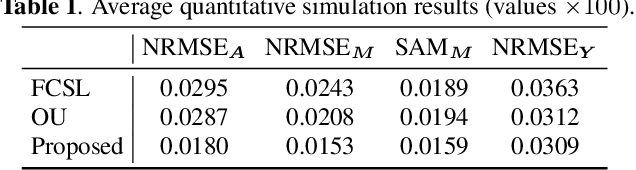
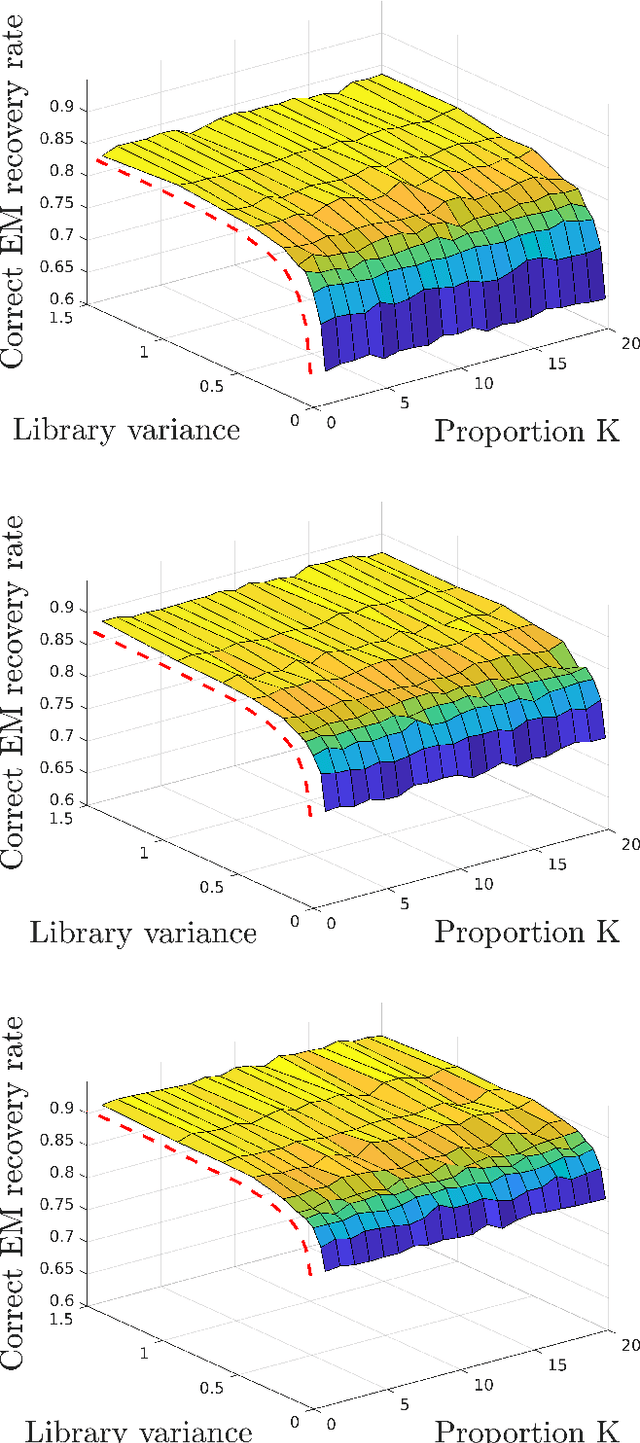
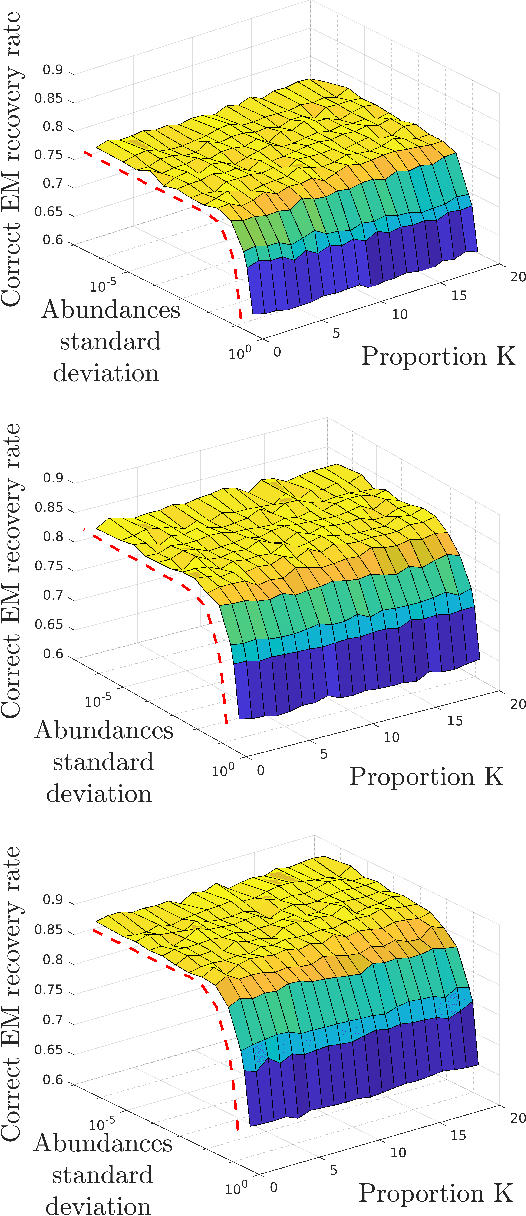
The recent evolution of hyperspectral imaging technology and the proliferation of new emerging applications presses for the processing of multiple temporal hyperspectral images. In this work, we propose a novel spectral unmixing (SU) strategy using physically motivated parametric endmember representations to account for temporal spectral variability. By representing the multitemporal mixing process using a state-space formulation, we are able to exploit the Bayesian filtering machinery to estimate the endmember variability coefficients. Moreover, by assuming that the temporal variability of the abundances is small over short intervals, an efficient implementation of the expectation maximization (EM) algorithm is employed to estimate the abundances and the other model parameters. Simulation results indicate that the proposed strategy outperforms state-of-the-art multitemporal SU algorithms.

Deep Generative Models for Library Augmentation in Multiple Endmember Spectral Mixture Analysis

Multiple Endmember Spectral Mixture Analysis (MESMA) is one of the leading approaches to perform spectral unmixing (SU) considering variability of the endmembers (EMs). It represents each endmember in the image using libraries of spectral signatures acquired a priori. However, existing spectral libraries are often small and unable to properly capture the variability of each endmember in practical scenes, what significantly compromises the performance of MESMA. In this paper, we propose a library augmentation strategy to improve the diversity of existing spectral libraries, thus improving their ability to represent the materials in real images. First, the proposed methodology leverages the power of deep generative models (DGMs) to learn the statistical distribution of the endmembers based on the spectral signatures available in the existing libraries. Afterwards, new samples can be drawn from the learned EM distributions and used to augment the spectral libraries, improving the overall quality of the unmixing process. Experimental results using synthetic and real data attest the superior performance of the proposed method even under library mismatch conditions.

A Blind Multiscale Spatial Regularization Framework for Kernel-based Spectral Unmixing

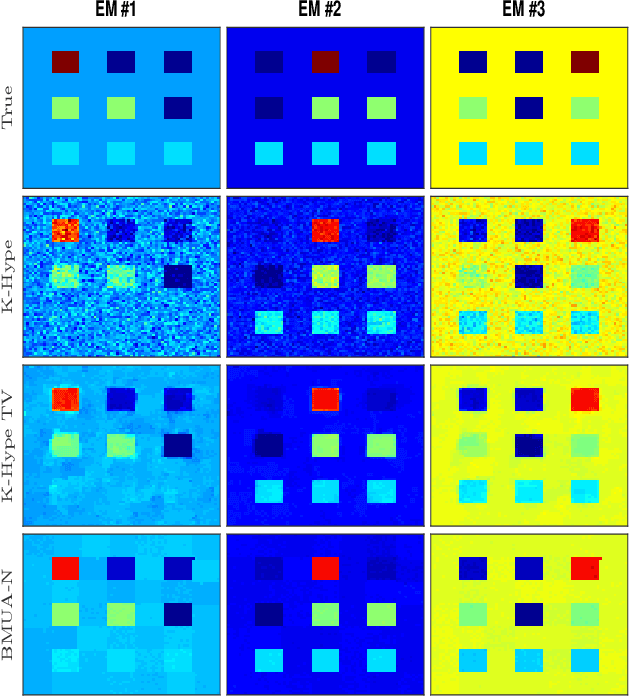
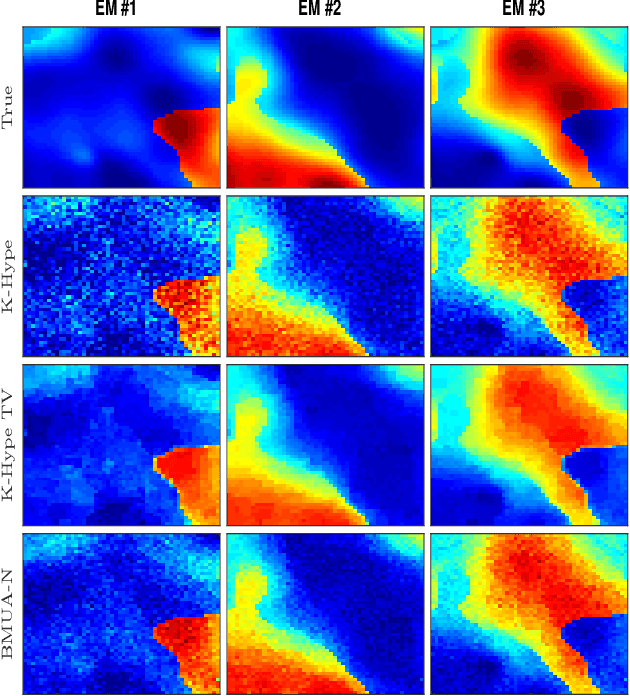
Introducing spatial prior information in hyperspectral imaging (HSI) analysis has led to an overall improvement of the performance of many HSI methods applied for denoising, classification, and unmixing. Extending such methodologies to nonlinear settings is not always straightforward, specially for unmixing problems where the consideration of spatial relationships between neighboring pixels might comprise intricate interactions between their fractional abundances and nonlinear contributions. In this paper, we consider a multiscale regularization strategy for nonlinear spectral unmixing with kernels. The proposed methodology splits the unmixing problem into two sub-problems at two different spatial scales: a coarse scale containing low-dimensional structures, and the original fine scale. The coarse spatial domain is defined using superpixels that result from a multiscale transformation. Spectral unmixing is then formulated as the solution of quadratically constrained optimization problems, which are solved efficiently by exploring a reformulation of their dual cost functions in the form of root-finding problems. Furthermore, we employ a theory-based statistical framework to devise a consistent strategy to estimate all required parameters, including both the regularization parameters of the algorithm and the number of superpixels of the transformation, resulting in a truly blind (from the parameters setting perspective) unmixing method. Experimental results attest the superior performance of the proposed method when comparing with other, state-of-the-art, related strategies.

Deep Generative Endmember Modeling: An Application to Unsupervised Spectral Unmixing

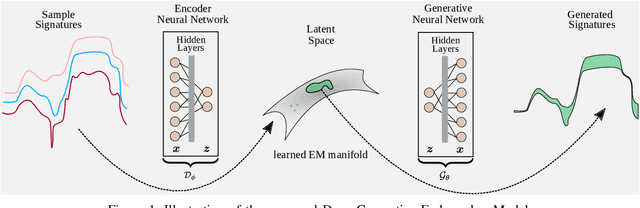
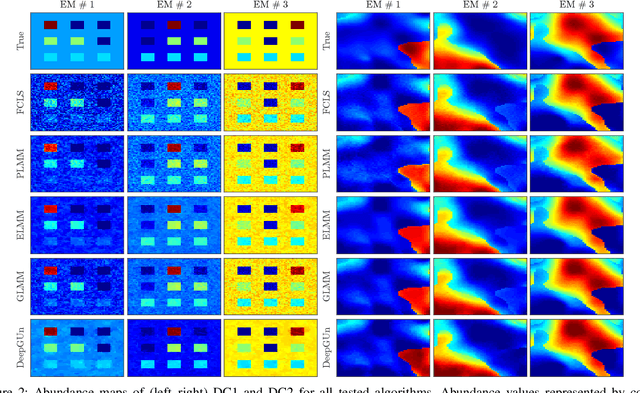
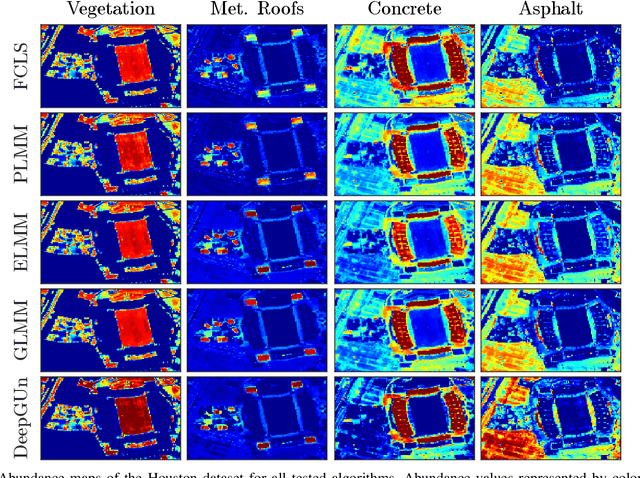
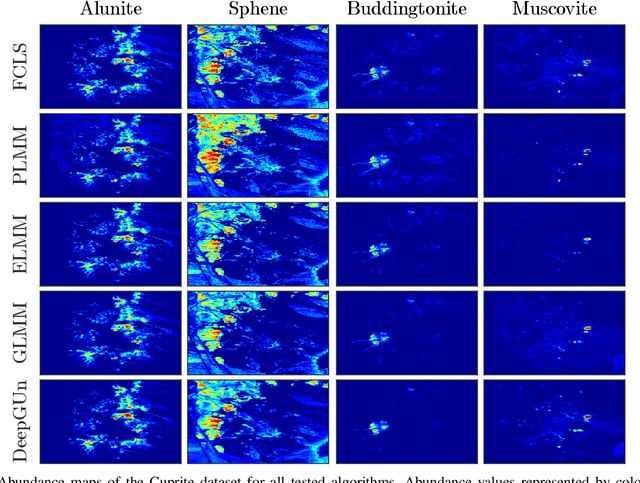
Endmember (EM) spectral variability can greatly impact the performance of standard hyperspectral image analysis algorithms. Extended parametric models have been successfully applied to account for the EM spectral variability. However, these models still lack the compromise between flexibility and low-dimensional representation that is necessary to properly explore the fact that spectral variability is often confined to a low-dimensional manifold in real scenes. In this paper we propose to learn a spectral variability model directly form the observed data, instead of imposing it \emph{a priori}. This is achieved through a deep generative EM model, which is estimated using a variational autoencoder (VAE). The encoder and decoder that compose the generative model are trained using pure pixel information extracted directly from the observed image, what allows for an unsupervised formulation. The proposed EM model is applied to the solution of a spectral unmixing problem, which we cast as an alternating nonlinear least-squares problem that is solved iteratively with respect to the abundances and to the low-dimensional representations of the EMs in the latent space of the deep generative model. Simulations using both synthetic and real data indicate that the proposed strategy can outperform the competing state-of-the-art algorithms.

Improved Hyperspectral Unmixing With Endmember Variability Parametrized Using an Interpolated Scaling Tensor

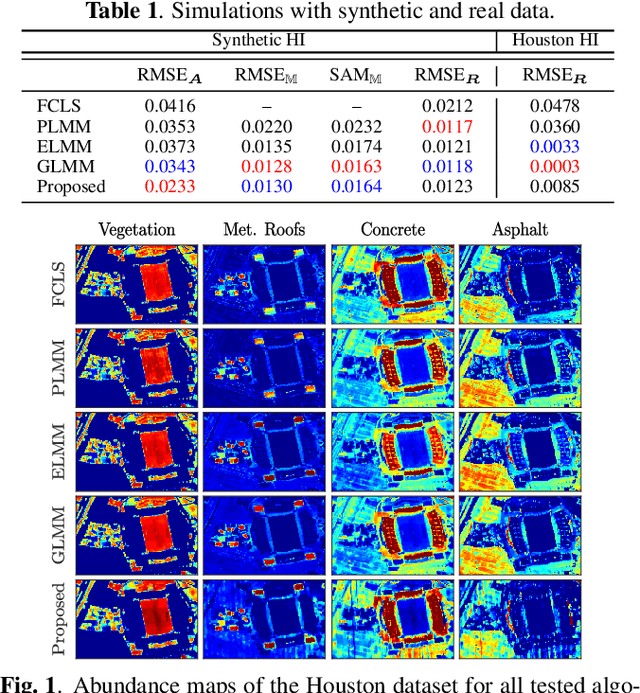
Endmember (EM) variability has an important impact on the performance of hyperspectral image (HI) analysis algorithms. Recently, extended linear mixing models have been proposed to account for EM variability in the spectral unmixing (SU) problem. The direct use of these models has led to severely ill-posed optimization problems. Different regularization strategies have been considered to deal with this issue, but none so far has consistently exploited the information provided by the existence of multiple pure pixels often present in HIs. In this work, we propose to break the SU problem into a sequence of two problems. First, we use pure pixel information to estimate an interpolated tensor of scaling factors representing spectral variability. This is done by considering the spectral variability to be a smooth function over the HI and confining the energy of the scaling tensor to a low-rank structure. Afterwards, we solve a matrix-factorization problem to estimate the fractional abundances using the variability scaling factors estimated in the previous step, what leads to a significantly more well-posed problem. Simulation swith synthetic and real data attest the effectiveness of the proposed strategy.

Low-Rank Tensor Modeling for Hyperspectral Unmixing Accounting for Spectral Variability

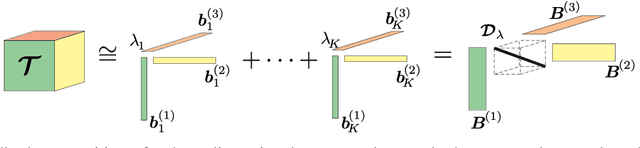
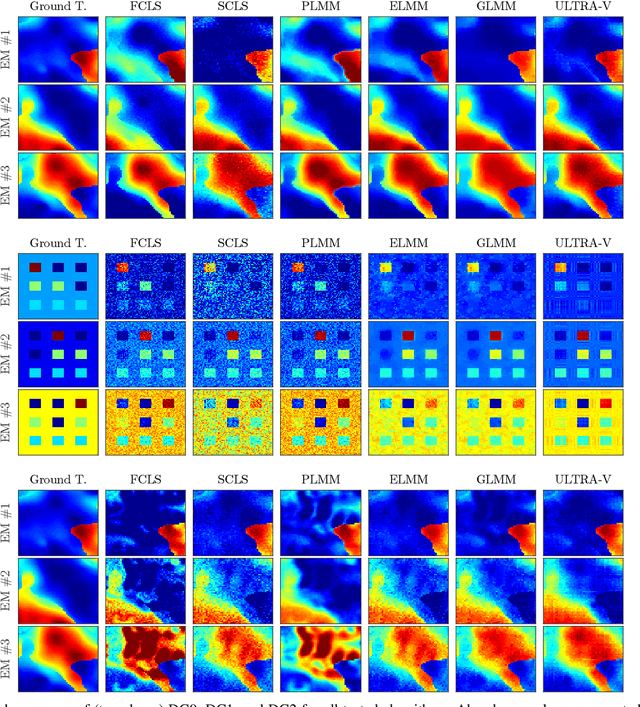
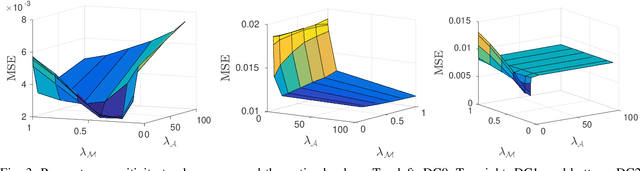
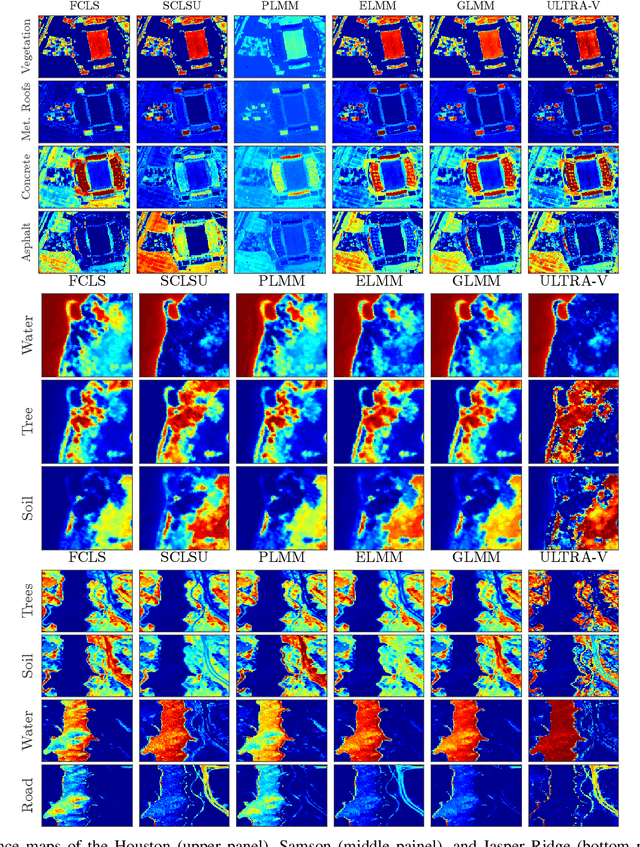
Traditional hyperspectral unmixing methods neglect the underlying variability of spectral signatures often obeserved in typical hyperspectral images, propagating these missmodeling errors throughout the whole unmixing process. Attempts to model material spectra as members of sets or as random variables tend to lead to severely ill-posed unmixing problems. To overcome this drawback, endmember variability has been handled through generalizations of the mixing model, combined with spatial regularization over the abundance and endmember estimations. Recently, tensor-based strategies considered low-rank decompositions of hyperspectral images as an alternative to impose low-dimensional structures on the solutions of standard and multitemporal unmixing problems. These strategies, however, present two main drawbacks: 1) they confine the solutions to low-rank tensors, which often cannot represent the complexity of real-world scenarios; and 2) they lack guarantees that endmembers and abundances will be correctly factorized in their respective tensors. In this work, we propose a more flexible approach, called ULTRA-V, that imposes low-rank structures through regularizations whose strictness is controlled by scalar parameters. Simulations attest the superior accuracy of the method when compared with state-of-the-art unmixing algorithms that account for spectral variability.