A Blind Multiscale Spatial Regularization Framework for Kernel-based Spectral Unmixing

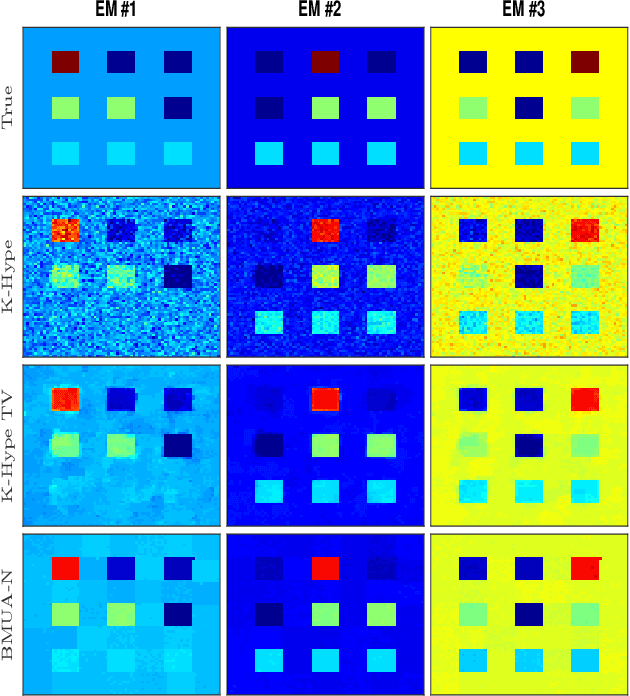
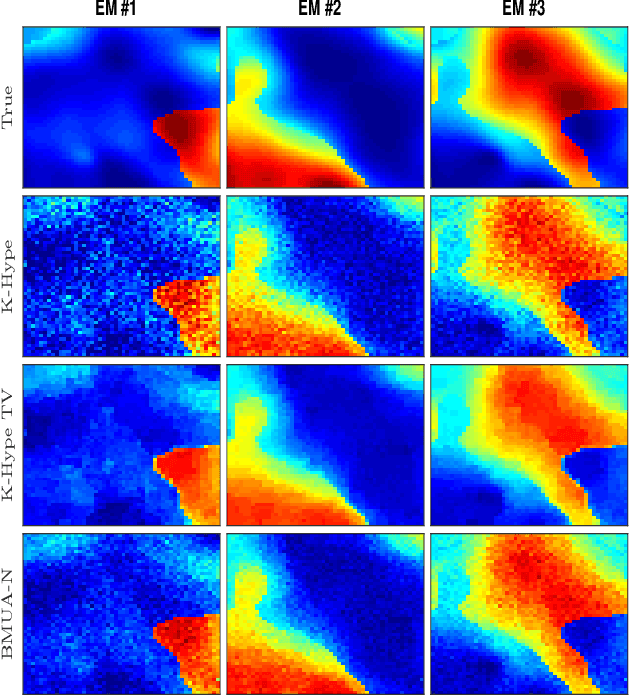
Introducing spatial prior information in hyperspectral imaging (HSI) analysis has led to an overall improvement of the performance of many HSI methods applied for denoising, classification, and unmixing. Extending such methodologies to nonlinear settings is not always straightforward, specially for unmixing problems where the consideration of spatial relationships between neighboring pixels might comprise intricate interactions between their fractional abundances and nonlinear contributions. In this paper, we consider a multiscale regularization strategy for nonlinear spectral unmixing with kernels. The proposed methodology splits the unmixing problem into two sub-problems at two different spatial scales: a coarse scale containing low-dimensional structures, and the original fine scale. The coarse spatial domain is defined using superpixels that result from a multiscale transformation. Spectral unmixing is then formulated as the solution of quadratically constrained optimization problems, which are solved efficiently by exploring a reformulation of their dual cost functions in the form of root-finding problems. Furthermore, we employ a theory-based statistical framework to devise a consistent strategy to estimate all required parameters, including both the regularization parameters of the algorithm and the number of superpixels of the transformation, resulting in a truly blind (from the parameters setting perspective) unmixing method. Experimental results attest the superior performance of the proposed method when comparing with other, state-of-the-art, related strategies.