Improved Hyperspectral Unmixing With Endmember Variability Parametrized Using an Interpolated Scaling Tensor

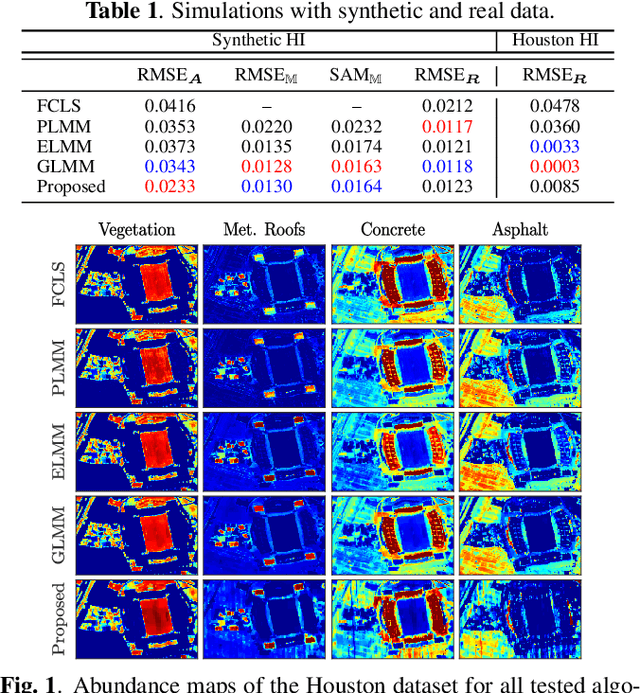
Endmember (EM) variability has an important impact on the performance of hyperspectral image (HI) analysis algorithms. Recently, extended linear mixing models have been proposed to account for EM variability in the spectral unmixing (SU) problem. The direct use of these models has led to severely ill-posed optimization problems. Different regularization strategies have been considered to deal with this issue, but none so far has consistently exploited the information provided by the existence of multiple pure pixels often present in HIs. In this work, we propose to break the SU problem into a sequence of two problems. First, we use pure pixel information to estimate an interpolated tensor of scaling factors representing spectral variability. This is done by considering the spectral variability to be a smooth function over the HI and confining the energy of the scaling tensor to a low-rank structure. Afterwards, we solve a matrix-factorization problem to estimate the fractional abundances using the variability scaling factors estimated in the previous step, what leads to a significantly more well-posed problem. Simulation swith synthetic and real data attest the effectiveness of the proposed strategy.