Privacy Preserving Semi-Decentralized Mean Estimation over Intermittently-Connected Networks

We consider the problem of privately estimating the mean of vectors distributed across different nodes of an unreliable wireless network, where communications between nodes can fail intermittently. We adopt a semi-decentralized setup, wherein to mitigate the impact of intermittently connected links, nodes can collaborate with their neighbors to compute a local consensus, which they relay to a central server. In such a setting, the communications between any pair of nodes must ensure that the privacy of the nodes is rigorously maintained to prevent unauthorized information leakage. We study the tradeoff between collaborative relaying and privacy leakage due to the data sharing among nodes and, subsequently, propose PriCER: Private Collaborative Estimation via Relaying -- a differentially private collaborative algorithm for mean estimation to optimize this tradeoff. The privacy guarantees of PriCER arise (i) implicitly, by exploiting the inherent stochasticity of the flaky network connections, and (ii) explicitly, by adding Gaussian perturbations to the estimates exchanged by the nodes. Local and central privacy guarantees are provided against eavesdroppers who can observe different signals, such as the communications amongst nodes during local consensus and (possibly multiple) transmissions from the relays to the central server. We substantiate our theoretical findings with numerical simulations. Our implementation is available at https://github.com/rajarshisaha95/private-collaborative-relaying.

Compressing Large Language Models using Low Rank and Low Precision Decomposition

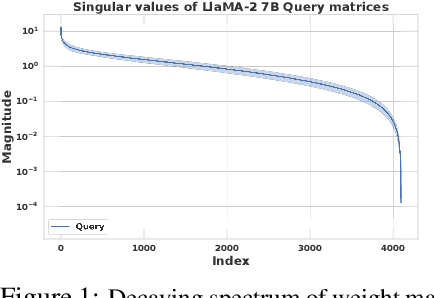
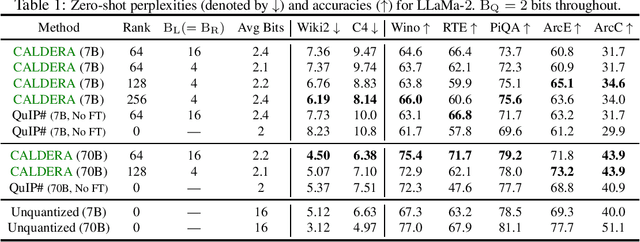
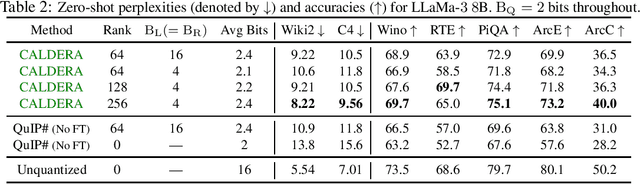
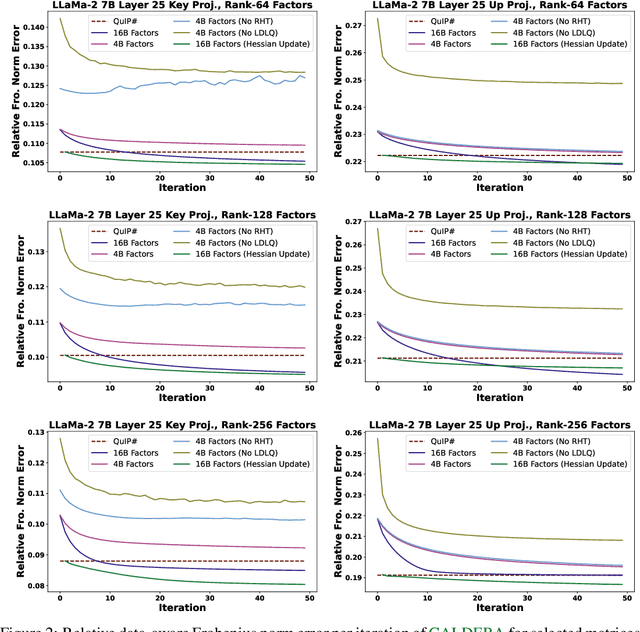
The prohibitive sizes of Large Language Models (LLMs) today make it difficult to deploy them on memory-constrained edge devices. This work introduces $\rm CALDERA$ -- a new post-training LLM compression algorithm that harnesses the inherent low-rank structure of a weight matrix $\mathbf{W}$ by approximating it via a low-rank, low-precision decomposition as $\mathbf{W} \approx \mathbf{Q} + \mathbf{L}\mathbf{R}$. Here, $\mathbf{L}$ and $\mathbf{R}$ are low rank factors, and the entries of $\mathbf{Q}$, $\mathbf{L}$ and $\mathbf{R}$ are quantized. The model is compressed by substituting each layer with its $\mathbf{Q} + \mathbf{L}\mathbf{R}$ decomposition, and the zero-shot performance of the compressed model is evaluated. Additionally, $\mathbf{L}$ and $\mathbf{R}$ are readily amenable to low-rank adaptation, consequently enhancing the zero-shot performance. $\rm CALDERA$ obtains this decomposition by formulating it as an optimization problem $\min_{\mathbf{Q},\mathbf{L},\mathbf{R}}\lVert(\mathbf{Q} + \mathbf{L}\mathbf{R} - \mathbf{W})\mathbf{X}^\top\rVert_{\rm F}^2$, where $\mathbf{X}$ is the calibration data, and $\mathbf{Q}, \mathbf{L}, \mathbf{R}$ are constrained to be representable using low-precision formats. Theoretical upper bounds on the approximation error of $\rm CALDERA$ are established using a rank-constrained regression framework, and the tradeoff between compression ratio and model performance is studied by analyzing the impact of target rank and quantization bit budget. Results illustrate that compressing LlaMa-$2$ $7$B/$70$B and LlaMa-$3$ $8$B models obtained using $\rm CALDERA$ outperforms existing post-training LLM compression techniques in the regime of less than $2.5$ bits per parameter. The implementation is available at: \href{https://github.com/pilancilab/caldera}{https://github.com/pilancilab/caldera}.

Matrix Compression via Randomized Low Rank and Low Precision Factorization

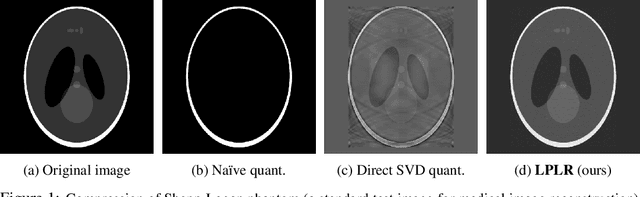
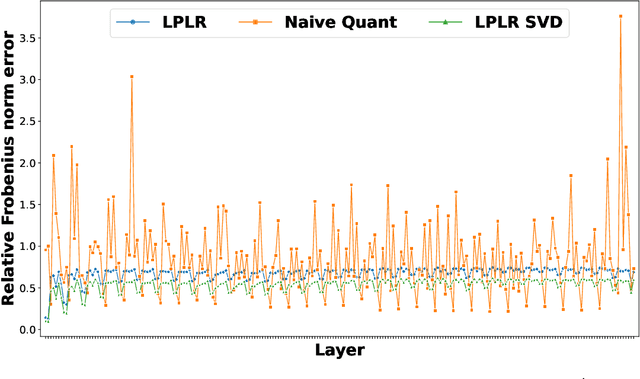
Matrices are exceptionally useful in various fields of study as they provide a convenient framework to organize and manipulate data in a structured manner. However, modern matrices can involve billions of elements, making their storage and processing quite demanding in terms of computational resources and memory usage. Although prohibitively large, such matrices are often approximately low rank. We propose an algorithm that exploits this structure to obtain a low rank decomposition of any matrix $\mathbf{A}$ as $\mathbf{A} \approx \mathbf{L}\mathbf{R}$, where $\mathbf{L}$ and $\mathbf{R}$ are the low rank factors. The total number of elements in $\mathbf{L}$ and $\mathbf{R}$ can be significantly less than that in $\mathbf{A}$. Furthermore, the entries of $\mathbf{L}$ and $\mathbf{R}$ are quantized to low precision formats $--$ compressing $\mathbf{A}$ by giving us a low rank and low precision factorization. Our algorithm first computes an approximate basis of the range space of $\mathbf{A}$ by randomly sketching its columns, followed by a quantization of the vectors constituting this basis. It then computes approximate projections of the columns of $\mathbf{A}$ onto this quantized basis. We derive upper bounds on the approximation error of our algorithm, and analyze the impact of target rank and quantization bit-budget. The tradeoff between compression ratio and approximation accuracy allows for flexibility in choosing these parameters based on specific application requirements. We empirically demonstrate the efficacy of our algorithm in image compression, nearest neighbor classification of image and text embeddings, and compressing the layers of LlaMa-$7$b. Our results illustrate that we can achieve compression ratios as aggressive as one bit per matrix coordinate, all while surpassing or maintaining the performance of traditional compression techniques.

Collaborative Mean Estimation over Intermittently Connected Networks with Peer-To-Peer Privacy

This work considers the problem of Distributed Mean Estimation (DME) over networks with intermittent connectivity, where the goal is to learn a global statistic over the data samples localized across distributed nodes with the help of a central server. To mitigate the impact of intermittent links, nodes can collaborate with their neighbors to compute local consensus which they forward to the central server. In such a setup, the communications between any pair of nodes must satisfy local differential privacy constraints. We study the tradeoff between collaborative relaying and privacy leakage due to the additional data sharing among nodes and, subsequently, propose a novel differentially private collaborative algorithm for DME to achieve the optimal tradeoff. Finally, we present numerical simulations to substantiate our theoretical findings.

Semi-Decentralized Federated Learning with Collaborative Relaying

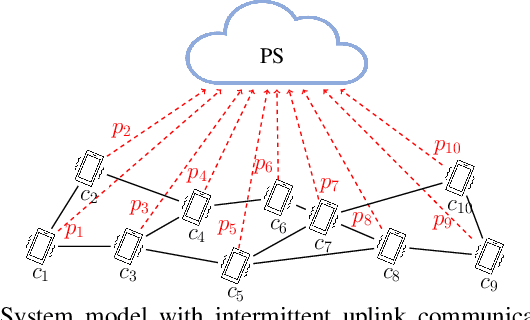
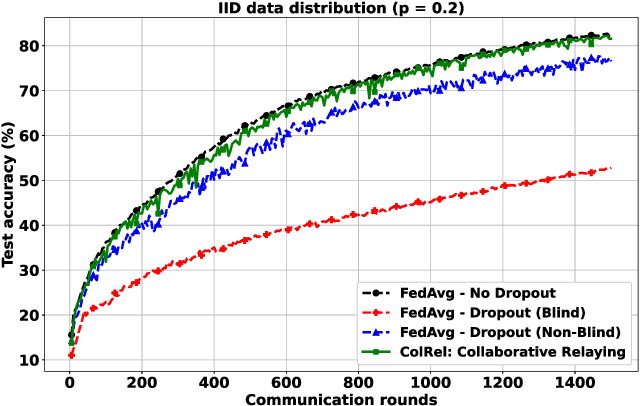
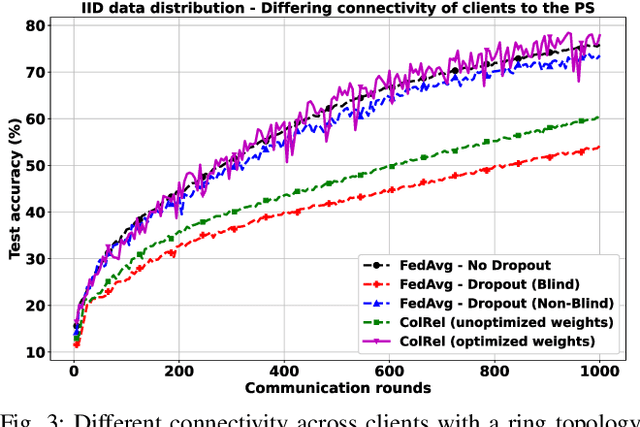
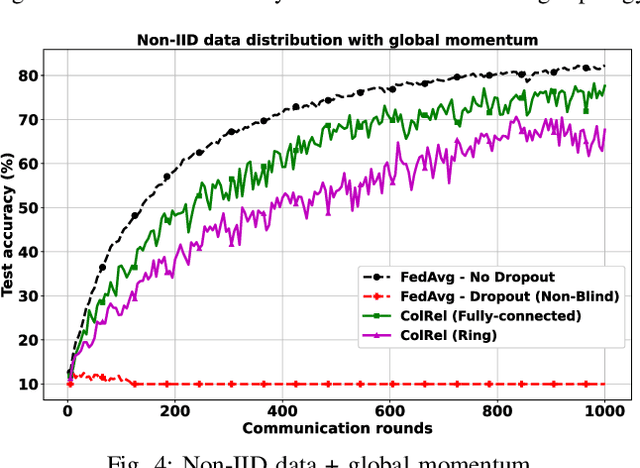
We present a semi-decentralized federated learning algorithm wherein clients collaborate by relaying their neighbors' local updates to a central parameter server (PS). At every communication round to the PS, each client computes a local consensus of the updates from its neighboring clients and eventually transmits a weighted average of its own update and those of its neighbors to the PS. We appropriately optimize these averaging weights to ensure that the global update at the PS is unbiased and to reduce the variance of the global update at the PS, consequently improving the rate of convergence. Numerical simulations substantiate our theoretical claims and demonstrate settings with intermittent connectivity between the clients and the PS, where our proposed algorithm shows an improved convergence rate and accuracy in comparison with the federated averaging algorithm.

Robust Federated Learning with Connectivity Failures: A Semi-Decentralized Framework with Collaborative Relaying

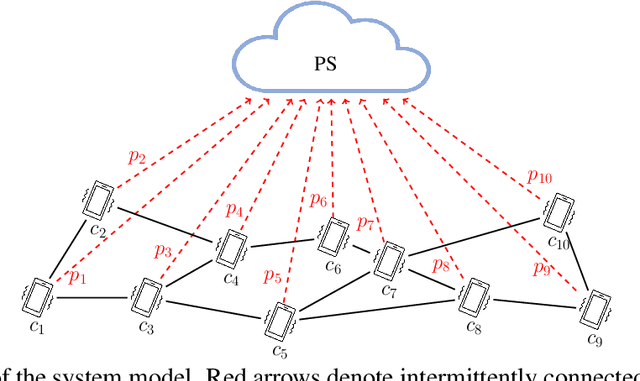
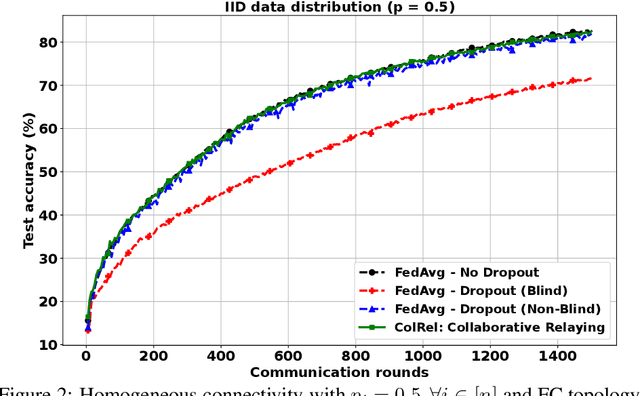
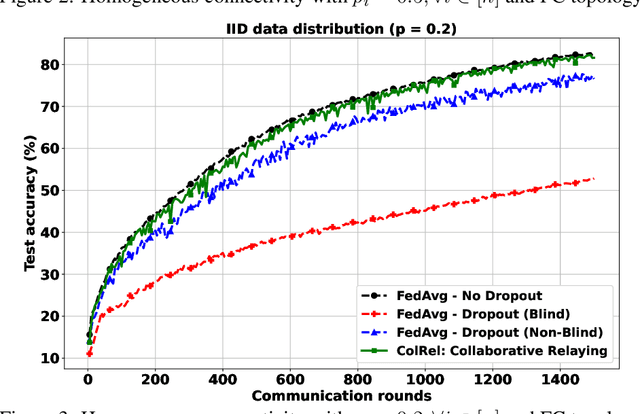
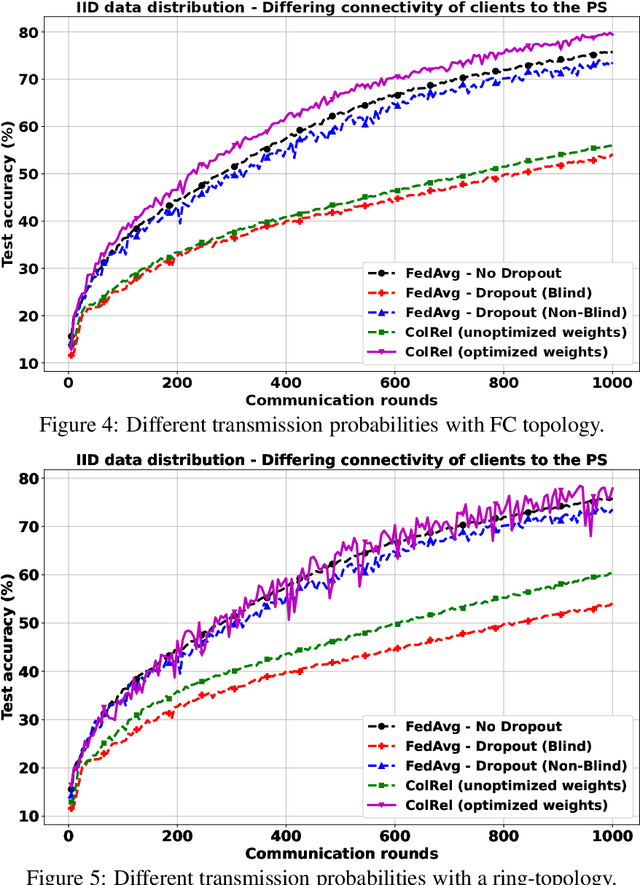
Intermittent client connectivity is one of the major challenges in centralized federated edge learning frameworks. Intermittently failing uplinks to the central parameter server (PS) can induce a large generalization gap in performance especially when the data distribution among the clients exhibits heterogeneity. In this work, to mitigate communication blockages between clients and the central PS, we introduce the concept of knowledge relaying wherein the successfully participating clients collaborate in relaying their neighbors' local updates to a central parameter server (PS) in order to boost the participation of clients with intermittently failing connectivity. We propose a collaborative relaying based semi-decentralized federated edge learning framework where at every communication round each client first computes a local consensus of the updates from its neighboring clients and eventually transmits a weighted average of its own update and those of its neighbors to the PS. We appropriately optimize these averaging weights to reduce the variance of the global update at the PS while ensuring that the global update is unbiased, consequently improving the convergence rate. Finally, by conducting experiments on CIFAR-10 dataset we validate our theoretical results and demonstrate that our proposed scheme is superior to Federated averaging benchmark especially when data distribution among clients is non-iid.

Minimax Optimal Quantization of Linear Models: Information-Theoretic Limits and Efficient Algorithms

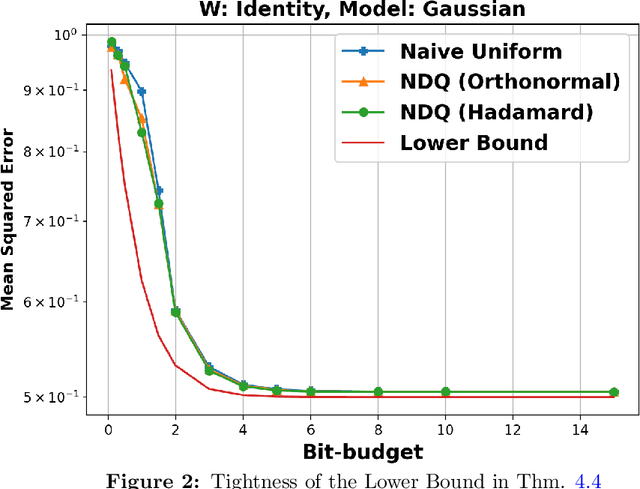
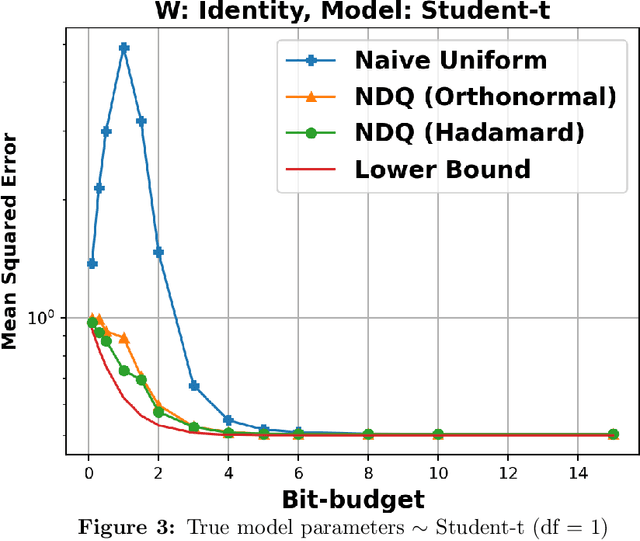
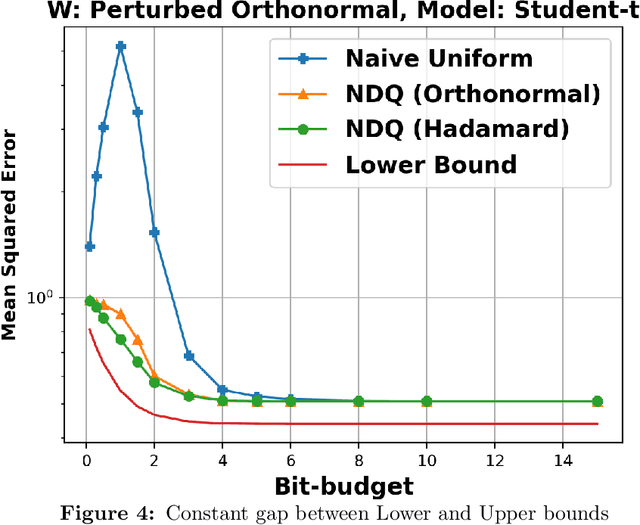
We consider the problem of quantizing a linear model learned from measurements $\mathbf{X} = \mathbf{W}\boldsymbol{\theta} + \mathbf{v}$. The model is constrained to be representable using only $dB$-bits, where $B \in (0, \infty)$ is a pre-specified budget and $d$ is the dimension of the model. We derive an information-theoretic lower bound for the minimax risk under this setting and show that it is tight with a matching upper bound. This upper bound is achieved using randomized embedding based algorithms. We propose randomized Hadamard embeddings that are computationally efficient while performing near-optimally. We also show that our method and upper-bounds can be extended for two-layer ReLU neural networks. Numerical simulations validate our theoretical claims.

Partner-Aware Algorithms in Decentralized Cooperative Bandit Teams

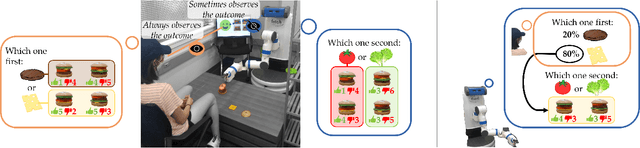
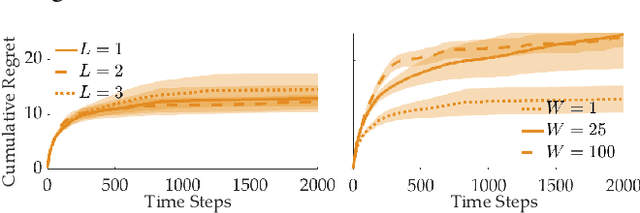
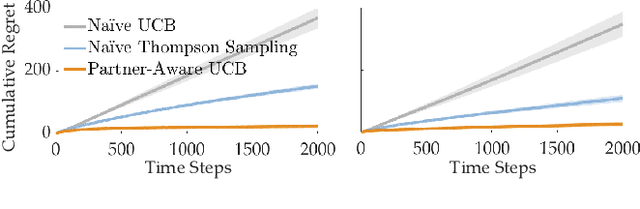
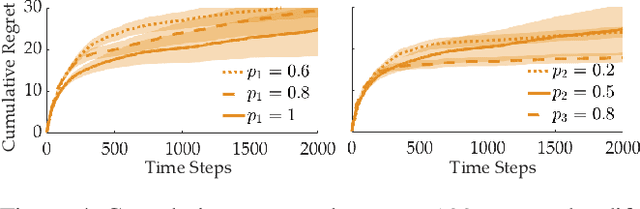
When humans collaborate with each other, they often make decisions by observing others and considering the consequences that their actions may have on the entire team, instead of greedily doing what is best for just themselves. We would like our AI agents to effectively collaborate in a similar way by capturing a model of their partners. In this work, we propose and analyze a decentralized Multi-Armed Bandit (MAB) problem with coupled rewards as an abstraction of more general multi-agent collaboration. We demonstrate that na\"ive extensions of single-agent optimal MAB algorithms fail when applied for decentralized bandit teams. Instead, we propose a Partner-Aware strategy for joint sequential decision-making that extends the well-known single-agent Upper Confidence Bound algorithm. We analytically show that our proposed strategy achieves logarithmic regret, and provide extensive experiments involving human-AI and human-robot collaboration to validate our theoretical findings. Our results show that the proposed partner-aware strategy outperforms other known methods, and our human subject studies suggest humans prefer to collaborate with AI agents implementing our partner-aware strategy.

Distributed Learning and Democratic Embeddings: Polynomial-Time Source Coding Schemes Can Achieve Minimax Lower Bounds for Distributed Gradient Descent under Communication Constraints

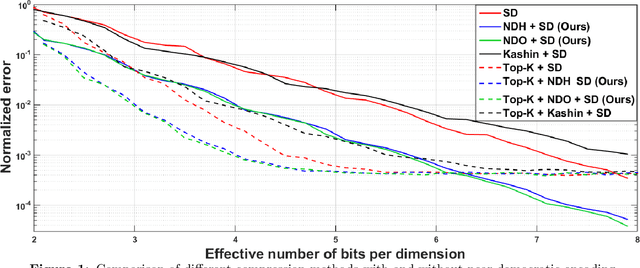
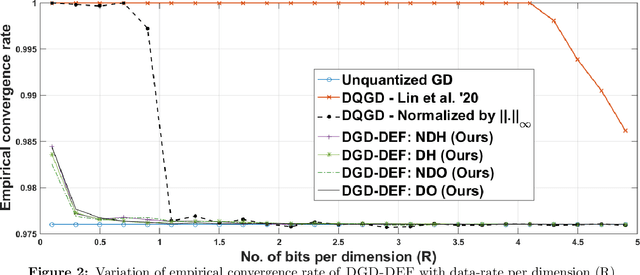
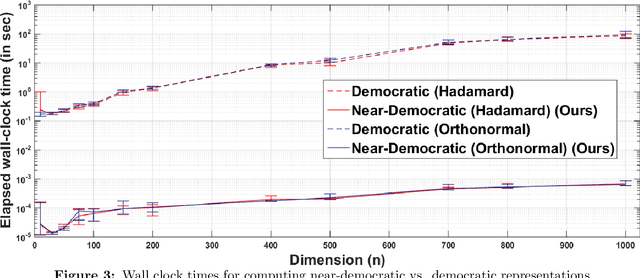
In this work, we consider the distributed optimization setting where information exchange between the computation nodes and the parameter server is subject to a maximum bit-budget. We first consider the problem of compressing a vector in the n-dimensional Euclidean space, subject to a bit-budget of R-bits per dimension, for which we introduce Democratic and Near-Democratic source-coding schemes. We show that these coding schemes are (near) optimal in the sense that the covering efficiency of the resulting quantizer is either dimension independent, or has a very weak logarithmic dependence. Subsequently, we propose a distributed optimization algorithm: DGD-DEF, which employs our proposed coding strategy, and achieves the minimax optimal convergence rate to within (near) constant factors for a class of communication-constrained distributed optimization algorithms. Furthermore, we extend the utility of our proposed source coding scheme by showing that it can remarkably improve the performance when used in conjunction with other compression schemes. We validate our theoretical claims through numerical simulations. Keywords: Fast democratic (Kashin) embeddings, Distributed optimization, Data-rate constraint, Quantized gradient descent, Error feedback.