Compressing Large Language Models using Low Rank and Low Precision Decomposition

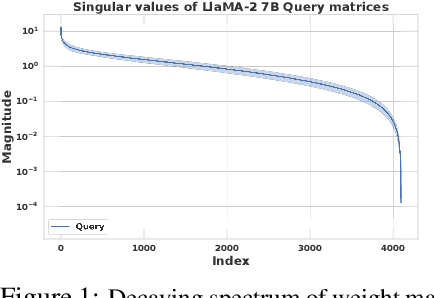
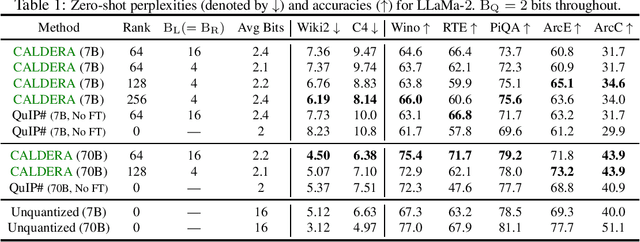
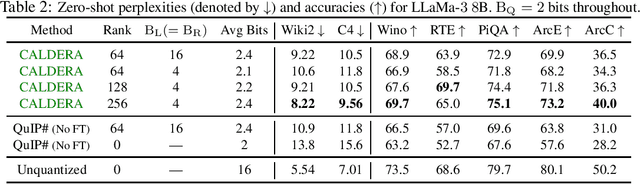
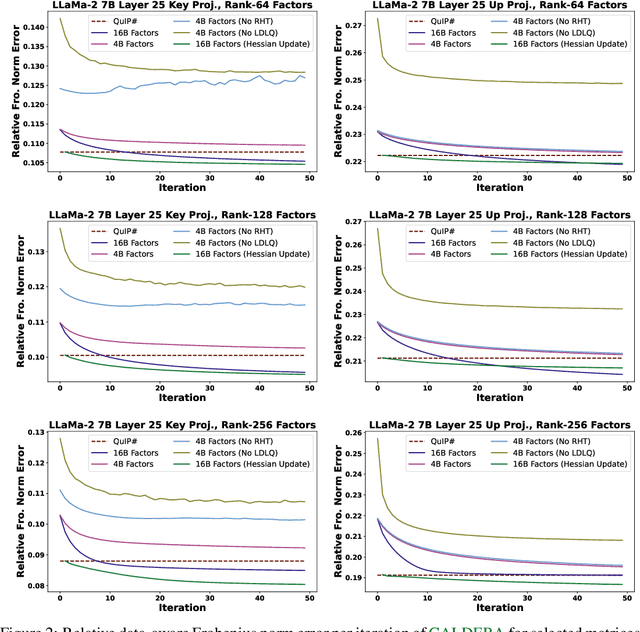
The prohibitive sizes of Large Language Models (LLMs) today make it difficult to deploy them on memory-constrained edge devices. This work introduces $\rm CALDERA$ -- a new post-training LLM compression algorithm that harnesses the inherent low-rank structure of a weight matrix $\mathbf{W}$ by approximating it via a low-rank, low-precision decomposition as $\mathbf{W} \approx \mathbf{Q} + \mathbf{L}\mathbf{R}$. Here, $\mathbf{L}$ and $\mathbf{R}$ are low rank factors, and the entries of $\mathbf{Q}$, $\mathbf{L}$ and $\mathbf{R}$ are quantized. The model is compressed by substituting each layer with its $\mathbf{Q} + \mathbf{L}\mathbf{R}$ decomposition, and the zero-shot performance of the compressed model is evaluated. Additionally, $\mathbf{L}$ and $\mathbf{R}$ are readily amenable to low-rank adaptation, consequently enhancing the zero-shot performance. $\rm CALDERA$ obtains this decomposition by formulating it as an optimization problem $\min_{\mathbf{Q},\mathbf{L},\mathbf{R}}\lVert(\mathbf{Q} + \mathbf{L}\mathbf{R} - \mathbf{W})\mathbf{X}^\top\rVert_{\rm F}^2$, where $\mathbf{X}$ is the calibration data, and $\mathbf{Q}, \mathbf{L}, \mathbf{R}$ are constrained to be representable using low-precision formats. Theoretical upper bounds on the approximation error of $\rm CALDERA$ are established using a rank-constrained regression framework, and the tradeoff between compression ratio and model performance is studied by analyzing the impact of target rank and quantization bit budget. Results illustrate that compressing LlaMa-$2$ $7$B/$70$B and LlaMa-$3$ $8$B models obtained using $\rm CALDERA$ outperforms existing post-training LLM compression techniques in the regime of less than $2.5$ bits per parameter. The implementation is available at: \href{https://github.com/pilancilab/caldera}{https://github.com/pilancilab/caldera}.

Matrix Compression via Randomized Low Rank and Low Precision Factorization

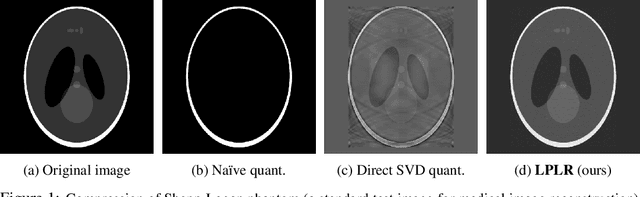
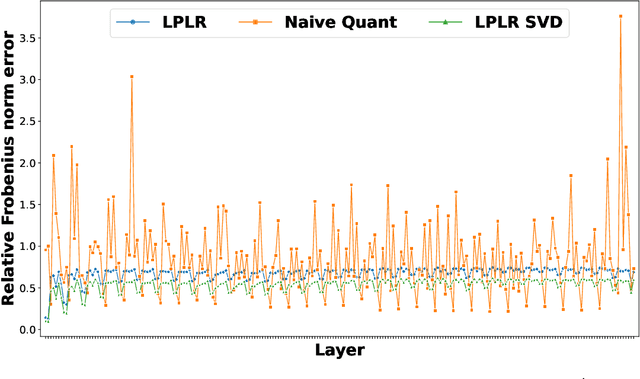
Matrices are exceptionally useful in various fields of study as they provide a convenient framework to organize and manipulate data in a structured manner. However, modern matrices can involve billions of elements, making their storage and processing quite demanding in terms of computational resources and memory usage. Although prohibitively large, such matrices are often approximately low rank. We propose an algorithm that exploits this structure to obtain a low rank decomposition of any matrix $\mathbf{A}$ as $\mathbf{A} \approx \mathbf{L}\mathbf{R}$, where $\mathbf{L}$ and $\mathbf{R}$ are the low rank factors. The total number of elements in $\mathbf{L}$ and $\mathbf{R}$ can be significantly less than that in $\mathbf{A}$. Furthermore, the entries of $\mathbf{L}$ and $\mathbf{R}$ are quantized to low precision formats $--$ compressing $\mathbf{A}$ by giving us a low rank and low precision factorization. Our algorithm first computes an approximate basis of the range space of $\mathbf{A}$ by randomly sketching its columns, followed by a quantization of the vectors constituting this basis. It then computes approximate projections of the columns of $\mathbf{A}$ onto this quantized basis. We derive upper bounds on the approximation error of our algorithm, and analyze the impact of target rank and quantization bit-budget. The tradeoff between compression ratio and approximation accuracy allows for flexibility in choosing these parameters based on specific application requirements. We empirically demonstrate the efficacy of our algorithm in image compression, nearest neighbor classification of image and text embeddings, and compressing the layers of LlaMa-$7$b. Our results illustrate that we can achieve compression ratios as aggressive as one bit per matrix coordinate, all while surpassing or maintaining the performance of traditional compression techniques.

Adversarial Approximate Inference for Speech to Electroglottograph Conversion

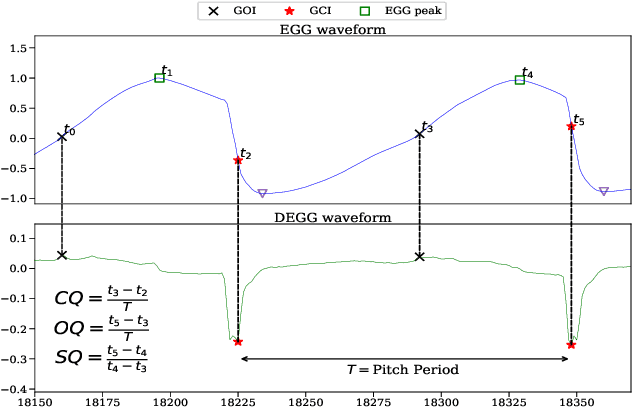
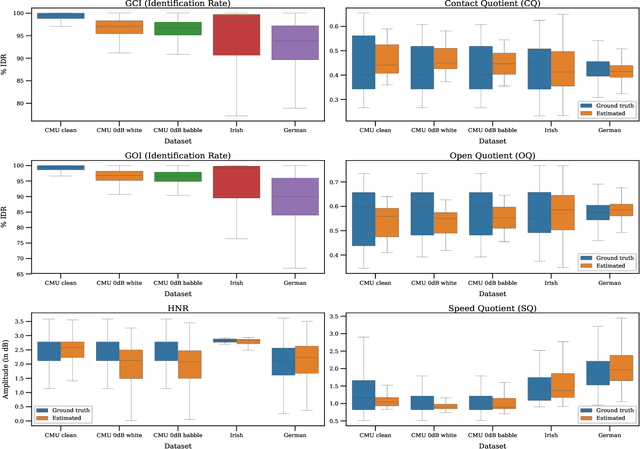
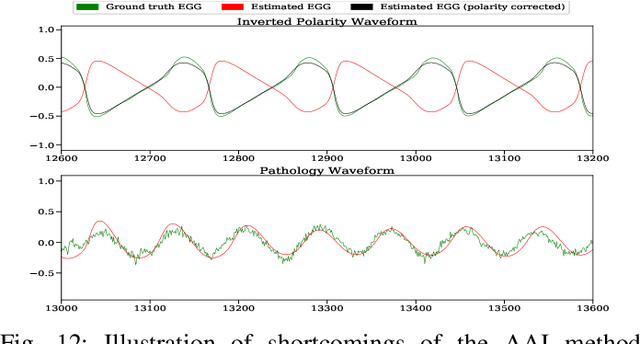
Speech produced by human vocal apparatus conveys substantial non-semantic information including the gender of the speaker, voice quality, affective state, abnormalities in the vocal apparatus etc. Such information is attributed to the properties of the voice source signal, which is usually estimated from the speech signal. However, most of the source estimation techniques depend heavily on the goodness of the model assumptions and are prone to noise. A popular alternative is to indirectly obtain the source information through the Electroglottographic (EGG) signal that measures the electrical admittance around the vocal folds using a dedicated hardware. In this paper, we address the problem of estimating the EGG signal directly from the speech signal, devoid of any hardware. Sampling from the intractable conditional distribution of the EGG signal given the speech signal is accomplished through optimization of an evidence lower bound. This is constructed via minimization of the KL-divergence between the true and the approximated posteriors of a latent variable learned using a deep neural auto-encoder that serves an informative prior which reconstructs the EGG signal. We demonstrate the efficacy of the method to generate EGG signal by conducting several experiments on datasets comprising multiple speakers, voice qualities, noise settings and speech pathologies. The proposed method is evaluated on many benchmark metrics and is found to agree with the gold standards while being better than the state-of-the-art algorithms on a few tasks such as epoch extraction.