Matrix Compression via Randomized Low Rank and Low Precision Factorization
Paper and Code
Oct 17, 2023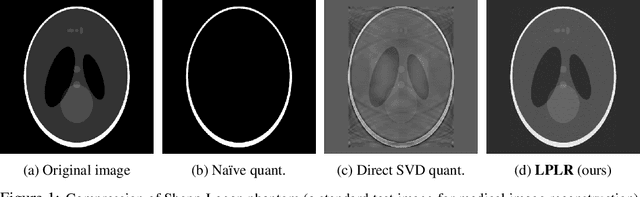


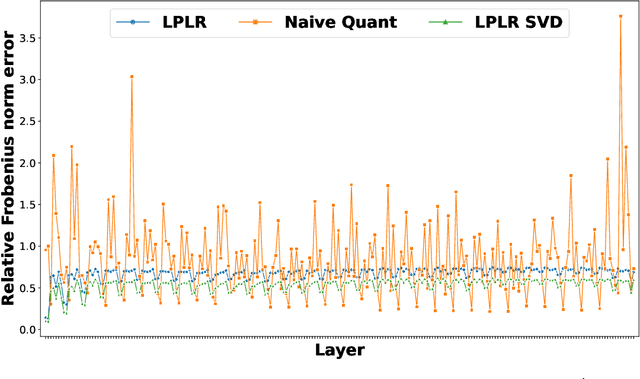
Matrices are exceptionally useful in various fields of study as they provide a convenient framework to organize and manipulate data in a structured manner. However, modern matrices can involve billions of elements, making their storage and processing quite demanding in terms of computational resources and memory usage. Although prohibitively large, such matrices are often approximately low rank. We propose an algorithm that exploits this structure to obtain a low rank decomposition of any matrix $\mathbf{A}$ as $\mathbf{A} \approx \mathbf{L}\mathbf{R}$, where $\mathbf{L}$ and $\mathbf{R}$ are the low rank factors. The total number of elements in $\mathbf{L}$ and $\mathbf{R}$ can be significantly less than that in $\mathbf{A}$. Furthermore, the entries of $\mathbf{L}$ and $\mathbf{R}$ are quantized to low precision formats $--$ compressing $\mathbf{A}$ by giving us a low rank and low precision factorization. Our algorithm first computes an approximate basis of the range space of $\mathbf{A}$ by randomly sketching its columns, followed by a quantization of the vectors constituting this basis. It then computes approximate projections of the columns of $\mathbf{A}$ onto this quantized basis. We derive upper bounds on the approximation error of our algorithm, and analyze the impact of target rank and quantization bit-budget. The tradeoff between compression ratio and approximation accuracy allows for flexibility in choosing these parameters based on specific application requirements. We empirically demonstrate the efficacy of our algorithm in image compression, nearest neighbor classification of image and text embeddings, and compressing the layers of LlaMa-$7$b. Our results illustrate that we can achieve compression ratios as aggressive as one bit per matrix coordinate, all while surpassing or maintaining the performance of traditional compression techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge