Game-Theoretic Joint Incentive and Cut Layer Selection Mechanism in Split Federated Learning

To alleviate the training burden in federated learning while enhancing convergence speed, Split Federated Learning (SFL) has emerged as a promising approach by combining the advantages of federated and split learning. However, recent studies have largely overlooked competitive situations. In this framework, the SFL model owner can choose the cut layer to balance the training load between the server and clients, ensuring the necessary level of privacy for the clients. Additionally, the SFL model owner sets incentives to encourage client participation in the SFL process. The optimization strategies employed by the SFL model owner influence clients' decisions regarding the amount of data they contribute, taking into account the shared incentives over clients and anticipated energy consumption during SFL. To address this framework, we model the problem using a hierarchical decision-making approach, formulated as a single-leader multi-follower Stackelberg game. We demonstrate the existence and uniqueness of the Nash equilibrium among clients and analyze the Stackelberg equilibrium by examining the leader's game. Furthermore, we discuss privacy concerns related to differential privacy and the criteria for selecting the minimum required cut layer. Our findings show that the Stackelberg equilibrium solution maximizes the utility for both the clients and the SFL model owner.

Collaborative Inference over Wireless Channels with Feature Differential Privacy

Collaborative inference among multiple wireless edge devices has the potential to significantly enhance Artificial Intelligence (AI) applications, particularly for sensing and computer vision. This approach typically involves a three-stage process: a) data acquisition through sensing, b) feature extraction, and c) feature encoding for transmission. However, transmitting the extracted features poses a significant privacy risk, as sensitive personal data can be exposed during the process. To address this challenge, we propose a novel privacy-preserving collaborative inference mechanism, wherein each edge device in the network secures the privacy of extracted features before transmitting them to a central server for inference. Our approach is designed to achieve two primary objectives: 1) reducing communication overhead and 2) ensuring strict privacy guarantees during feature transmission, while maintaining effective inference performance. Additionally, we introduce an over-the-air pooling scheme specifically designed for classification tasks, which provides formal guarantees on the privacy of transmitted features and establishes a lower bound on classification accuracy.

Privacy Preserving Semi-Decentralized Mean Estimation over Intermittently-Connected Networks

We consider the problem of privately estimating the mean of vectors distributed across different nodes of an unreliable wireless network, where communications between nodes can fail intermittently. We adopt a semi-decentralized setup, wherein to mitigate the impact of intermittently connected links, nodes can collaborate with their neighbors to compute a local consensus, which they relay to a central server. In such a setting, the communications between any pair of nodes must ensure that the privacy of the nodes is rigorously maintained to prevent unauthorized information leakage. We study the tradeoff between collaborative relaying and privacy leakage due to the data sharing among nodes and, subsequently, propose PriCER: Private Collaborative Estimation via Relaying -- a differentially private collaborative algorithm for mean estimation to optimize this tradeoff. The privacy guarantees of PriCER arise (i) implicitly, by exploiting the inherent stochasticity of the flaky network connections, and (ii) explicitly, by adding Gaussian perturbations to the estimates exchanged by the nodes. Local and central privacy guarantees are provided against eavesdroppers who can observe different signals, such as the communications amongst nodes during local consensus and (possibly multiple) transmissions from the relays to the central server. We substantiate our theoretical findings with numerical simulations. Our implementation is available at https://github.com/rajarshisaha95/private-collaborative-relaying.

Clustering Mixtures of Discrete Distributions: A Note on Mitra's Algorithm

In this note, we provide a refined analysis of Mitra's algorithm \cite{mitra2008clustering} for classifying general discrete mixture distribution models. Built upon spectral clustering \cite{mcsherry2001spectral}, this algorithm offers compelling conditions for probability distributions. We enhance this analysis by tailoring the model to bipartite stochastic block models, resulting in more refined conditions. Compared to those derived in \cite{mitra2008clustering}, our improved separation conditions are obtained.

Exploring the Privacy-Energy Consumption Tradeoff for Split Federated Learning

Split Federated Learning (SFL) has recently emerged as a promising distributed learning technology, leveraging the strengths of both federated learning and split learning. It emphasizes the advantages of rapid convergence while addressing privacy concerns. As a result, this innovation has received significant attention from both industry and academia. However, since the model is split at a specific layer, known as a cut layer, into both client-side and server-side models for the SFL, the choice of the cut layer in SFL can have a substantial impact on the energy consumption of clients and their privacy, as it influences the training burden and the output of the client-side models. Moreover, the design challenge of determining the cut layer is highly intricate, primarily due to the inherent heterogeneity in the computing and networking capabilities of clients. In this article, we provide a comprehensive overview of the SFL process and conduct a thorough analysis of energy consumption and privacy. This analysis takes into account the influence of various system parameters on the cut layer selection strategy. Additionally, we provide an illustrative example of the cut layer selection, aiming to minimize the risk of clients from reconstructing the raw data at the server while sustaining energy consumption within the required energy budget, which involve trade-offs. Finally, we address open challenges in this field including their applications to 6G technology. These directions represent promising avenues for future research and development.

Collaborative Mean Estimation over Intermittently Connected Networks with Peer-To-Peer Privacy

This work considers the problem of Distributed Mean Estimation (DME) over networks with intermittent connectivity, where the goal is to learn a global statistic over the data samples localized across distributed nodes with the help of a central server. To mitigate the impact of intermittent links, nodes can collaborate with their neighbors to compute local consensus which they forward to the central server. In such a setup, the communications between any pair of nodes must satisfy local differential privacy constraints. We study the tradeoff between collaborative relaying and privacy leakage due to the additional data sharing among nodes and, subsequently, propose a novel differentially private collaborative algorithm for DME to achieve the optimal tradeoff. Finally, we present numerical simulations to substantiate our theoretical findings.

Differentially Private Community Detection for Stochastic Block Models

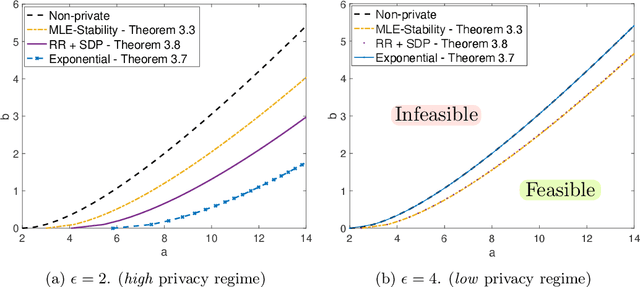
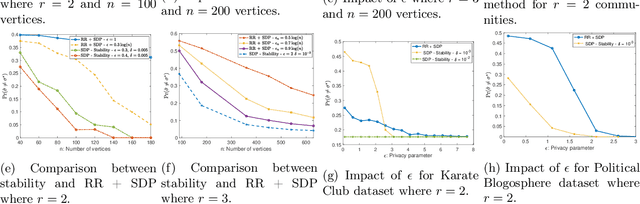
The goal of community detection over graphs is to recover underlying labels/attributes of users (e.g., political affiliation) given the connectivity between users (represented by adjacency matrix of a graph). There has been significant recent progress on understanding the fundamental limits of community detection when the graph is generated from a stochastic block model (SBM). Specifically, sharp information theoretic limits and efficient algorithms have been obtained for SBMs as a function of $p$ and $q$, which represent the intra-community and inter-community connection probabilities. In this paper, we study the community detection problem while preserving the privacy of the individual connections (edges) between the vertices. Focusing on the notion of $(\epsilon, \delta)$-edge differential privacy (DP), we seek to understand the fundamental tradeoffs between $(p, q)$, DP budget $(\epsilon, \delta)$, and computational efficiency for exact recovery of the community labels. To this end, we present and analyze the associated information-theoretic tradeoffs for three broad classes of differentially private community recovery mechanisms: a) stability based mechanism; b) sampling based mechanisms; and c) graph perturbation mechanisms. Our main findings are that stability and sampling based mechanisms lead to a superior tradeoff between $(p,q)$ and the privacy budget $(\epsilon, \delta)$; however this comes at the expense of higher computational complexity. On the other hand, albeit low complexity, graph perturbation mechanisms require the privacy budget $\epsilon$ to scale as $\Omega(\log(n))$ for exact recovery. To the best of our knowledge, this is the first work to study the impact of privacy constraints on the fundamental limits for community detection.

Privacy Amplification for Federated Learning via User Sampling and Wireless Aggregation

In this paper, we study the problem of federated learning over a wireless channel with user sampling, modeled by a Gaussian multiple access channel, subject to central and local differential privacy (DP/LDP) constraints. It has been shown that the superposition nature of the wireless channel provides a dual benefit of bandwidth efficient gradient aggregation, in conjunction with strong DP guarantees for the users. Specifically, the central DP privacy leakage has been shown to scale as $\mathcal{O}(1/K^{1/2})$, where $K$ is the number of users. It has also been shown that user sampling coupled with orthogonal transmission can enhance the central DP privacy leakage with the same scaling behavior. In this work, we show that, by join incorporating both wireless aggregation and user sampling, one can obtain even stronger privacy guarantees. We propose a private wireless gradient aggregation scheme, which relies on independently randomized participation decisions by each user. The central DP leakage of our proposed scheme scales as $\mathcal{O}(1/K^{3/4})$. In addition, we show that LDP is also boosted by user sampling. We also present analysis for the convergence rate of the proposed scheme and study the tradeoffs between wireless resources, convergence, and privacy theoretically and empirically for two scenarios when the number of sampled participants are $(a)$ known, or $(b)$ unknown at the parameter server.