Differentially Private Community Detection for Stochastic Block Models
Paper and Code
Jan 31, 2022
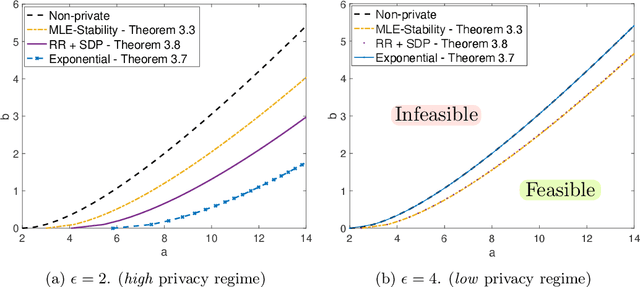
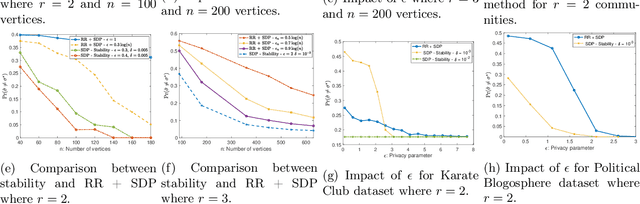

The goal of community detection over graphs is to recover underlying labels/attributes of users (e.g., political affiliation) given the connectivity between users (represented by adjacency matrix of a graph). There has been significant recent progress on understanding the fundamental limits of community detection when the graph is generated from a stochastic block model (SBM). Specifically, sharp information theoretic limits and efficient algorithms have been obtained for SBMs as a function of $p$ and $q$, which represent the intra-community and inter-community connection probabilities. In this paper, we study the community detection problem while preserving the privacy of the individual connections (edges) between the vertices. Focusing on the notion of $(\epsilon, \delta)$-edge differential privacy (DP), we seek to understand the fundamental tradeoffs between $(p, q)$, DP budget $(\epsilon, \delta)$, and computational efficiency for exact recovery of the community labels. To this end, we present and analyze the associated information-theoretic tradeoffs for three broad classes of differentially private community recovery mechanisms: a) stability based mechanism; b) sampling based mechanisms; and c) graph perturbation mechanisms. Our main findings are that stability and sampling based mechanisms lead to a superior tradeoff between $(p,q)$ and the privacy budget $(\epsilon, \delta)$; however this comes at the expense of higher computational complexity. On the other hand, albeit low complexity, graph perturbation mechanisms require the privacy budget $\epsilon$ to scale as $\Omega(\log(n))$ for exact recovery. To the best of our knowledge, this is the first work to study the impact of privacy constraints on the fundamental limits for community detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge