Distributed Learning and Democratic Embeddings: Polynomial-Time Source Coding Schemes Can Achieve Minimax Lower Bounds for Distributed Gradient Descent under Communication Constraints
Paper and Code
Mar 13, 2021
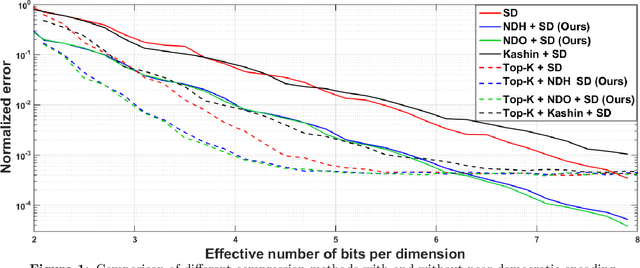
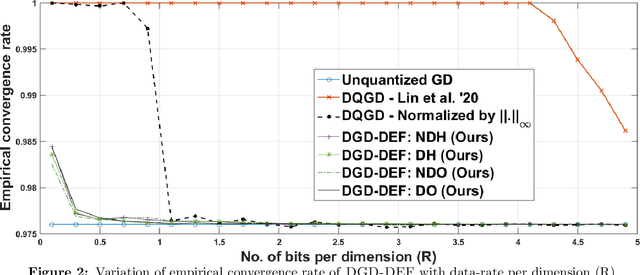
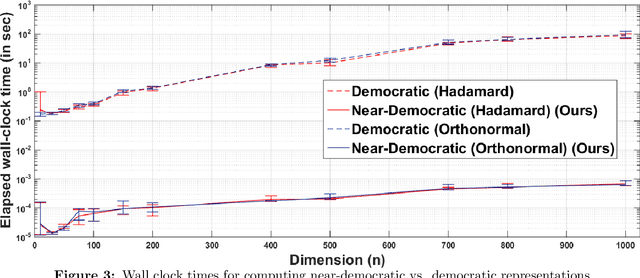
In this work, we consider the distributed optimization setting where information exchange between the computation nodes and the parameter server is subject to a maximum bit-budget. We first consider the problem of compressing a vector in the n-dimensional Euclidean space, subject to a bit-budget of R-bits per dimension, for which we introduce Democratic and Near-Democratic source-coding schemes. We show that these coding schemes are (near) optimal in the sense that the covering efficiency of the resulting quantizer is either dimension independent, or has a very weak logarithmic dependence. Subsequently, we propose a distributed optimization algorithm: DGD-DEF, which employs our proposed coding strategy, and achieves the minimax optimal convergence rate to within (near) constant factors for a class of communication-constrained distributed optimization algorithms. Furthermore, we extend the utility of our proposed source coding scheme by showing that it can remarkably improve the performance when used in conjunction with other compression schemes. We validate our theoretical claims through numerical simulations. Keywords: Fast democratic (Kashin) embeddings, Distributed optimization, Data-rate constraint, Quantized gradient descent, Error feedback.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge