Minimax Optimal Quantization of Linear Models: Information-Theoretic Limits and Efficient Algorithms
Paper and Code
Feb 23, 2022
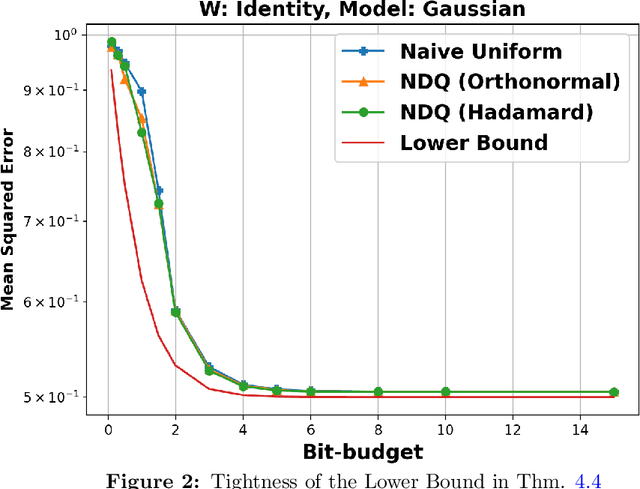
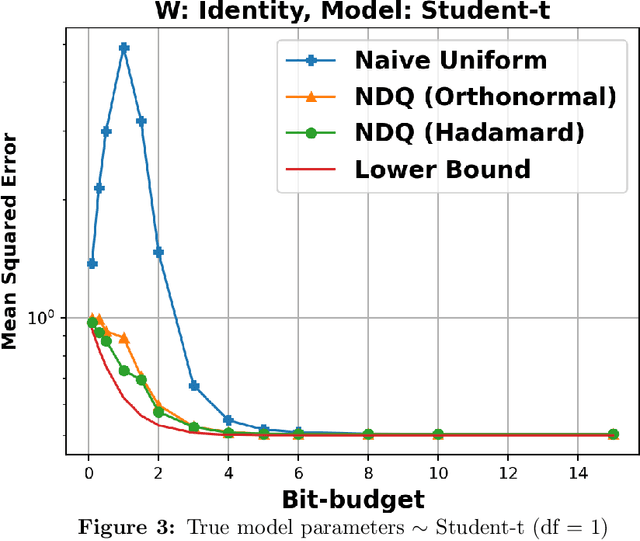
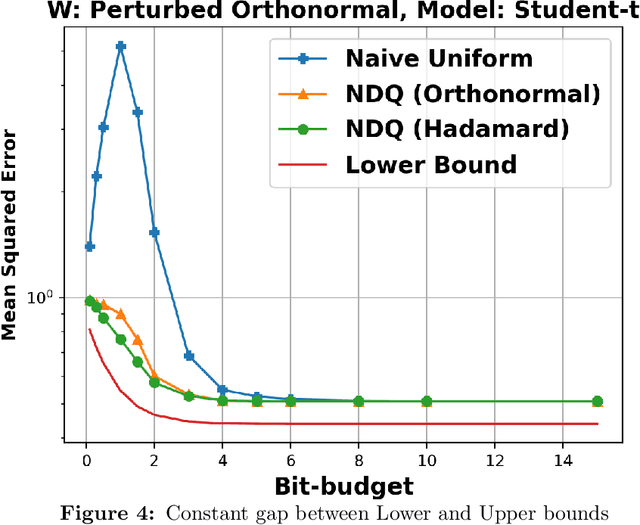
We consider the problem of quantizing a linear model learned from measurements $\mathbf{X} = \mathbf{W}\boldsymbol{\theta} + \mathbf{v}$. The model is constrained to be representable using only $dB$-bits, where $B \in (0, \infty)$ is a pre-specified budget and $d$ is the dimension of the model. We derive an information-theoretic lower bound for the minimax risk under this setting and show that it is tight with a matching upper bound. This upper bound is achieved using randomized embedding based algorithms. We propose randomized Hadamard embeddings that are computationally efficient while performing near-optimally. We also show that our method and upper-bounds can be extended for two-layer ReLU neural networks. Numerical simulations validate our theoretical claims.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge