NeuRes: Learning Proofs of Propositional Satisfiability

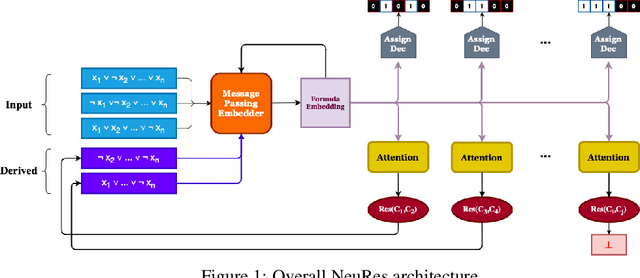
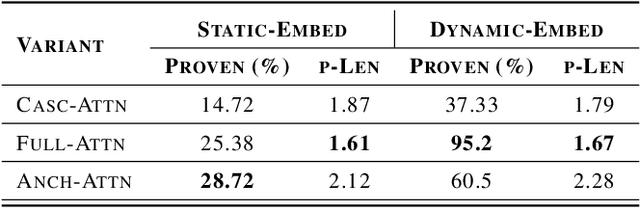
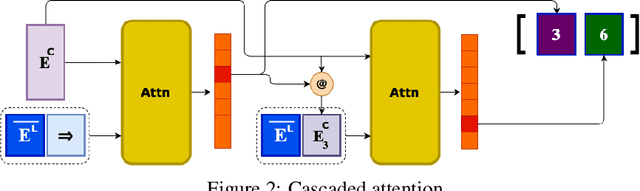
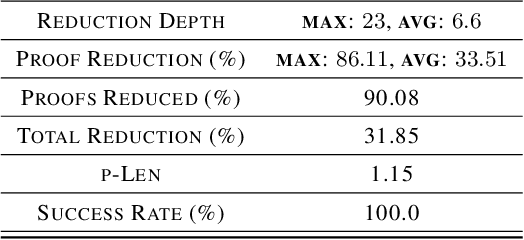
We introduce NeuRes, a neuro-symbolic proof-based SAT solver. Unlike other neural SAT solving methods, NeuRes is capable of proving unsatisfiability as opposed to merely predicting it. By design, NeuRes operates in a certificate-driven fashion by employing propositional resolution to prove unsatisfiability and to accelerate the process of finding satisfying truth assignments in case of unsat and sat formulas, respectively. To realize this, we propose a novel architecture that adapts elements from Graph Neural Networks and Pointer Networks to autoregressively select pairs of nodes from a dynamic graph structure, which is essential to the generation of resolution proofs. Our model is trained and evaluated on a dataset of teacher proofs and truth assignments that we compiled with the same random formula distribution used by NeuroSAT. In our experiments, we show that NeuRes solves more test formulas than NeuroSAT by a rather wide margin on different distributions while being much more data-efficient. Furthermore, we show that NeuRes is capable of largely shortening teacher proofs by notable proportions. We use this feature to devise a bootstrapped training procedure that manages to reduce a dataset of proofs generated by an advanced solver by ~23% after training on it with no extra guidance.

Breaking the De-Pois Poisoning Defense

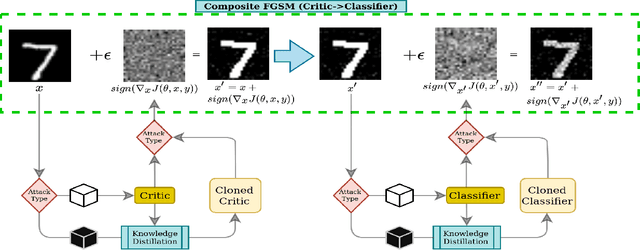
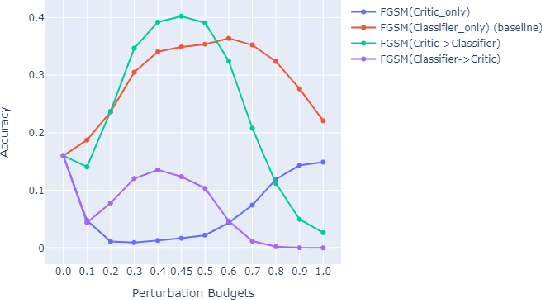
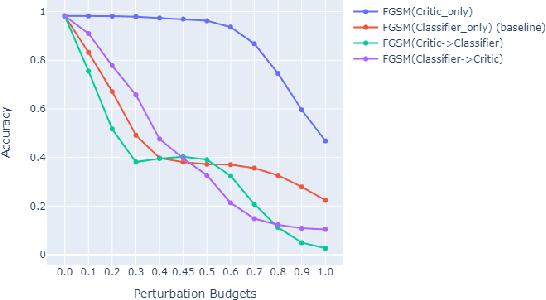
Attacks on machine learning models have been, since their conception, a very persistent and evasive issue resembling an endless cat-and-mouse game. One major variant of such attacks is poisoning attacks which can indirectly manipulate an ML model. It has been observed over the years that the majority of proposed effective defense models are only effective when an attacker is not aware of them being employed. In this paper, we show that the attack-agnostic De-Pois defense is hardly an exception to that rule. In fact, we demonstrate its vulnerability to the simplest White-Box and Black-Box attacks by an attacker that knows the structure of the De-Pois defense model. In essence, the De-Pois defense relies on a critic model that can be used to detect poisoned data before passing it to the target model. In our work, we break this poison-protection layer by replicating the critic model and then performing a composed gradient-sign attack on both the critic and target models simultaneously -- allowing us to bypass the critic firewall to poison the target model.

FLoBC: A Decentralized Blockchain-Based Federated Learning Framework

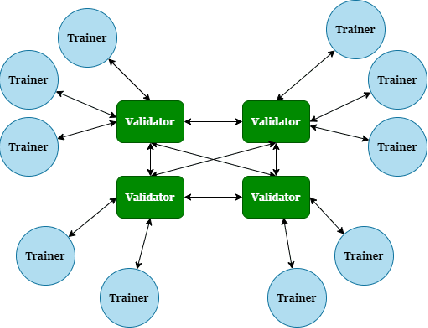
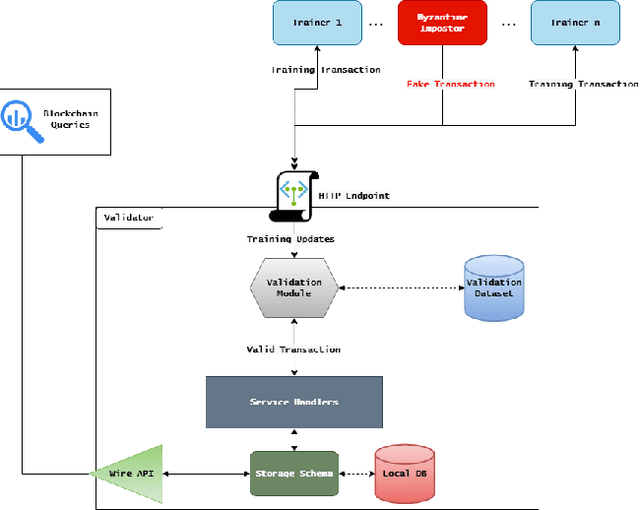
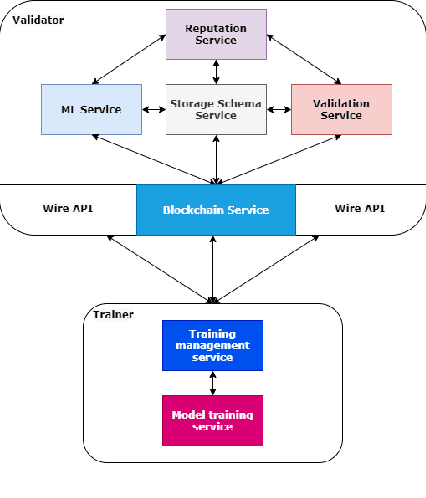
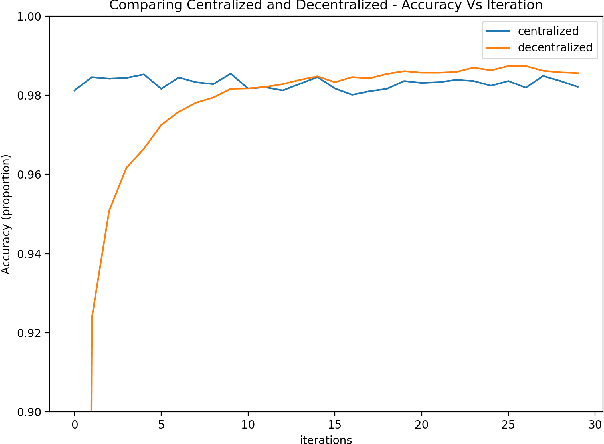
The rapid expansion of data worldwide invites the need for more distributed solutions in order to apply machine learning on a much wider scale. The resultant distributed learning systems can have various degrees of centralization. In this work, we demonstrate our solution FLoBC for building a generic decentralized federated learning system using blockchain technology, accommodating any machine learning model that is compatible with gradient descent optimization. We present our system design comprising the two decentralized actors: trainer and validator, alongside our methodology for ensuring reliable and efficient operation of said system. Finally, we utilize FLoBC as an experimental sandbox to compare and contrast the effects of trainer-to-validator ratio, reward-penalty policy, and model synchronization schemes on the overall system performance, ultimately showing by example that a decentralized federated learning system is indeed a feasible alternative to more centralized architectures.

On Theoretical Complexity and Boolean Satisfiability

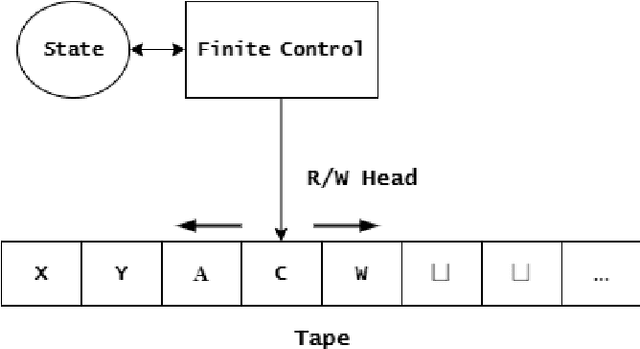
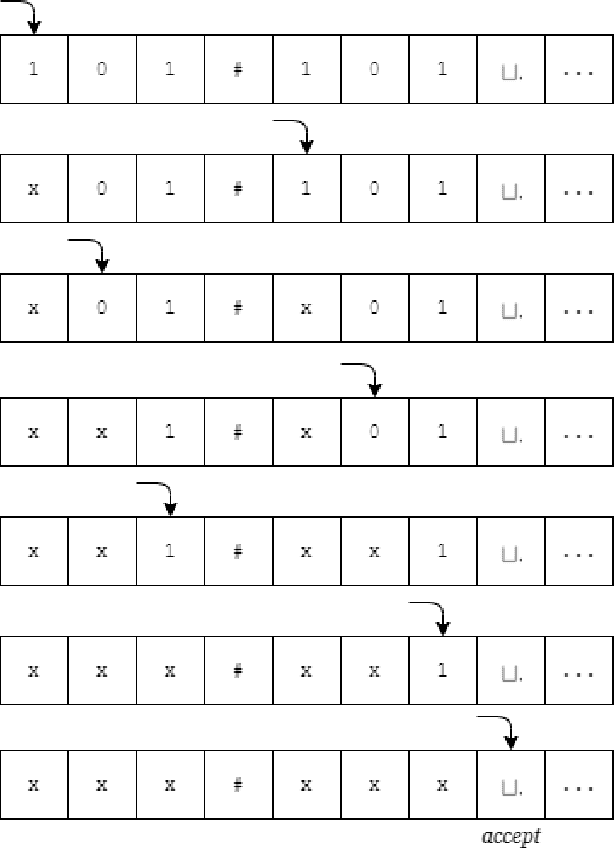
Theoretical complexity is a vital subfield of computer science that enables us to mathematically investigate computation and answer many interesting queries about the nature of computational problems. It provides theoretical tools to assess time and space requirements of computations along with assessing the difficultly of problems - classifying them accordingly. It also garners at its core one of the most important problems in mathematics, namely, the $\textbf{P vs. NP}$ millennium problem. In essence, this problem asks whether solution and verification reside on two different levels of difficulty. In this thesis, we introduce some of the most central concepts in the Theory of Computing, giving an overview of how computation can be abstracted using Turing machines. Further, we introduce the two most famous problem complexity classes $\textbf{P}$ and $\textbf{NP}$ along with the relationship between them. In addition, we explicate the concept of problem reduction and how it is an essential tool for making hardness comparisons between different problems. Later, we present the problem of Boolean Satisfiability (SAT) which lies at the center of NP-complete problems. We then explore some of its tractable as well as intractable variants such as Horn-SAT and 3-SAT, respectively. Last but not least, we establish polynomial-time reductions from 3-SAT to some of the famous NP-complete graph problems, namely, Clique Finding, Hamiltonian Cycle Finding, and 3-Coloring.