On Theoretical Complexity and Boolean Satisfiability
Paper and Code
Dec 22, 2021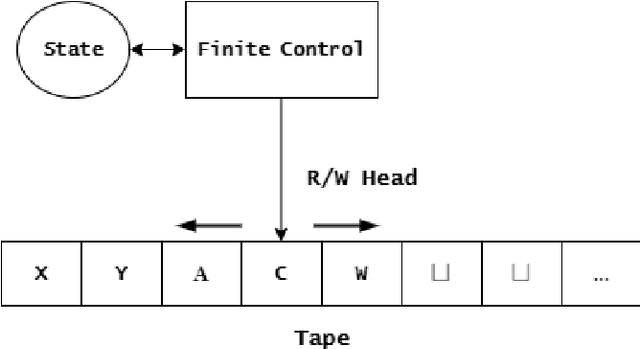

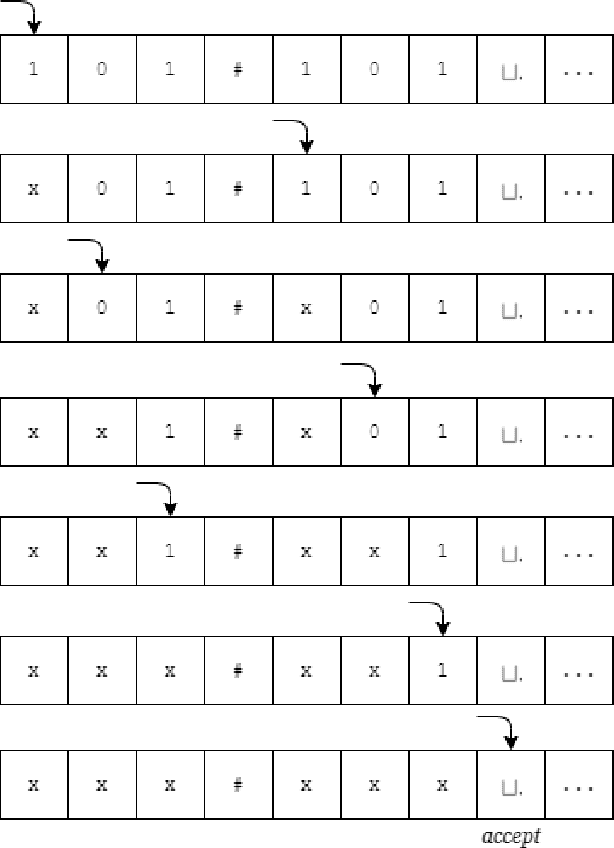

Theoretical complexity is a vital subfield of computer science that enables us to mathematically investigate computation and answer many interesting queries about the nature of computational problems. It provides theoretical tools to assess time and space requirements of computations along with assessing the difficultly of problems - classifying them accordingly. It also garners at its core one of the most important problems in mathematics, namely, the $\textbf{P vs. NP}$ millennium problem. In essence, this problem asks whether solution and verification reside on two different levels of difficulty. In this thesis, we introduce some of the most central concepts in the Theory of Computing, giving an overview of how computation can be abstracted using Turing machines. Further, we introduce the two most famous problem complexity classes $\textbf{P}$ and $\textbf{NP}$ along with the relationship between them. In addition, we explicate the concept of problem reduction and how it is an essential tool for making hardness comparisons between different problems. Later, we present the problem of Boolean Satisfiability (SAT) which lies at the center of NP-complete problems. We then explore some of its tractable as well as intractable variants such as Horn-SAT and 3-SAT, respectively. Last but not least, we establish polynomial-time reductions from 3-SAT to some of the famous NP-complete graph problems, namely, Clique Finding, Hamiltonian Cycle Finding, and 3-Coloring.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge