Aligning Language Models for Versatile Text-based Item Retrieval

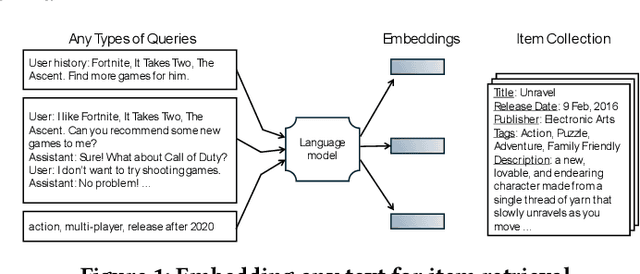
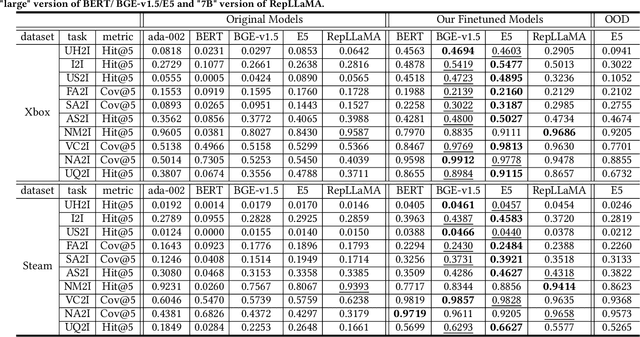
This paper addresses the gap between general-purpose text embeddings and the specific demands of item retrieval tasks. We demonstrate the shortcomings of existing models in capturing the nuances necessary for zero-shot performance on item retrieval tasks. To overcome these limitations, we propose generate in-domain dataset from ten tasks tailored to unlocking models' representation ability for item retrieval. Our empirical studies demonstrate that fine-tuning embedding models on the dataset leads to remarkable improvements in a variety of retrieval tasks. We also illustrate the practical application of our refined model in a conversational setting, where it enhances the capabilities of LLM-based Recommender Agents like Chat-Rec. Our code is available at https://github.com/microsoft/RecAI.

Ensemble linear interpolators: The role of ensembling

Interpolators are unstable. For example, the mininum $\ell_2$ norm least square interpolator exhibits unbounded test errors when dealing with noisy data. In this paper, we study how ensemble stabilizes and thus improves the generalization performance, measured by the out-of-sample prediction risk, of an individual interpolator. We focus on bagged linear interpolators, as bagging is a popular randomization-based ensemble method that can be implemented in parallel. We introduce the multiplier-bootstrap-based bagged least square estimator, which can then be formulated as an average of the sketched least square estimators. The proposed multiplier bootstrap encompasses the classical bootstrap with replacement as a special case, along with a more intriguing variant which we call the Bernoulli bootstrap. Focusing on the proportional regime where the sample size scales proportionally with the feature dimensionality, we investigate the out-of-sample prediction risks of the sketched and bagged least square estimators in both underparametrized and overparameterized regimes. Our results reveal the statistical roles of sketching and bagging. In particular, sketching modifies the aspect ratio and shifts the interpolation threshold of the minimum $\ell_2$ norm estimator. However, the risk of the sketched estimator continues to be unbounded around the interpolation threshold due to excessive variance. In stark contrast, bagging effectively mitigates this variance, leading to a bounded limiting out-of-sample prediction risk. To further understand this stability improvement property, we establish that bagging acts as a form of implicit regularization, substantiated by the equivalence of the bagged estimator with its explicitly regularized counterpart. We also discuss several extensions.

ConvFormer: Revisiting Transformer for Sequential User Modeling

Sequential user modeling, a critical task in personalized recommender systems, focuses on predicting the next item a user would prefer, requiring a deep understanding of user behavior sequences. Despite the remarkable success of Transformer-based models across various domains, their full potential in comprehending user behavior remains untapped. In this paper, we re-examine Transformer-like architectures aiming to advance state-of-the-art performance. We start by revisiting the core building blocks of Transformer-based methods, analyzing the effectiveness of the item-to-item mechanism within the context of sequential user modeling. After conducting a thorough experimental analysis, we identify three essential criteria for devising efficient sequential user models, which we hope will serve as practical guidelines to inspire and shape future designs. Following this, we introduce ConvFormer, a simple but powerful modification to the Transformer architecture that meets these criteria, yielding state-of-the-art results. Additionally, we present an acceleration technique to minimize the complexity associated with processing extremely long sequences. Experiments on four public datasets showcase ConvFormer's superiority and confirm the validity of our proposed criteria.

Towards Explainable Collaborative Filtering with Taste Clusters Learning

Collaborative Filtering (CF) is a widely used and effective technique for recommender systems. In recent decades, there have been significant advancements in latent embedding-based CF methods for improved accuracy, such as matrix factorization, neural collaborative filtering, and LightGCN. However, the explainability of these models has not been fully explored. Adding explainability to recommendation models can not only increase trust in the decisionmaking process, but also have multiple benefits such as providing persuasive explanations for item recommendations, creating explicit profiles for users and items, and assisting item producers in design improvements. In this paper, we propose a neat and effective Explainable Collaborative Filtering (ECF) model that leverages interpretable cluster learning to achieve the two most demanding objectives: (1) Precise - the model should not compromise accuracy in the pursuit of explainability; and (2) Self-explainable - the model's explanations should truly reflect its decision-making process, not generated from post-hoc methods. The core of ECF is mining taste clusters from user-item interactions and item profiles.We map each user and item to a sparse set of taste clusters, and taste clusters are distinguished by a few representative tags. The user-item preference, users/items' cluster affiliations, and the generation of taste clusters are jointly optimized in an end-to-end manner. Additionally, we introduce a forest mechanism to ensure the model's accuracy, explainability, and diversity. To comprehensively evaluate the explainability quality of taste clusters, we design several quantitative metrics, including in-cluster item coverage, tag utilization, silhouette, and informativeness. Our model's effectiveness is demonstrated through extensive experiments on three real-world datasets.

How rotational invariance of common kernels prevents generalization in high dimensions

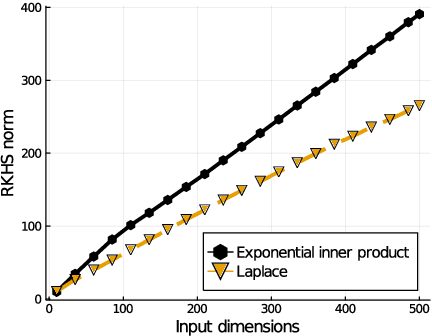
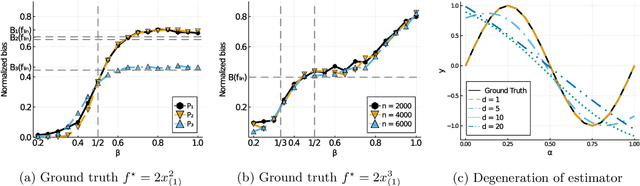
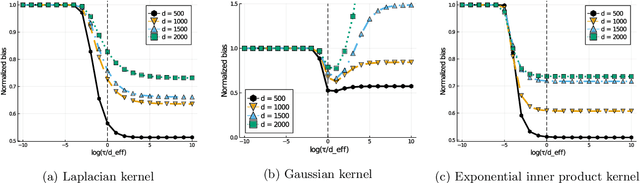
Kernel ridge regression is well-known to achieve minimax optimal rates in low-dimensional settings. However, its behavior in high dimensions is much less understood. Recent work establishes consistency for kernel regression under certain assumptions on the ground truth function and the distribution of the input data. In this paper, we show that the rotational invariance property of commonly studied kernels (such as RBF, inner product kernels and fully-connected NTK of any depth) induces a bias towards low-degree polynomials in high dimensions. Our result implies a lower bound on the generalization error for a wide range of distributions and various choices of the scaling for kernels with different eigenvalue decays. This lower bound suggests that general consistency results for kernel ridge regression in high dimensions require a more refined analysis that depends on the structure of the kernel beyond its eigenvalue decay.