ConFIG: Towards Conflict-free Training of Physics Informed Neural Networks

The loss functions of many learning problems contain multiple additive terms that can disagree and yield conflicting update directions. For Physics-Informed Neural Networks (PINNs), loss terms on initial/boundary conditions and physics equations are particularly interesting as they are well-established as highly difficult tasks. To improve learning the challenging multi-objective task posed by PINNs, we propose the ConFIG method, which provides conflict-free updates by ensuring a positive dot product between the final update and each loss-specific gradient. It also maintains consistent optimization rates for all loss terms and dynamically adjusts gradient magnitudes based on conflict levels. We additionally leverage momentum to accelerate optimizations by alternating the back-propagation of different loss terms. The proposed method is evaluated across a range of challenging PINN scenarios, consistently showing superior performance and runtime compared to baseline methods. We also test the proposed method in a classic multi-task benchmark, where the ConFIG method likewise exhibits a highly promising performance. Source code is available at \url{https://tum-pbs.github.io/ConFIG}.

Physics-Informed Learning of Characteristic Trajectories for Smoke Reconstruction

We delve into the physics-informed neural reconstruction of smoke and obstacles through sparse-view RGB videos, tackling challenges arising from limited observation of complex dynamics. Existing physics-informed neural networks often emphasize short-term physics constraints, leaving the proper preservation of long-term conservation less explored. We introduce Neural Characteristic Trajectory Fields, a novel representation utilizing Eulerian neural fields to implicitly model Lagrangian fluid trajectories. This topology-free, auto-differentiable representation facilitates efficient flow map calculations between arbitrary frames as well as efficient velocity extraction via auto-differentiation. Consequently, it enables end-to-end supervision covering long-term conservation and short-term physics priors. Building on the representation, we propose physics-informed trajectory learning and integration into NeRF-based scene reconstruction. We enable advanced obstacle handling through self-supervised scene decomposition and seamless integrated boundary constraints. Our results showcase the ability to overcome challenges like occlusion uncertainty, density-color ambiguity, and static-dynamic entanglements. Code and sample tests are at \url{https://github.com/19reborn/PICT_smoke}.

Physics Informed Neural Fields for Smoke Reconstruction with Sparse Data

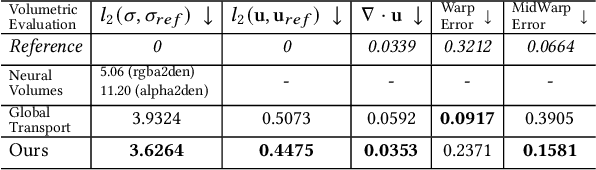
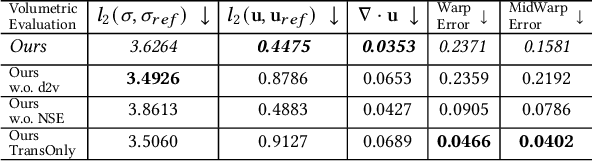
High-fidelity reconstruction of fluids from sparse multiview RGB videos remains a formidable challenge due to the complexity of the underlying physics as well as complex occlusion and lighting in captures. Existing solutions either assume knowledge of obstacles and lighting, or only focus on simple fluid scenes without obstacles or complex lighting, and thus are unsuitable for real-world scenes with unknown lighting or arbitrary obstacles. We present the first method to reconstruct dynamic fluid by leveraging the governing physics (ie, Navier -Stokes equations) in an end-to-end optimization from sparse videos without taking lighting conditions, geometry information, or boundary conditions as input. We provide a continuous spatio-temporal scene representation using neural networks as the ansatz of density and velocity solution functions for fluids as well as the radiance field for static objects. With a hybrid architecture that separates static and dynamic contents, fluid interactions with static obstacles are reconstructed for the first time without additional geometry input or human labeling. By augmenting time-varying neural radiance fields with physics-informed deep learning, our method benefits from the supervision of images and physical priors. To achieve robust optimization from sparse views, we introduced a layer-by-layer growing strategy to progressively increase the network capacity. Using progressively growing models with a new regularization term, we manage to disentangle density-color ambiguity in radiance fields without overfitting. A pretrained density-to-velocity fluid model is leveraged in addition as the data prior to avoid suboptimal velocity which underestimates vorticity but trivially fulfills physical equations. Our method exhibits high-quality results with relaxed constraints and strong flexibility on a representative set of synthetic and real flow captures.

Volumetric Isosurface Rendering with Deep Learning-Based Super-Resolution

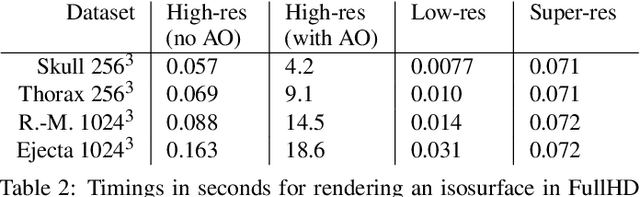
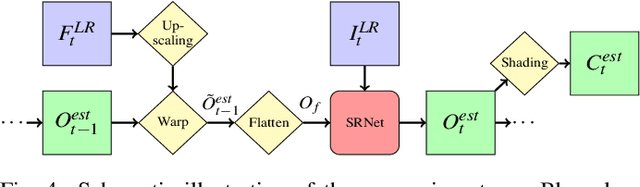
Rendering an accurate image of an isosurface in a volumetric field typically requires large numbers of data samples. Reducing the number of required samples lies at the core of research in volume rendering. With the advent of deep learning networks, a number of architectures have been proposed recently to infer missing samples in multi-dimensional fields, for applications such as image super-resolution and scan completion. In this paper, we investigate the use of such architectures for learning the upscaling of a low-resolution sampling of an isosurface to a higher resolution, with high fidelity reconstruction of spatial detail and shading. We introduce a fully convolutional neural network, to learn a latent representation generating a smooth, edge-aware normal field and ambient occlusions from a low-resolution normal and depth field. By adding a frame-to-frame motion loss into the learning stage, the upscaling can consider temporal variations and achieves improved frame-to-frame coherence. We demonstrate the quality of the network for isosurfaces which were never seen during training, and discuss remote and in-situ visualization as well as focus+context visualization as potential applications

A Multi-Pass GAN for Fluid Flow Super-Resolution

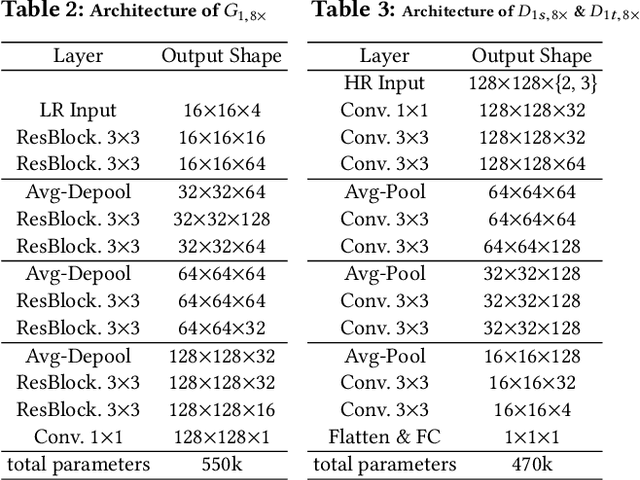
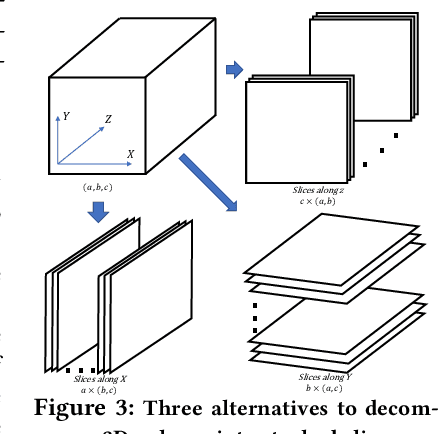
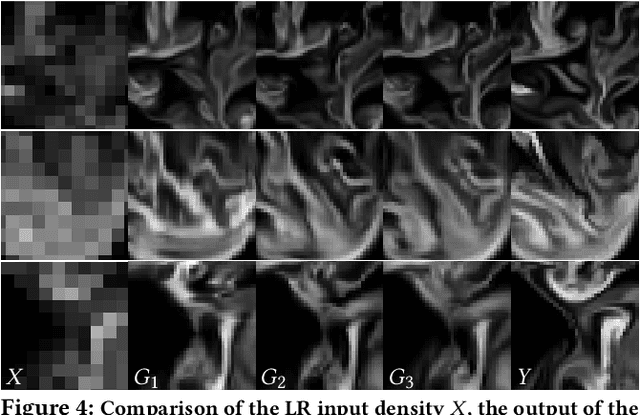
We propose a novel method to up-sample volumetric functions with generative neural networks using several orthogonal passes. Our method decomposes generative problems on Cartesian field functions into multiple smaller sub-problems that can be learned more efficiently. Specifically, we utilize two separate generative adversarial networks: the first one up-scales slices which are parallel to the XY-plane, whereas the second one refines the whole volume along the Z-axis working on slices in the YZ-plane. In this way, we obtain full coverage for the 3D target function and can leverage spatio-temporal supervision with a set of discriminators. Additionally, we demonstrate that our method can be combined with curriculum learning and progressive growing approaches. We arrive at a first method that can up-sample volumes by a factor of eight along each dimension, i.e., increasing the number of degrees of freedom by 512. Large volumetric up-scaling factors such as this one have previously not been attainable as the required number of weights in the neural networks renders adversarial training runs prohibitively difficult. We demonstrate the generality of our trained networks with a series of comparisons to previous work, a variety of complex 3D results, and an analysis of the resulting performance.

Temporally Coherent GANs for Video Super-Resolution (TecoGAN)

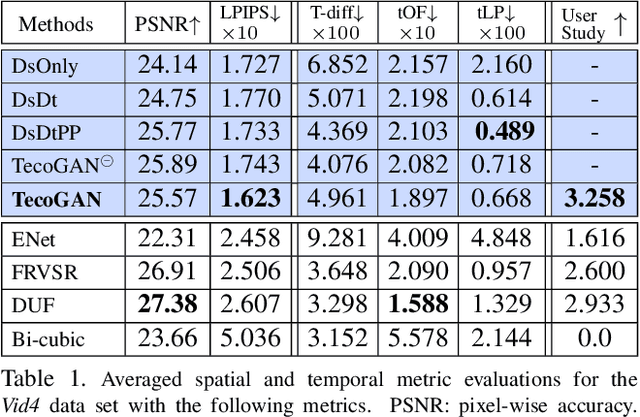
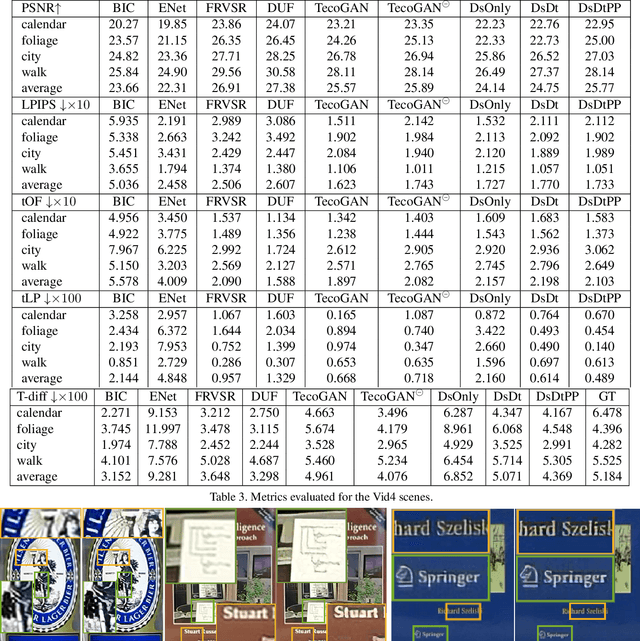
Adversarial training has been highly successful in the context of image super-resolution. It was demonstrated to yield realistic and highly detailed results. Despite this success, many state-of-the-art methods for video super-resolution still favor simpler norms such as $L_2$ over adversarial loss functions. This is caused by the fact that the averaging nature of direct vector norms as loss functions leads to temporal smoothness. The lack of spatial detail means temporal coherence is easily established. In our work, we instead propose an adversarial training for video super-resolution that leads to temporally coherent solutions without sacrificing spatial detail. In our generator, we use a recurrent, residual framework that naturally encourages temporal consistency. For adversarial training, we propose a novel spatio-temporal discriminator in combination with motion compensation to guarantee photo-realistic and temporally coherent details in the results. We additionally identify a class of temporal artifacts in these recurrent networks, and propose a novel Ping-Pong loss to remove them. Quantifying the temporal coherence for image super-resolution tasks has also not been addressed previously. We propose a first set of metrics to evaluate the accuracy as well as the perceptual quality of the temporal evolution, and we demonstrate that our method outperforms previous work by yielding realistic and detailed images with natural temporal changes.

tempoGAN: A Temporally Coherent, Volumetric GAN for Super-resolution Fluid Flow

We propose a temporally coherent generative model addressing the super-resolution problem for fluid flows. Our work represents a first approach to synthesize four-dimensional physics fields with neural networks. Based on a conditional generative adversarial network that is designed for the inference of three-dimensional volumetric data, our model generates consistent and detailed results by using a novel temporal discriminator, in addition to the commonly used spatial one. Our experiments show that the generator is able to infer more realistic high-resolution details by using additional physical quantities, such as low-resolution velocities or vorticities. Besides improvements in the training process and in the generated outputs, these inputs offer means for artistic control as well. We additionally employ a physics-aware data augmentation step, which is crucial to avoid overfitting and to reduce memory requirements. In this way, our network learns to generate advected quantities with highly detailed, realistic, and temporally coherent features. Our method works instantaneously, using only a single time-step of low-resolution fluid data. We demonstrate the abilities of our method using a variety of complex inputs and applications in two and three dimensions.

Data-Driven Synthesis of Smoke Flows with CNN-based Feature Descriptors

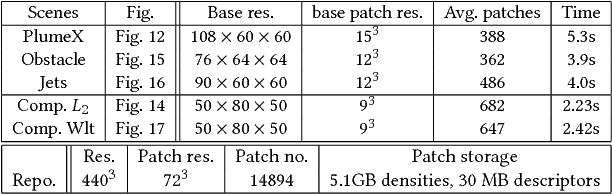
We present a novel data-driven algorithm to synthesize high-resolution flow simulations with reusable repositories of space-time flow data. In our work, we employ a descriptor learning approach to encode the similarity between fluid regions with differences in resolution and numerical viscosity. We use convolutional neural networks to generate the descriptors from fluid data such as smoke density and flow velocity. At the same time, we present a deformation limiting patch advection method which allows us to robustly track deformable fluid regions. With the help of this patch advection, we generate stable space-time data sets from detailed fluids for our repositories. We can then use our learned descriptors to quickly localize a suitable data set when running a new simulation. This makes our approach very efficient, and resolution independent. We will demonstrate with several examples that our method yields volumes with very high effective resolutions, and non-dissipative small scale details that naturally integrate into the motions of the underlying flow.