Maximilian Werhahn
A Multi-Pass GAN for Fluid Flow Super-Resolution
Jun 04, 2019
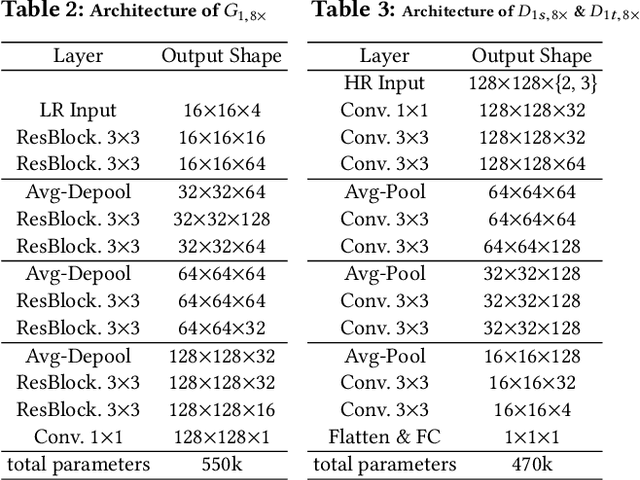
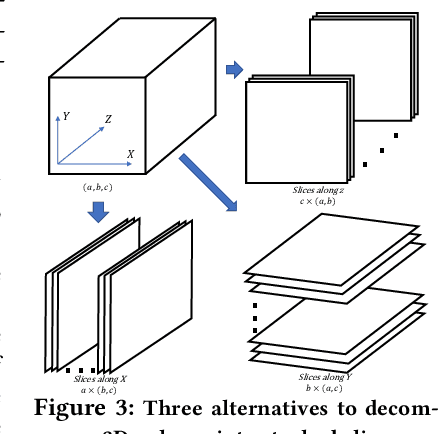
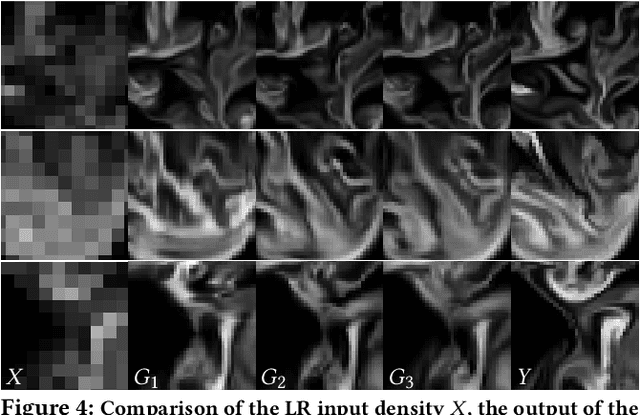
Abstract:We propose a novel method to up-sample volumetric functions with generative neural networks using several orthogonal passes. Our method decomposes generative problems on Cartesian field functions into multiple smaller sub-problems that can be learned more efficiently. Specifically, we utilize two separate generative adversarial networks: the first one up-scales slices which are parallel to the XY-plane, whereas the second one refines the whole volume along the Z-axis working on slices in the YZ-plane. In this way, we obtain full coverage for the 3D target function and can leverage spatio-temporal supervision with a set of discriminators. Additionally, we demonstrate that our method can be combined with curriculum learning and progressive growing approaches. We arrive at a first method that can up-sample volumes by a factor of eight along each dimension, i.e., increasing the number of degrees of freedom by 512. Large volumetric up-scaling factors such as this one have previously not been attainable as the required number of weights in the neural networks renders adversarial training runs prohibitively difficult. We demonstrate the generality of our trained networks with a series of comparisons to previous work, a variety of complex 3D results, and an analysis of the resulting performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge