Modeling and Analyzing Scorer Preferences in Short-Answer Math Questions

Automated scoring of student responses to open-ended questions, including short-answer questions, has great potential to scale to a large number of responses. Recent approaches for automated scoring rely on supervised learning, i.e., training classifiers or fine-tuning language models on a small number of responses with human-provided score labels. However, since scoring is a subjective process, these human scores are noisy and can be highly variable, depending on the scorer. In this paper, we investigate a collection of models that account for the individual preferences and tendencies of each human scorer in the automated scoring task. We apply these models to a short-answer math response dataset where each response is scored (often differently) by multiple different human scorers. We conduct quantitative experiments to show that our scorer models lead to improved automated scoring accuracy. We also conduct quantitative experiments and case studies to analyze the individual preferences and tendencies of scorers. We found that scorers can be grouped into several obvious clusters, with each cluster having distinct features, and analyzed them in detail.

Interpretable Math Word Problem Solution Generation Via Step-by-step Planning

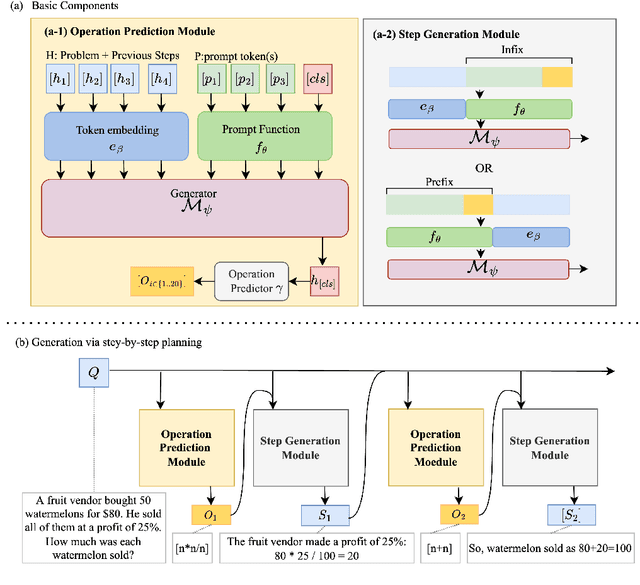
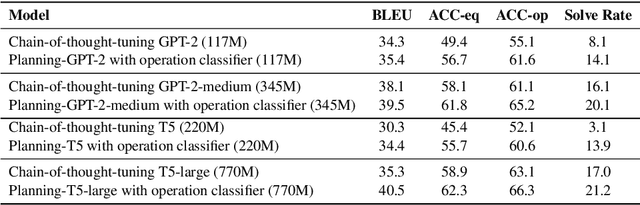
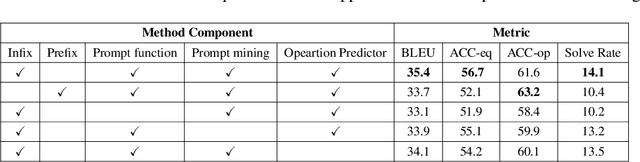
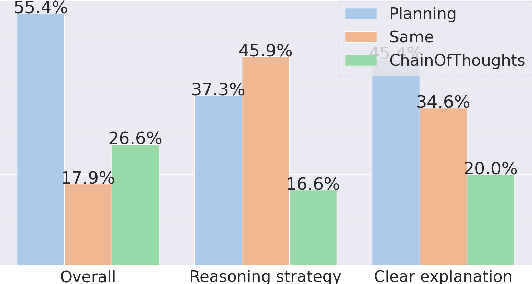
Solutions to math word problems (MWPs) with step-by-step explanations are valuable, especially in education, to help students better comprehend problem-solving strategies. Most existing approaches only focus on obtaining the final correct answer. A few recent approaches leverage intermediate solution steps to improve final answer correctness but often cannot generate coherent steps with a clear solution strategy. Contrary to existing work, we focus on improving the correctness and coherence of the intermediate solutions steps. We propose a step-by-step planning approach for intermediate solution generation, which strategically plans the generation of the next solution step based on the MWP and the previous solution steps. Our approach first plans the next step by predicting the necessary math operation needed to proceed, given history steps, then generates the next step, token-by-token, by prompting a language model with the predicted math operation. Experiments on the GSM8K dataset demonstrate that our approach improves the accuracy and interpretability of the solution on both automatic metrics and human evaluation.

Algebra Error Classification with Large Language Models

Automated feedback as students answer open-ended math questions has significant potential in improving learning outcomes at large scale. A key part of automated feedback systems is an error classification component, which identifies student errors and enables appropriate, predefined feedback to be deployed. Most existing approaches to error classification use a rule-based method, which has limited capacity to generalize. Existing data-driven methods avoid these limitations but specifically require mathematical expressions in student responses to be parsed into syntax trees. This requirement is itself a limitation, since student responses are not always syntactically valid and cannot be converted into trees. In this work, we introduce a flexible method for error classification using pre-trained large language models. We demonstrate that our method can outperform existing methods in algebra error classification, and is able to classify a larger set of student responses. Additionally, we analyze common classification errors made by our method and discuss limitations of automated error classification.

Automatic Short Math Answer Grading via In-context Meta-learning

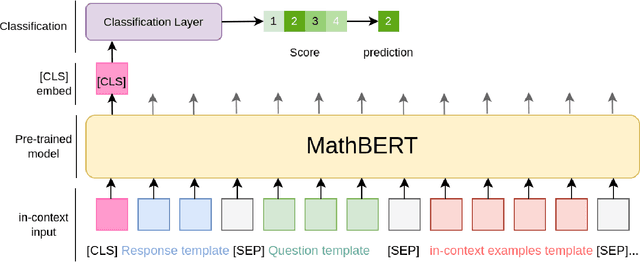
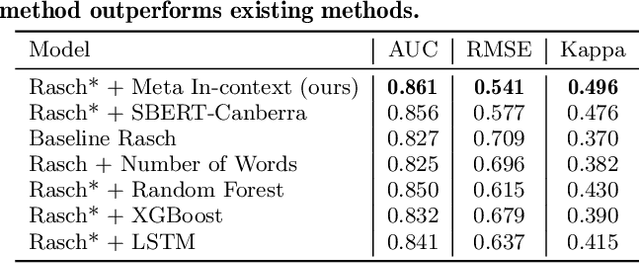
Automatic short answer grading is an important research direction in the exploration of how to use artificial intelligence (AI)-based tools to improve education. Current state-of-the-art approaches use neural language models to create vectorized representations of students responses, followed by classifiers to predict the score. However, these approaches have several key limitations, including i) they use pre-trained language models that are not well-adapted to educational subject domains and/or student-generated text and ii) they almost always train one model per question, ignoring the linkage across a question and result in a significant model storage problem due to the size of advanced language models. In this paper, we study the problem of automatic short answer grading for students' responses to math questions and propose a novel framework for this task. First, we use MathBERT, a variant of the popular language model BERT adapted to mathematical content, as our base model and fine-tune it for the downstream task of student response grading. Second, we use an in-context learning approach that provides scoring examples as input to the language model to provide additional context information and promote generalization to previously unseen questions. We evaluate our framework on a real-world dataset of student responses to open-ended math questions and show that our framework (often significantly) outperforms existing approaches, especially for new questions that are not seen during training.

Math Operation Embeddings for Open-ended Solution Analysis and Feedback

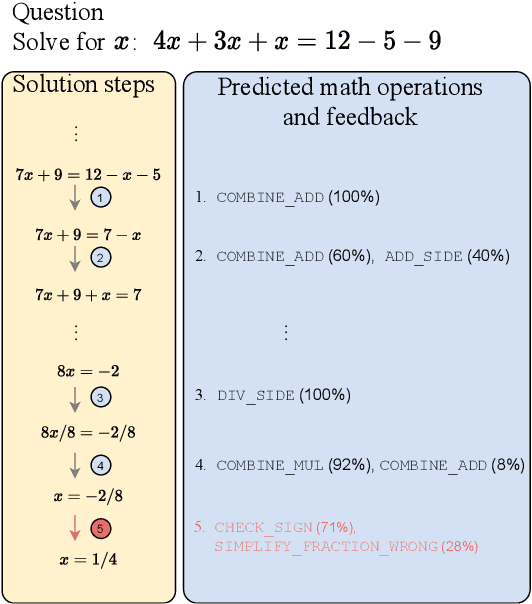
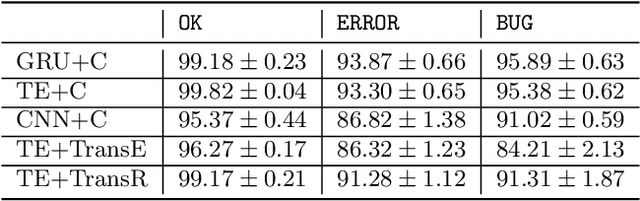
Feedback on student answers and even during intermediate steps in their solutions to open-ended questions is an important element in math education. Such feedback can help students correct their errors and ultimately lead to improved learning outcomes. Most existing approaches for automated student solution analysis and feedback require manually constructing cognitive models and anticipating student errors for each question. This process requires significant human effort and does not scale to most questions used in homework and practices that do not come with this information. In this paper, we analyze students' step-by-step solution processes to equation solving questions in an attempt to scale up error diagnostics and feedback mechanisms developed for a small number of questions to a much larger number of questions. Leveraging a recent math expression encoding method, we represent each math operation applied in solution steps as a transition in the math embedding vector space. We use a dataset that contains student solution steps in the Cognitive Tutor system to learn implicit and explicit representations of math operations. We explore whether these representations can i) identify math operations a student intends to perform in each solution step, regardless of whether they did it correctly or not, and ii) select the appropriate feedback type for incorrect steps. Experimental results show that our learned math operation representations generalize well across different data distributions.

Evaluating the Performance of Reinforcement Learning Algorithms

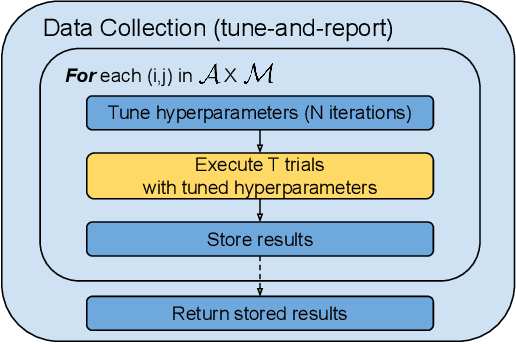
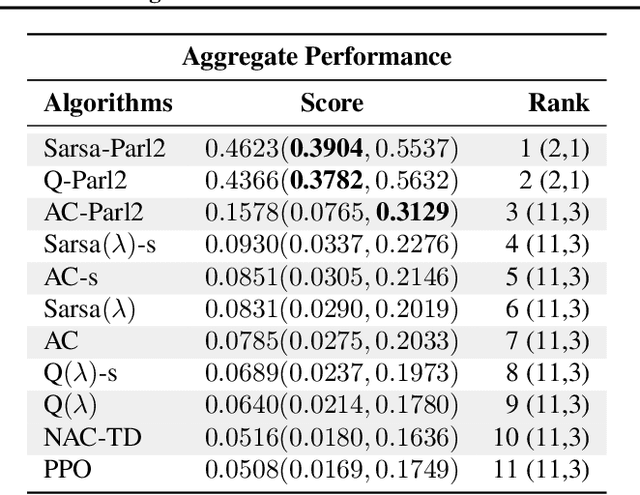
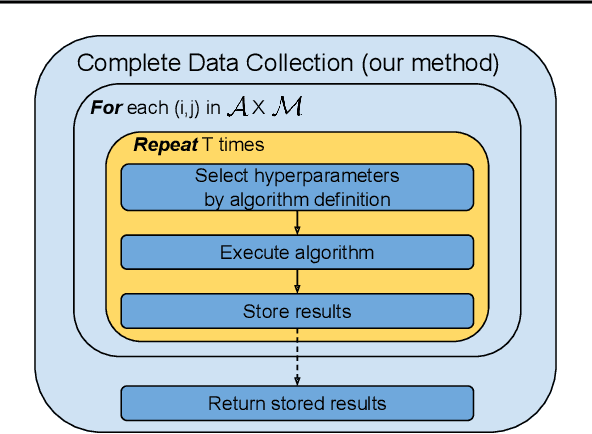
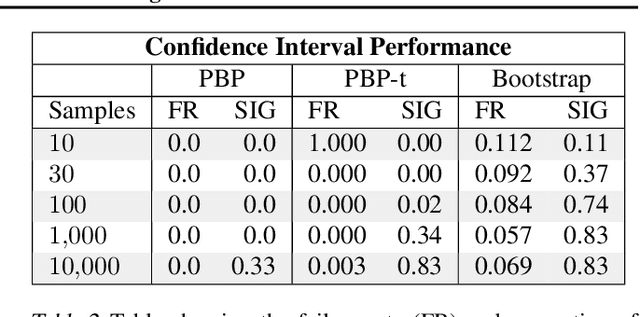
Performance evaluations are critical for quantifying algorithmic advances in reinforcement learning. Recent reproducibility analyses have shown that reported performance results are often inconsistent and difficult to replicate. In this work, we argue that the inconsistency of performance stems from the use of flawed evaluation metrics. Taking a step towards ensuring that reported results are consistent, we propose a new comprehensive evaluation methodology for reinforcement learning algorithms that produces reliable measurements of performance both on a single environment and when aggregated across environments. We demonstrate this method by evaluating a broad class of reinforcement learning algorithms on standard benchmark tasks.

Matching Questions and Answers in Dialogues from Online Forums

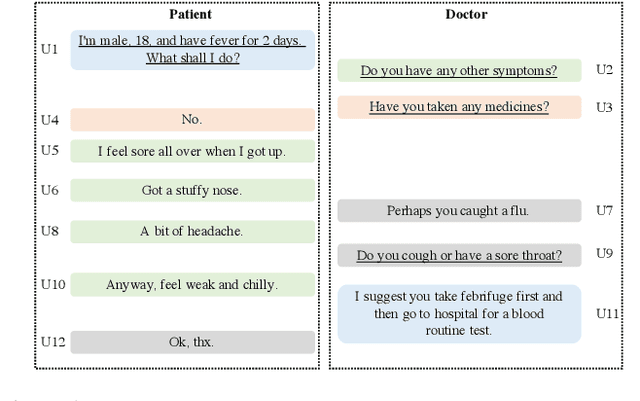
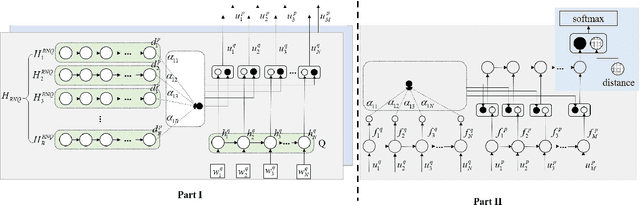
Matching question-answer relations between two turns in conversations is not only the first step in analyzing dialogue structures, but also valuable for training dialogue systems. This paper presents a QA matching model considering both distance information and dialogue history by two simultaneous attention mechanisms called mutual attention. Given scores computed by the trained model between each non-question turn with its candidate questions, a greedy matching strategy is used for final predictions. Because existing dialogue datasets such as the Ubuntu dataset are not suitable for the QA matching task, we further create a dataset with 1,000 labeled dialogues and demonstrate that our proposed model outperforms the state-of-the-art and other strong baselines, particularly for matching long-distance QA pairs.