Improving Calibration by Relating Focal Loss, Temperature Scaling, and Properness

Proper losses such as cross-entropy incentivize classifiers to produce class probabilities that are well-calibrated on the training data. Due to the generalization gap, these classifiers tend to become overconfident on the test data, mandating calibration methods such as temperature scaling. The focal loss is not proper, but training with it has been shown to often result in classifiers that are better calibrated on test data. Our first contribution is a simple explanation about why focal loss training often leads to better calibration than cross-entropy training. For this, we prove that focal loss can be decomposed into a confidence-raising transformation and a proper loss. This is why focal loss pushes the model to provide under-confident predictions on the training data, resulting in being better calibrated on the test data, due to the generalization gap. Secondly, we reveal a strong connection between temperature scaling and focal loss through its confidence-raising transformation, which we refer to as the focal calibration map. Thirdly, we propose focal temperature scaling - a new post-hoc calibration method combining focal calibration and temperature scaling. Our experiments on three image classification datasets demonstrate that focal temperature scaling outperforms standard temperature scaling.

Cautious Calibration in Binary Classification

Being cautious is crucial for enhancing the trustworthiness of machine learning systems integrated into decision-making pipelines. Although calibrated probabilities help in optimal decision-making, perfect calibration remains unattainable, leading to estimates that fluctuate between under- and overconfidence. This becomes a critical issue in high-risk scenarios, where even occasional overestimation can lead to extreme expected costs. In these scenarios, it is important for each predicted probability to lean towards underconfidence, rather than just achieving an average balance. In this study, we introduce the novel concept of cautious calibration in binary classification. This approach aims to produce probability estimates that are intentionally underconfident for each predicted probability. We highlight the importance of this approach in a high-risk scenario and propose a theoretically grounded method for learning cautious calibration maps. Through experiments, we explore and compare our method to various approaches, including methods originally not devised for cautious calibration but applicable in this context. We show that our approach is the most consistent in providing cautious estimates. Our work establishes a strong baseline for further developments in this novel framework.

Calibrated Perception Uncertainty Across Objects and Regions in Bird's-Eye-View

In driving scenarios with poor visibility or occlusions, it is important that the autonomous vehicle would take into account all the uncertainties when making driving decisions, including choice of a safe speed. The grid-based perception outputs, such as occupancy grids, and object-based outputs, such as lists of detected objects, must then be accompanied by well-calibrated uncertainty estimates. We highlight limitations in the state-of-the-art and propose a more complete set of uncertainties to be reported, particularly including undetected-object-ahead probabilities. We suggest a novel way to get these probabilistic outputs from bird's-eye-view probabilistic semantic segmentation, in the example of the FIERY model. We demonstrate that the obtained probabilities are not calibrated out-of-the-box and propose methods to achieve well-calibrated uncertainties.

On the Usefulness of the Fit-on-the-Test View on Evaluating Calibration of Classifiers

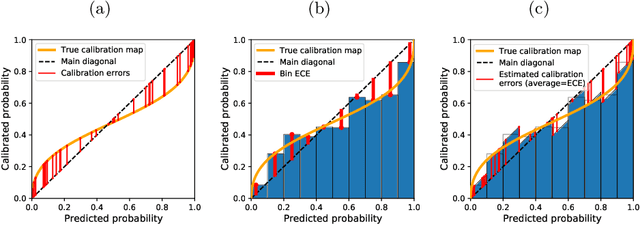
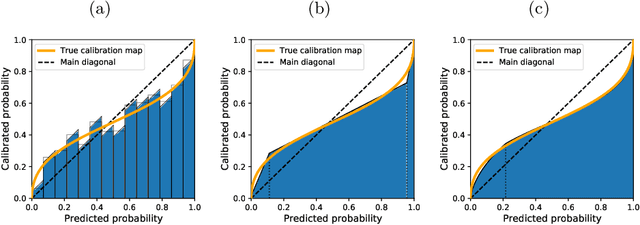
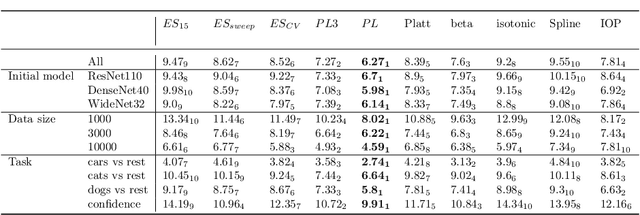
Every uncalibrated classifier has a corresponding true calibration map that calibrates its confidence. Deviations of this idealistic map from the identity map reveal miscalibration. Such calibration errors can be reduced with many post-hoc calibration methods which fit some family of calibration maps on a validation dataset. In contrast, evaluation of calibration with the expected calibration error (ECE) on the test set does not explicitly involve fitting. However, as we demonstrate, ECE can still be viewed as if fitting a family of functions on the test data. This motivates the fit-on-the-test view on evaluation: first, approximate a calibration map on the test data, and second, quantify its distance from the identity. Exploiting this view allows us to unlock missed opportunities: (1) use the plethora of post-hoc calibration methods for evaluating calibration; (2) tune the number of bins in ECE with cross-validation. Furthermore, we introduce: (3) benchmarking on pseudo-real data where the true calibration map can be estimated very precisely; and (4) novel calibration and evaluation methods using new calibration map families PL and PL3.

Ethical and Fairness Implications of Model Multiplicity

While predictive models are a purely technological feat, they may operate in a social context in which benign engineering choices entail unexpected real-life consequences. Fairness -- pertaining both to individuals and groups -- is one of such considerations; it surfaces when data capture protected characteristics of people who may be discriminated upon these attributes. This notion has predominantly been studied for a fixed predictive model, sometimes under different classification thresholds, striving to identify and eradicate its undesirable behaviour. Here we backtrack on this assumption and explore a novel definition of fairness where individuals can be harmed when one predictor is chosen ad hoc from a group of equally well performing models, i.e., in view of model multiplicity. Since a person may be classified differently across models that are otherwise considered equivalent, this individual could argue for a model with a more favourable outcome, possibly causing others to be adversely affected. We introduce this scenario with a two-dimensional example based on linear classification; then investigate its analytical properties in a broader context; and finally present experimental results on data sets popular in fairness studies. Our findings suggest that such unfairness can be found in real-life situations and may be difficult to mitigate with technical measures alone, as doing so degrades certain metrics of predictive performance.

Classifier Calibration: How to assess and improve predicted class probabilities: a survey

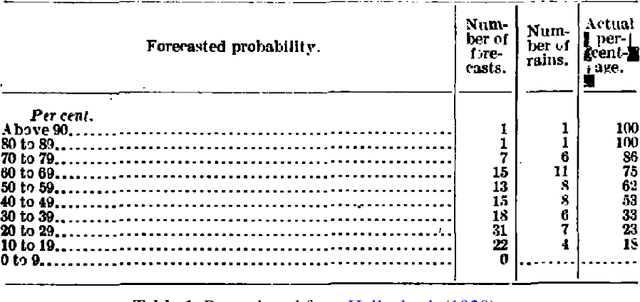
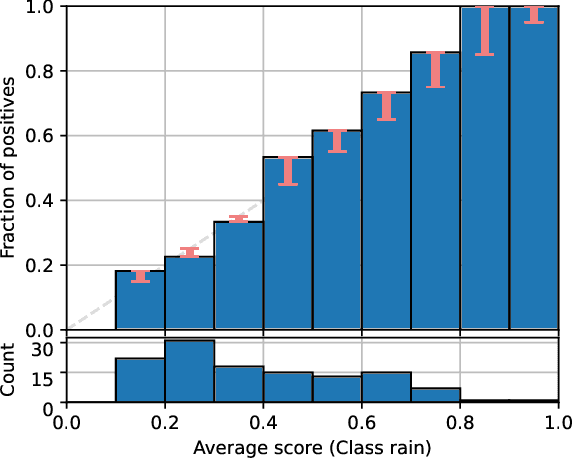
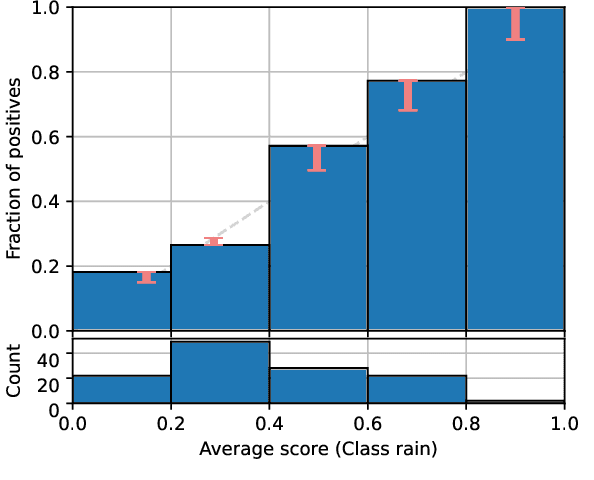
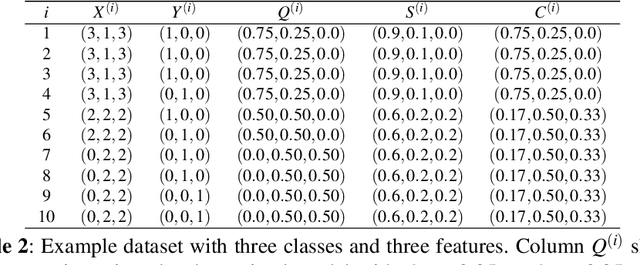
This paper provides both an introduction to and a detailed overview of the principles and practice of classifier calibration. A well-calibrated classifier correctly quantifies the level of uncertainty or confidence associated with its instance-wise predictions. This is essential for critical applications, optimal decision making, cost-sensitive classification, and for some types of context change. Calibration research has a rich history which predates the birth of machine learning as an academic field by decades. However, a recent increase in the interest on calibration has led to new methods and the extension from binary to the multiclass setting. The space of options and issues to consider is large, and navigating it requires the right set of concepts and tools. We provide both introductory material and up-to-date technical details of the main concepts and methods, including proper scoring rules and other evaluation metrics, visualisation approaches, a comprehensive account of post-hoc calibration methods for binary and multiclass classification, and several advanced topics.

Shift Happens: Adjusting Classifiers

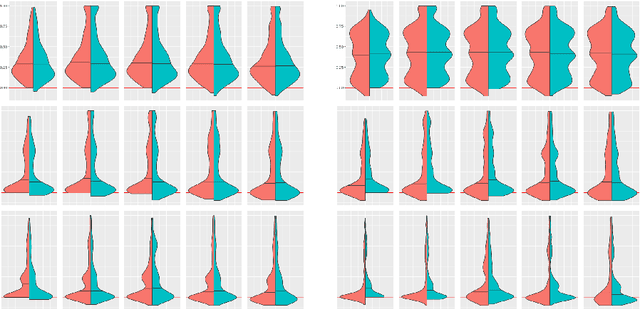
Minimizing expected loss measured by a proper scoring rule, such as Brier score or log-loss (cross-entropy), is a common objective while training a probabilistic classifier. If the data have experienced dataset shift where the class distributions change post-training, then often the model's performance will decrease, over-estimating the probabilities of some classes while under-estimating the others on average. We propose unbounded and bounded general adjustment (UGA and BGA) methods that transform all predictions to (re-)equalize the average prediction and the class distribution. These methods act differently depending on which proper scoring rule is to be minimized, and we have a theoretical guarantee of reducing loss on test data, if the exact class distribution is known. We also demonstrate experimentally that, when in practice the class distribution is known only approximately, there is often still a reduction in loss depending on the amount of shift and the precision to which the class distribution is known.

Instance-based Label Smoothing For Better Calibrated Classification Networks

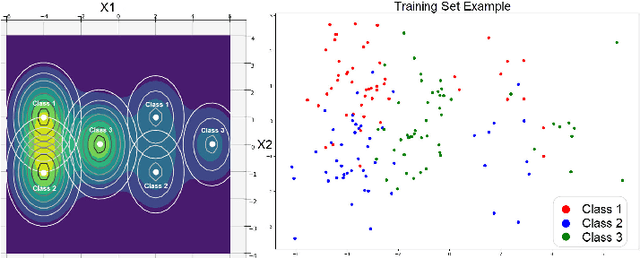
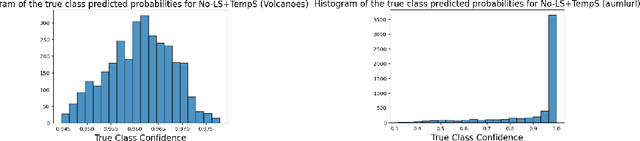
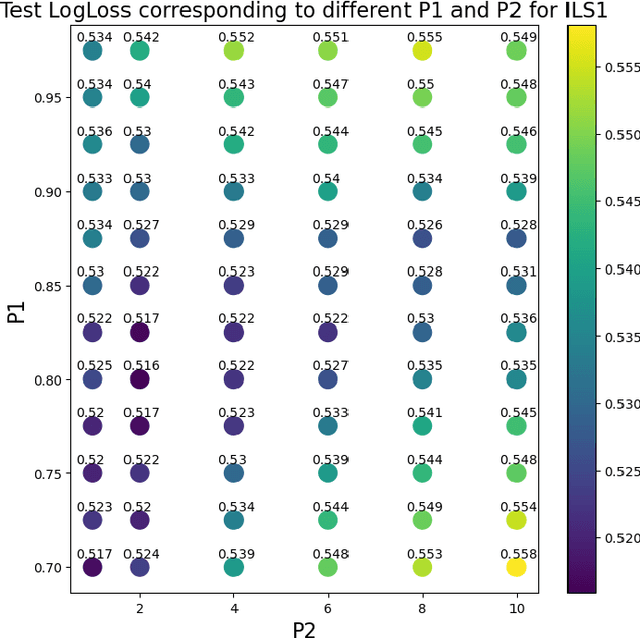
Label smoothing is widely used in deep neural networks for multi-class classification. While it enhances model generalization and reduces overconfidence by aiming to lower the probability for the predicted class, it distorts the predicted probabilities of other classes resulting in poor class-wise calibration. Another method for enhancing model generalization is self-distillation where the predictions of a teacher network trained with one-hot labels are used as the target for training a student network. We take inspiration from both label smoothing and self-distillation and propose two novel instance-based label smoothing approaches, where a teacher network trained with hard one-hot labels is used to determine the amount of per class smoothness applied to each instance. The assigned smoothing factor is non-uniformly distributed along with the classes according to their similarity with the actual class. Our methods show better generalization and calibration over standard label smoothing on various deep neural architectures and image classification datasets.

Correlated daily time series and forecasting in the M4 competition

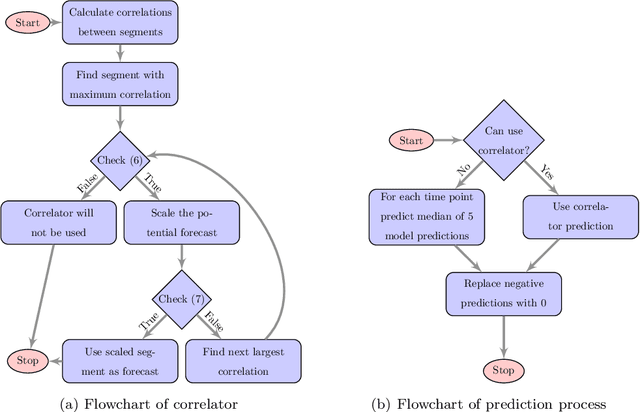
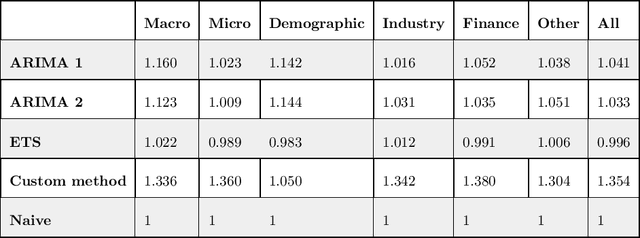
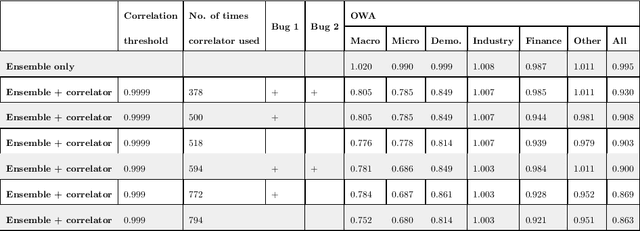
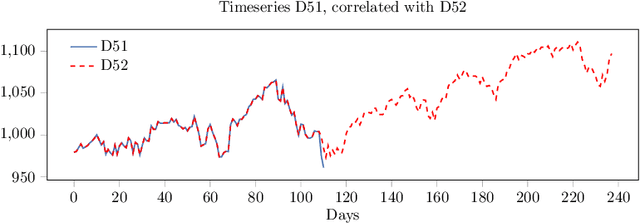
We participated in the M4 competition for time series forecasting and describe here our methods for forecasting daily time series. We used an ensemble of five statistical forecasting methods and a method that we refer to as the correlator. Our retrospective analysis using the ground truth values published by the M4 organisers after the competition demonstrates that the correlator was responsible for most of our gains over the naive constant forecasting method. We identify data leakage as one reason for its success, partly due to test data selected from different time intervals, and partly due to quality issues in the original time series. We suggest that future forecasting competitions should provide actual dates for the time series so that some of those leakages could be avoided by the participants.

Beyond temperature scaling: Obtaining well-calibrated multiclass probabilities with Dirichlet calibration

Class probabilities predicted by most multiclass classifiers are uncalibrated, often tending towards over-confidence. With neural networks, calibration can be improved by temperature scaling, a method to learn a single corrective multiplicative factor for inputs to the last softmax layer. On non-neural models the existing methods apply binary calibration in a pairwise or one-vs-rest fashion. We propose a natively multiclass calibration method applicable to classifiers from any model class, derived from Dirichlet distributions and generalising the beta calibration method from binary classification. It is easily implemented with neural nets since it is equivalent to log-transforming the uncalibrated probabilities, followed by one linear layer and softmax. Experiments demonstrate improved probabilistic predictions according to multiple measures (confidence-ECE, classwise-ECE, log-loss, Brier score) across a wide range of datasets and classifiers. Parameters of the learned Dirichlet calibration map provide insights to the biases in the uncalibrated model.