Classifier Calibration: How to assess and improve predicted class probabilities: a survey

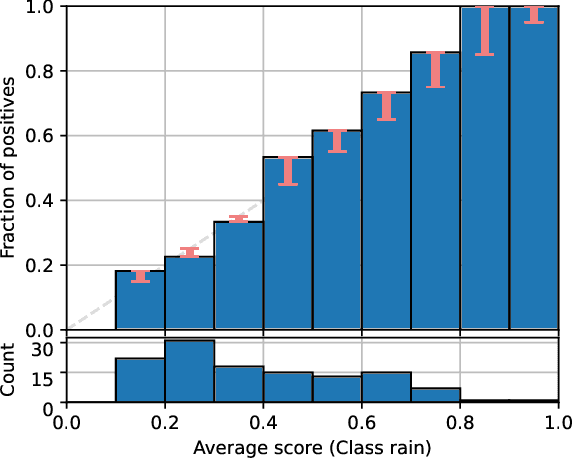
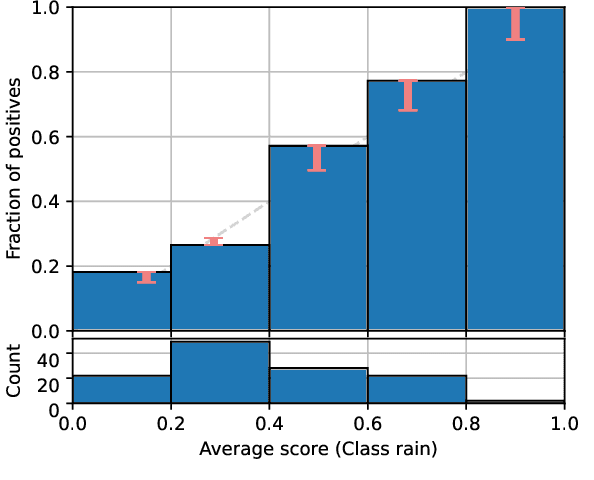
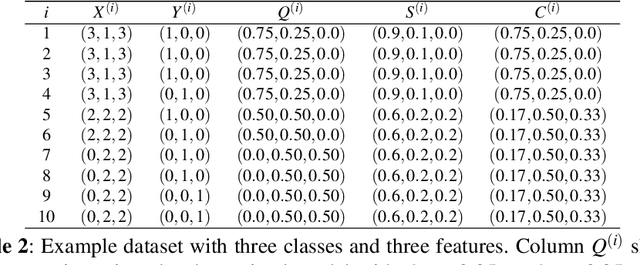
This paper provides both an introduction to and a detailed overview of the principles and practice of classifier calibration. A well-calibrated classifier correctly quantifies the level of uncertainty or confidence associated with its instance-wise predictions. This is essential for critical applications, optimal decision making, cost-sensitive classification, and for some types of context change. Calibration research has a rich history which predates the birth of machine learning as an academic field by decades. However, a recent increase in the interest on calibration has led to new methods and the extension from binary to the multiclass setting. The space of options and issues to consider is large, and navigating it requires the right set of concepts and tools. We provide both introductory material and up-to-date technical details of the main concepts and methods, including proper scoring rules and other evaluation metrics, visualisation approaches, a comprehensive account of post-hoc calibration methods for binary and multiclass classification, and several advanced topics.

Beyond temperature scaling: Obtaining well-calibrated multiclass probabilities with Dirichlet calibration

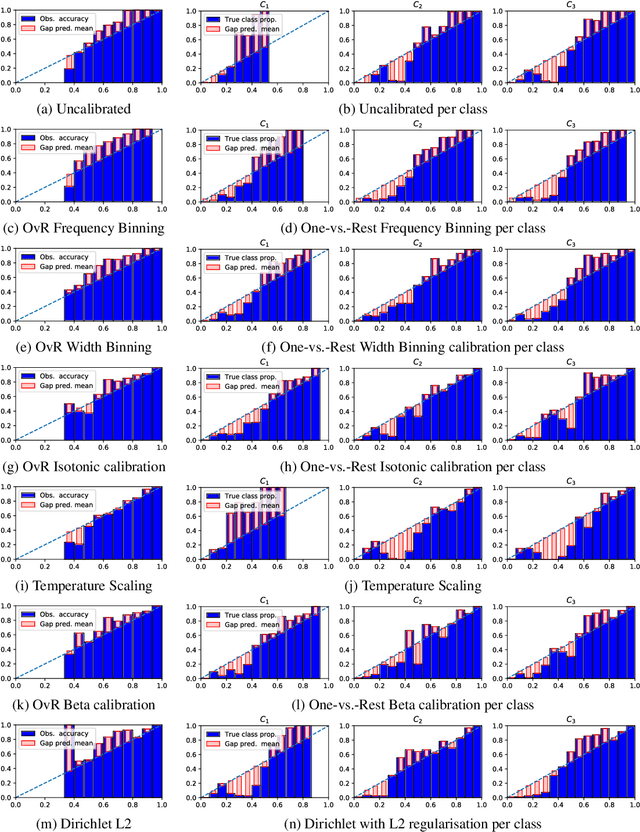
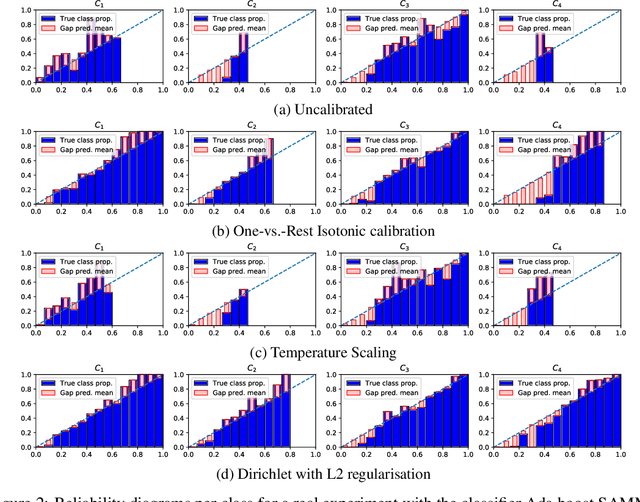
Class probabilities predicted by most multiclass classifiers are uncalibrated, often tending towards over-confidence. With neural networks, calibration can be improved by temperature scaling, a method to learn a single corrective multiplicative factor for inputs to the last softmax layer. On non-neural models the existing methods apply binary calibration in a pairwise or one-vs-rest fashion. We propose a natively multiclass calibration method applicable to classifiers from any model class, derived from Dirichlet distributions and generalising the beta calibration method from binary classification. It is easily implemented with neural nets since it is equivalent to log-transforming the uncalibrated probabilities, followed by one linear layer and softmax. Experiments demonstrate improved probabilistic predictions according to multiple measures (confidence-ECE, classwise-ECE, log-loss, Brier score) across a wide range of datasets and classifiers. Parameters of the learned Dirichlet calibration map provide insights to the biases in the uncalibrated model.

$β^3$-IRT: A New Item Response Model and its Applications

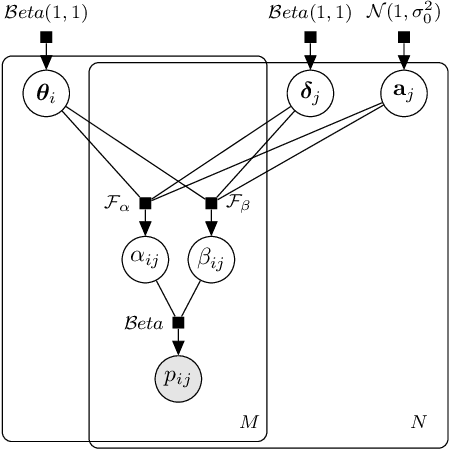
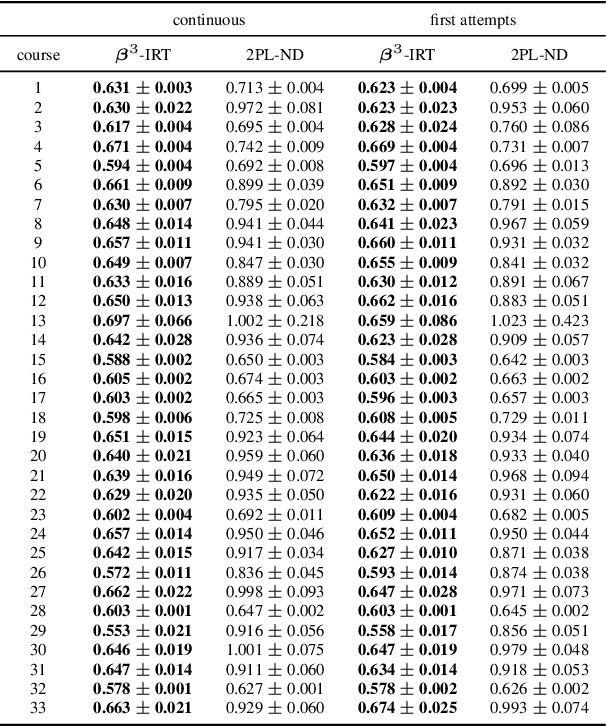
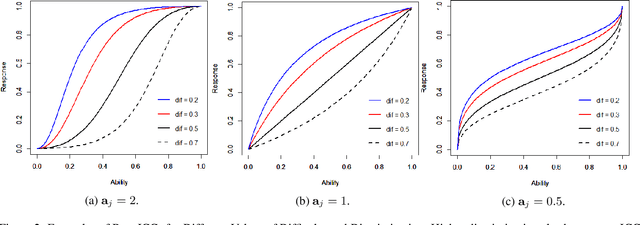
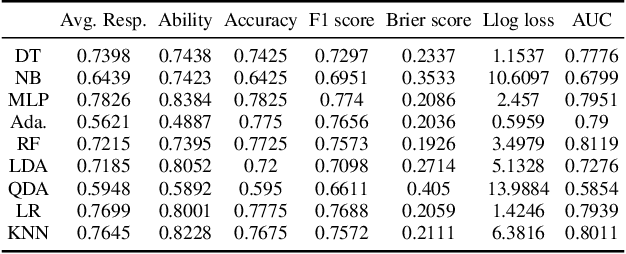
Item Response Theory (IRT) aims to assess latent abilities of respondents based on the correctness of their answers in aptitude test items with different difficulty levels. In this paper, we propose the $\beta^3$-IRT model, which models continuous responses and can generate a much enriched family of Item Characteristic Curve (ICC). In experiments we applied the proposed model to data from an online exam platform, and show our model outperforms a more standard 2PL-ND model on all datasets. Furthermore, we show how to apply $\beta^3$-IRT to assess the ability of machine learning classifiers. This novel application results in a new metric for evaluating the quality of the classifier's probability estimates, based on the inferred difficulty and discrimination of data instances.