Explanation-by-Example Based on Item Response Theory

Intelligent systems that use Machine Learning classification algorithms are increasingly common in everyday society. However, many systems use black-box models that do not have characteristics that allow for self-explanation of their predictions. This situation leads researchers in the field and society to the following question: How can I trust the prediction of a model I cannot understand? In this sense, XAI emerges as a field of AI that aims to create techniques capable of explaining the decisions of the classifier to the end-user. As a result, several techniques have emerged, such as Explanation-by-Example, which has a few initiatives consolidated by the community currently working with XAI. This research explores the Item Response Theory (IRT) as a tool to explaining the models and measuring the level of reliability of the Explanation-by-Example approach. To this end, four datasets with different levels of complexity were used, and the Random Forest model was used as a hypothesis test. From the test set, 83.8% of the errors are from instances in which the IRT points out the model as unreliable.

Label noise detection under the Noise at Random model with ensemble filters

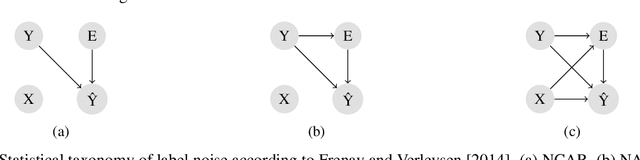
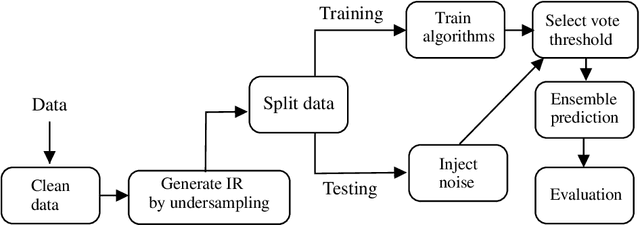
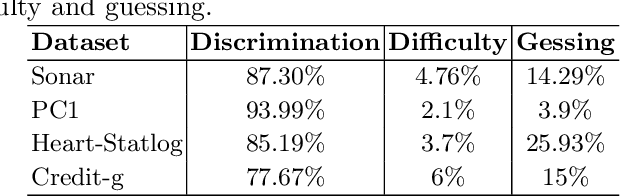
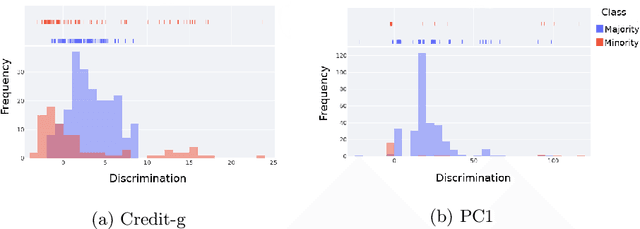
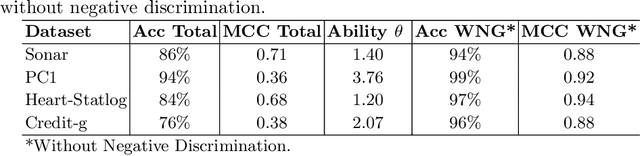
Label noise detection has been widely studied in Machine Learning because of its importance in improving training data quality. Satisfactory noise detection has been achieved by adopting ensembles of classifiers. In this approach, an instance is assigned as mislabeled if a high proportion of members in the pool misclassifies it. Previous authors have empirically evaluated this approach; nevertheless, they mostly assumed that label noise is generated completely at random in a dataset. This is a strong assumption since other types of label noise are feasible in practice and can influence noise detection results. This work investigates the performance of ensemble noise detection under two different noise models: the Noisy at Random (NAR), in which the probability of label noise depends on the instance class, in comparison to the Noisy Completely at Random model, in which the probability of label noise is entirely independent. In this setting, we investigate the effect of class distribution on noise detection performance since it changes the total noise level observed in a dataset under the NAR assumption. Further, an evaluation of the ensemble vote threshold is conducted to contrast with the most common approaches in the literature. In many performed experiments, choosing a noise generation model over another can lead to different results when considering aspects such as class imbalance and noise level ratio among different classes.

Data vs classifiers, who wins?

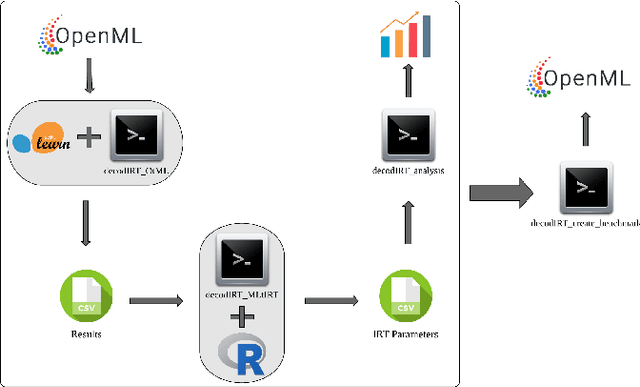
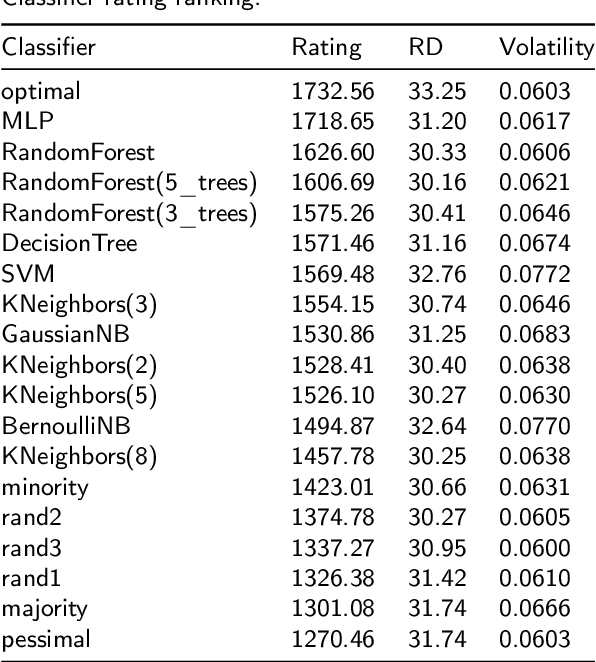
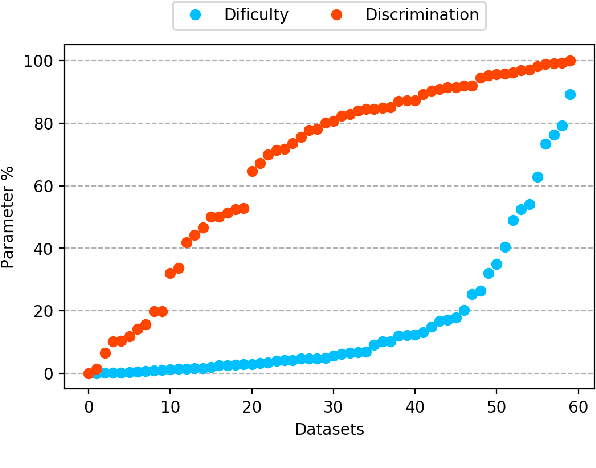
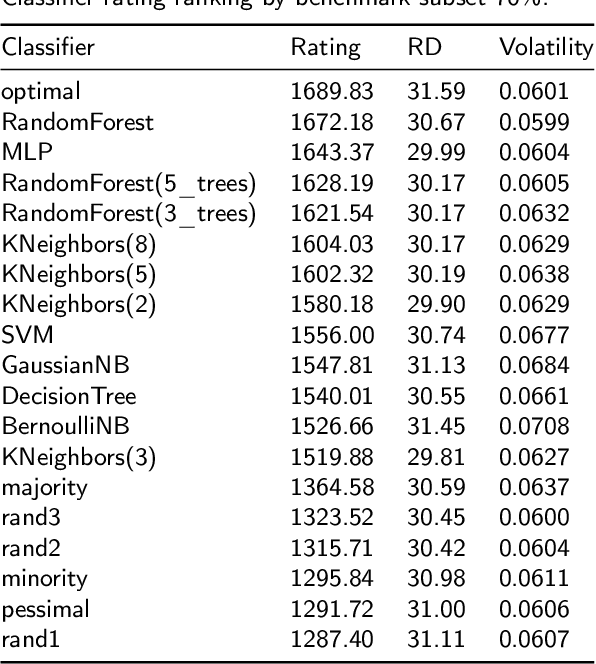
The classification experiments covered by machine learning (ML) are composed by two important parts: the data and the algorithm. As they are a fundamental part of the problem, both must be considered when evaluating a model's performance against a benchmark. The best classifiers need robust benchmarks to be properly evaluated. For this, gold standard benchmarks such as OpenML-CC18 are used. However, data complexity is commonly not considered along with the model during a performance evaluation. Recent studies employ Item Response Theory (IRT) as a new approach to evaluating datasets and algorithms, capable of evaluating both simultaneously. This work presents a new evaluation methodology based on IRT and Glicko-2, jointly with the decodIRT tool developed to guide the estimation of IRT in ML. It explores the IRT as a tool to evaluate the OpenML-CC18 benchmark for its algorithmic evaluation capability and checks if there is a subset of datasets more efficient than the original benchmark. Several classifiers, from classics to ensemble, are also evaluated using the IRT models. The Glicko-2 rating system was applied together with IRT to summarize the innate ability and classifiers performance. It was noted that not all OpenML-CC18 datasets are really useful for evaluating algorithms, where only 10% were rated as being really difficult. Furthermore, it was verified the existence of a more efficient subset containing only 50% of the original size. While Randon Forest was singled out as the algorithm with the best innate ability.

Decoding machine learning benchmarks

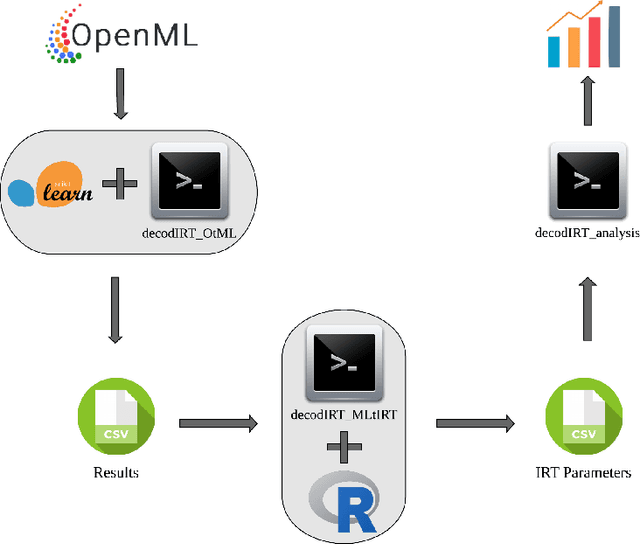
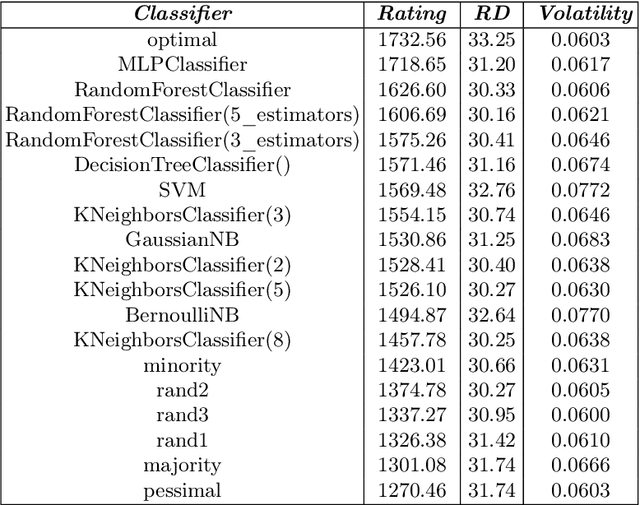
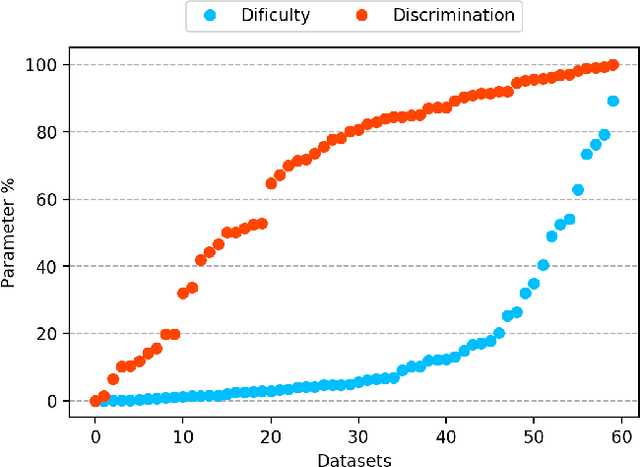
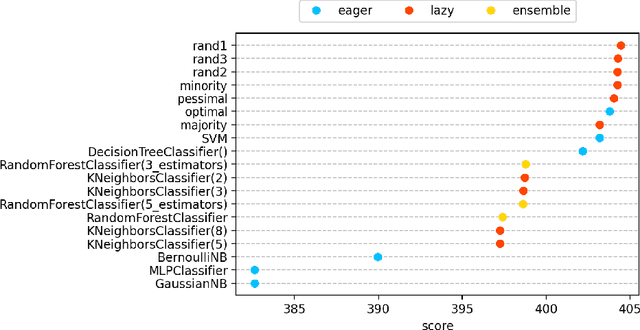
Despite the availability of benchmark machine learning (ML) repositories (e.g., UCI, OpenML), there is no standard evaluation strategy yet capable of pointing out which is the best set of datasets to serve as gold standard to test different ML algorithms. In recent studies, Item Response Theory (IRT) has emerged as a new approach to elucidate what should be a good ML benchmark. This work applied IRT to explore the well-known OpenML-CC18 benchmark to identify how suitable it is on the evaluation of classifiers. Several classifiers ranging from classical to ensembles ones were evaluated using IRT models, which could simultaneously estimate dataset difficulty and classifiers' ability. The Glicko-2 rating system was applied on the top of IRT to summarize the innate ability and aptitude of classifiers. It was observed that not all datasets from OpenML-CC18 are really useful to evaluate classifiers. Most datasets evaluated in this work (84%) contain easy instances in general (e.g., around 10% of difficult instances only). Also, 80% of the instances in half of this benchmark are very discriminating ones, which can be of great use for pairwise algorithm comparison, but not useful to push classifiers abilities. This paper presents this new evaluation methodology based on IRT as well as the tool decodIRT, developed to guide IRT estimation over ML benchmarks.

$β^3$-IRT: A New Item Response Model and its Applications

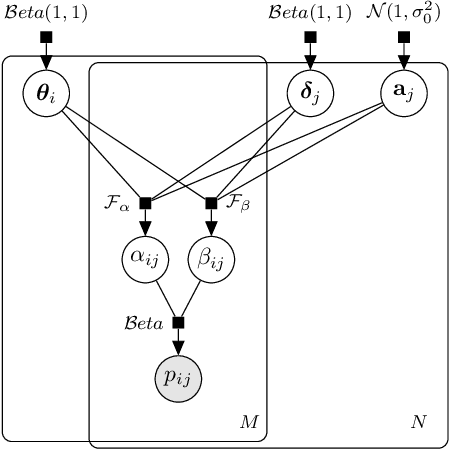
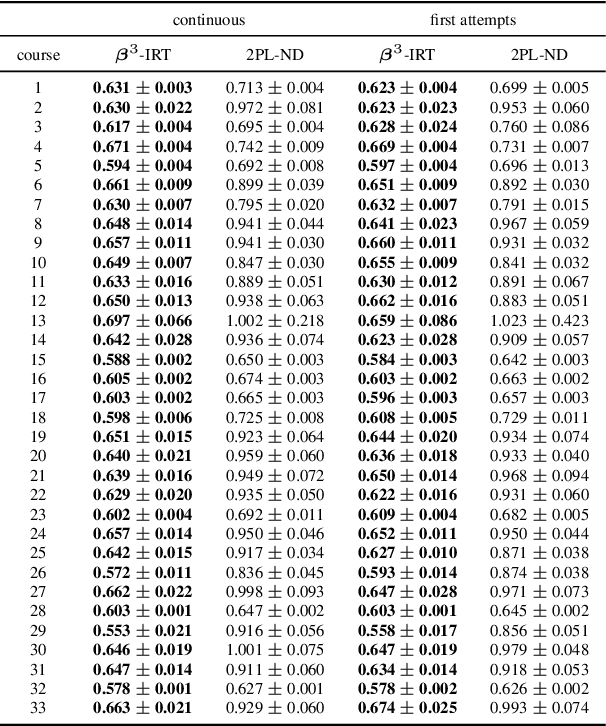
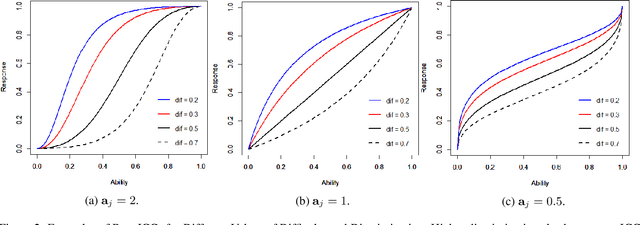
Item Response Theory (IRT) aims to assess latent abilities of respondents based on the correctness of their answers in aptitude test items with different difficulty levels. In this paper, we propose the $\beta^3$-IRT model, which models continuous responses and can generate a much enriched family of Item Characteristic Curve (ICC). In experiments we applied the proposed model to data from an online exam platform, and show our model outperforms a more standard 2PL-ND model on all datasets. Furthermore, we show how to apply $\beta^3$-IRT to assess the ability of machine learning classifiers. This novel application results in a new metric for evaluating the quality of the classifier's probability estimates, based on the inferred difficulty and discrimination of data instances.