Cautious Calibration in Binary Classification

Being cautious is crucial for enhancing the trustworthiness of machine learning systems integrated into decision-making pipelines. Although calibrated probabilities help in optimal decision-making, perfect calibration remains unattainable, leading to estimates that fluctuate between under- and overconfidence. This becomes a critical issue in high-risk scenarios, where even occasional overestimation can lead to extreme expected costs. In these scenarios, it is important for each predicted probability to lean towards underconfidence, rather than just achieving an average balance. In this study, we introduce the novel concept of cautious calibration in binary classification. This approach aims to produce probability estimates that are intentionally underconfident for each predicted probability. We highlight the importance of this approach in a high-risk scenario and propose a theoretically grounded method for learning cautious calibration maps. Through experiments, we explore and compare our method to various approaches, including methods originally not devised for cautious calibration but applicable in this context. We show that our approach is the most consistent in providing cautious estimates. Our work establishes a strong baseline for further developments in this novel framework.

Shift Happens: Adjusting Classifiers

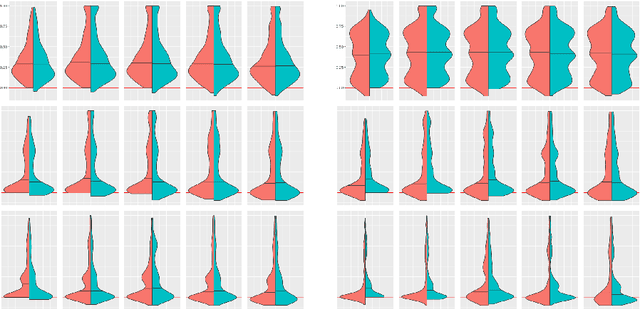
Minimizing expected loss measured by a proper scoring rule, such as Brier score or log-loss (cross-entropy), is a common objective while training a probabilistic classifier. If the data have experienced dataset shift where the class distributions change post-training, then often the model's performance will decrease, over-estimating the probabilities of some classes while under-estimating the others on average. We propose unbounded and bounded general adjustment (UGA and BGA) methods that transform all predictions to (re-)equalize the average prediction and the class distribution. These methods act differently depending on which proper scoring rule is to be minimized, and we have a theoretical guarantee of reducing loss on test data, if the exact class distribution is known. We also demonstrate experimentally that, when in practice the class distribution is known only approximately, there is often still a reduction in loss depending on the amount of shift and the precision to which the class distribution is known.