Matthew Staib
Distributionally Robust Optimization and Generalization in Kernel Methods
May 27, 2019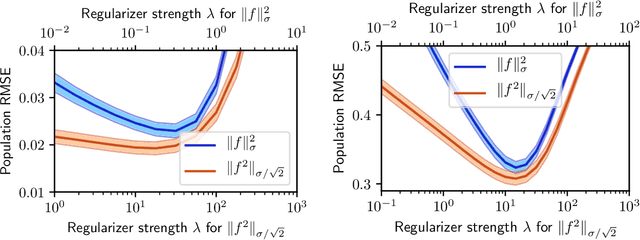
Abstract:Distributionally robust optimization (DRO) has attracted attention in machine learning due to its connections to regularization, generalization, and robustness. Existing work has considered uncertainty sets based on phi-divergences and Wasserstein distances, each of which have drawbacks. In this paper, we study DRO with uncertainty sets measured via maximum mean discrepancy (MMD). We show that MMD DRO is roughly equivalent to regularization by the Hilbert norm and, as a byproduct, reveal deep connections to classic results in statistical learning. In particular, we obtain an alternative proof of a generalization bound for Gaussian kernel ridge regression via a DRO lense. The proof also suggests a new regularizer. Our results apply beyond kernel methods: we derive a generically applicable approximation of MMD DRO, and show that it generalizes recent work on variance-based regularization.
Escaping Saddle Points with Adaptive Gradient Methods
Jan 26, 2019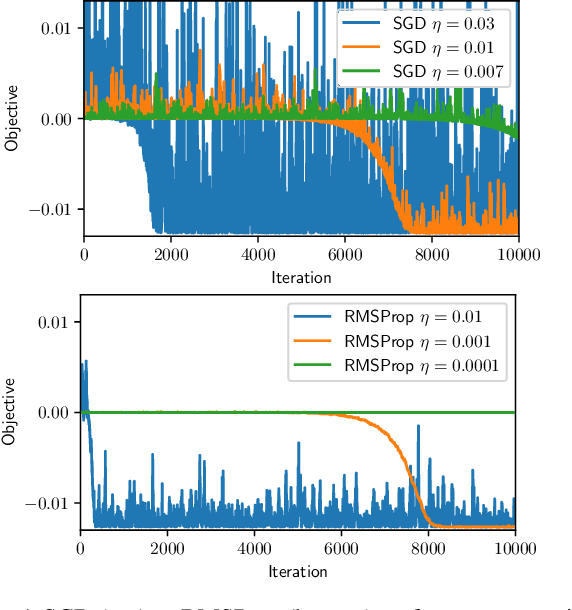
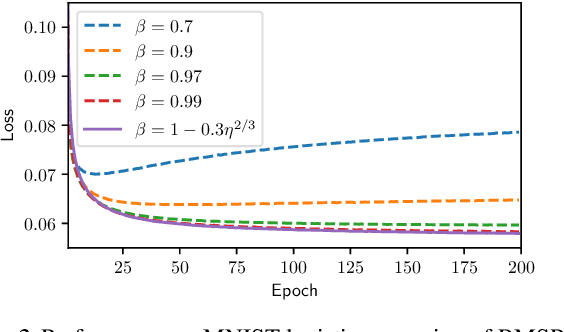
Abstract:Adaptive methods such as Adam and RMSProp are widely used in deep learning but are not well understood. In this paper, we seek a crisp, clean and precise characterization of their behavior in nonconvex settings. To this end, we first provide a novel view of adaptive methods as preconditioned SGD, where the preconditioner is estimated in an online manner. By studying the preconditioner on its own, we elucidate its purpose: it rescales the stochastic gradient noise to be isotropic near stationary points, which helps escape saddle points. Furthermore, we show that adaptive methods can efficiently estimate the aforementioned preconditioner. By gluing together these two components, we provide the first (to our knowledge) second-order convergence result for any adaptive method. The key insight from our analysis is that, compared to SGD, adaptive methods escape saddle points faster, and can converge faster overall to second-order stationary points.
Inorganic Materials Synthesis Planning with Literature-Trained Neural Networks
Dec 31, 2018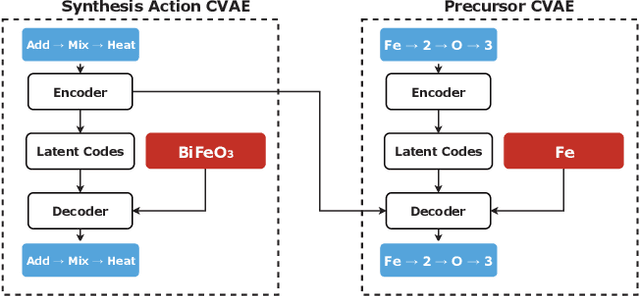
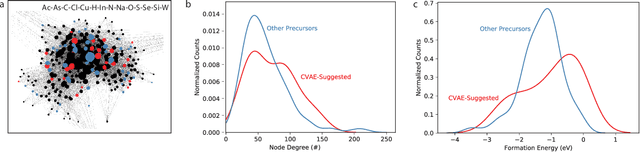
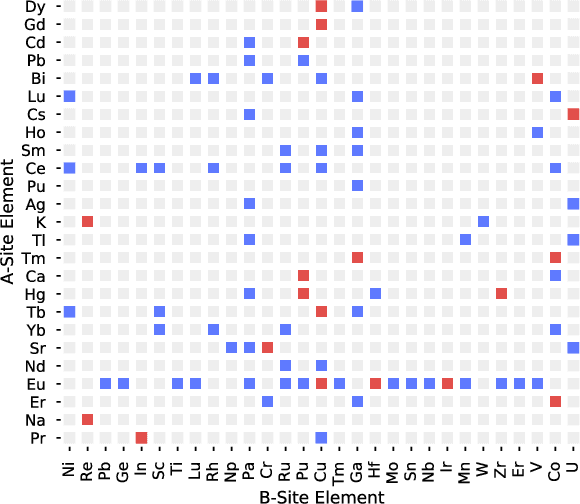

Abstract:Leveraging new data sources is a key step in accelerating the pace of materials design and discovery. To complement the strides in synthesis planning driven by historical, experimental, and computed data, we present an automated method for connecting scientific literature to synthesis insights. Starting from natural language text, we apply word embeddings from language models, which are fed into a named entity recognition model, upon which a conditional variational autoencoder is trained to generate syntheses for arbitrary materials. We show the potential of this technique by predicting precursors for two perovskite materials, using only training data published over a decade prior to their first reported syntheses. We demonstrate that the model learns representations of materials corresponding to synthesis-related properties, and that the model's behavior complements existing thermodynamic knowledge. Finally, we apply the model to perform synthesizability screening for proposed novel perovskite compounds.
Distributionally Robust Submodular Maximization
Jun 06, 2018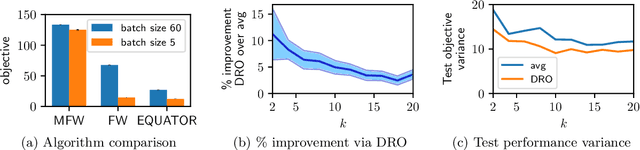
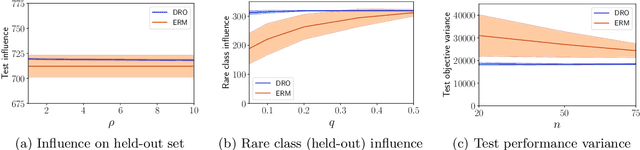
Abstract:Submodular functions have applications throughout machine learning, but in many settings, we do not have direct access to the underlying function $f$. We focus on stochastic functions that are given as an expectation of functions over a distribution $P$. In practice, we often have only a limited set of samples $f_i$ from $P$. The standard approach indirectly optimizes $f$ by maximizing the sum of $f_i$. However, this ignores generalization to the true (unknown) distribution. In this paper, we achieve better performance on the actual underlying function $f$ by directly optimizing a combination of bias and variance. Algorithmically, we accomplish this by showing how to carry out distributionally robust optimization (DRO) for submodular functions, providing efficient algorithms backed by theoretical guarantees which leverage several novel contributions to the general theory of DRO. We also show compelling empirical evidence that DRO improves generalization to the unknown stochastic submodular function.
Parallel Streaming Wasserstein Barycenters
Nov 14, 2017

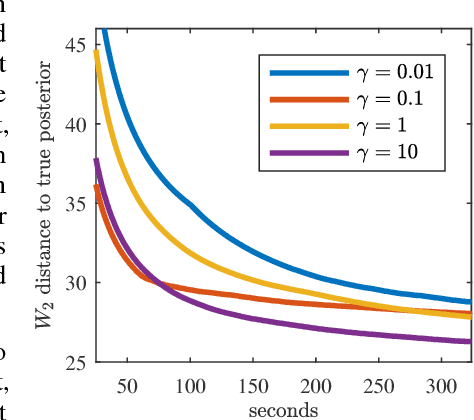
Abstract:Efficiently aggregating data from different sources is a challenging problem, particularly when samples from each source are distributed differently. These differences can be inherent to the inference task or present for other reasons: sensors in a sensor network may be placed far apart, affecting their individual measurements. Conversely, it is computationally advantageous to split Bayesian inference tasks across subsets of data, but data need not be identically distributed across subsets. One principled way to fuse probability distributions is via the lens of optimal transport: the Wasserstein barycenter is a single distribution that summarizes a collection of input measures while respecting their geometry. However, computing the barycenter scales poorly and requires discretization of all input distributions and the barycenter itself. Improving on this situation, we present a scalable, communication-efficient, parallel algorithm for computing the Wasserstein barycenter of arbitrary distributions. Our algorithm can operate directly on continuous input distributions and is optimized for streaming data. Our method is even robust to nonstationary input distributions and produces a barycenter estimate that tracks the input measures over time. The algorithm is semi-discrete, needing to discretize only the barycenter estimate. To the best of our knowledge, we also provide the first bounds on the quality of the approximate barycenter as the discretization becomes finer. Finally, we demonstrate the practical effectiveness of our method, both in tracking moving distributions on a sphere, as well as in a large-scale Bayesian inference task.
Robust Budget Allocation via Continuous Submodular Functions
Jun 13, 2017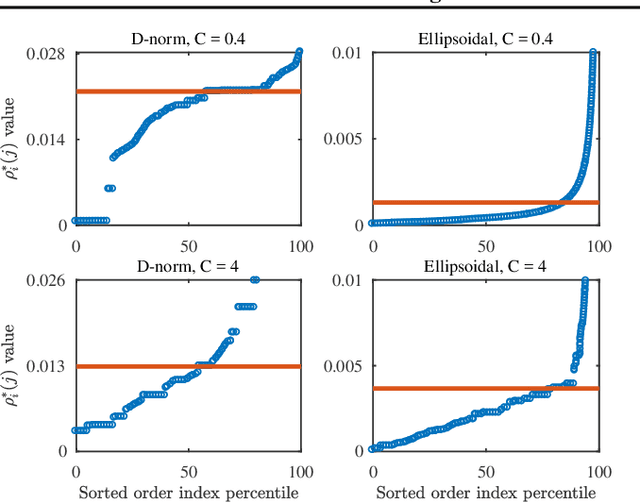
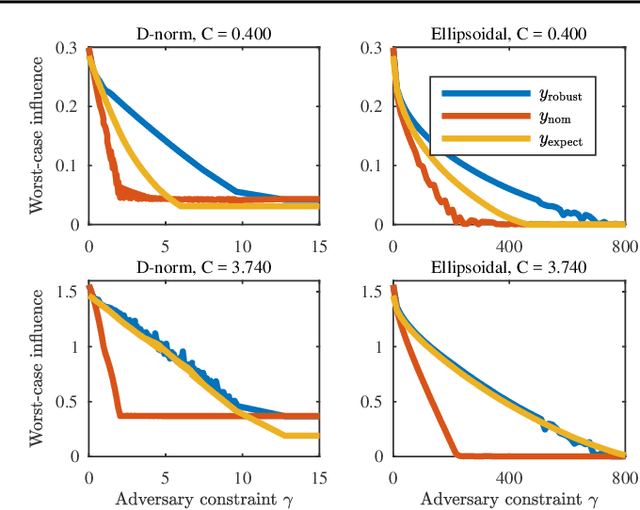
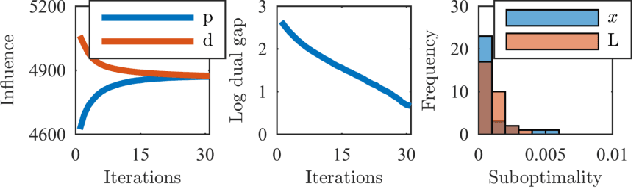
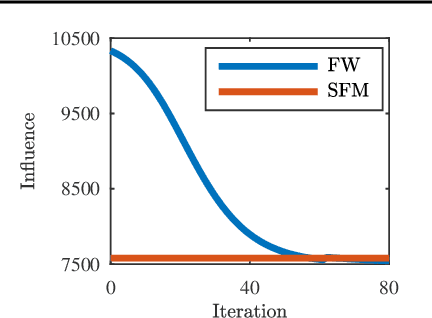
Abstract:The optimal allocation of resources for maximizing influence, spread of information or coverage, has gained attention in the past years, in particular in machine learning and data mining. But in applications, the parameters of the problem are rarely known exactly, and using wrong parameters can lead to undesirable outcomes. We hence revisit a continuous version of the Budget Allocation or Bipartite Influence Maximization problem introduced by Alon et al. (2012) from a robust optimization perspective, where an adversary may choose the least favorable parameters within a confidence set. The resulting problem is a nonconvex-concave saddle point problem (or game). We show that this nonconvex problem can be solved exactly by leveraging connections to continuous submodular functions, and by solving a constrained submodular minimization problem. Although constrained submodular minimization is hard in general, here, we establish conditions under which such a problem can be solved to arbitrary precision $\epsilon$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge