Escaping Saddle Points with Adaptive Gradient Methods
Paper and Code
Jan 26, 2019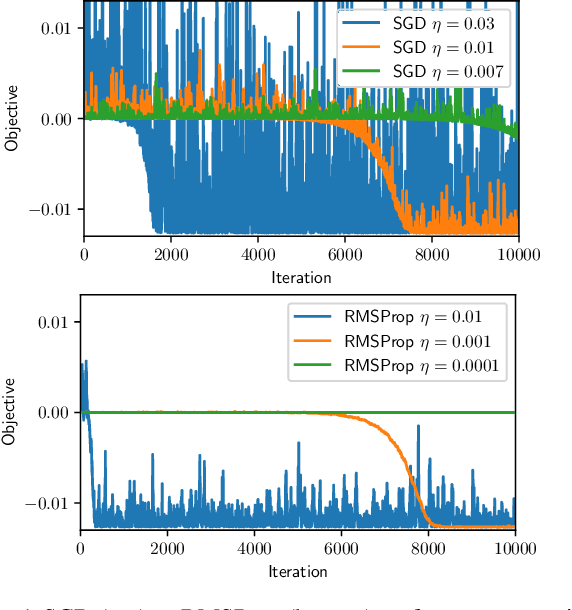
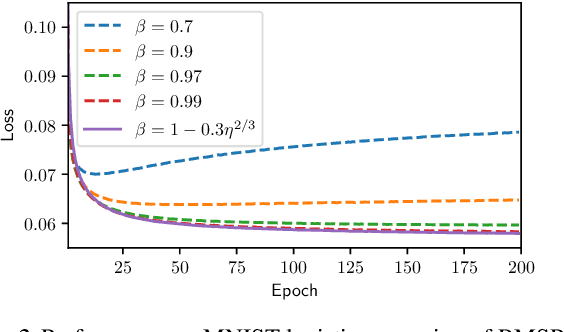
Adaptive methods such as Adam and RMSProp are widely used in deep learning but are not well understood. In this paper, we seek a crisp, clean and precise characterization of their behavior in nonconvex settings. To this end, we first provide a novel view of adaptive methods as preconditioned SGD, where the preconditioner is estimated in an online manner. By studying the preconditioner on its own, we elucidate its purpose: it rescales the stochastic gradient noise to be isotropic near stationary points, which helps escape saddle points. Furthermore, we show that adaptive methods can efficiently estimate the aforementioned preconditioner. By gluing together these two components, we provide the first (to our knowledge) second-order convergence result for any adaptive method. The key insight from our analysis is that, compared to SGD, adaptive methods escape saddle points faster, and can converge faster overall to second-order stationary points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge