Certified Invertibility in Neural Networks via Mixed-Integer Programming

Neural networks are notoriously vulnerable to adversarial attacks -- small imperceptible perturbations that can change the network's output drastically. In the reverse direction, there may exist large, meaningful perturbations that leave the network's decision unchanged (excessive invariance, nonivertibility). We study the latter phenomenon in two contexts: (a) discrete-time dynamical system identification, as well as (b) calibration of the output of one neural network to the output of another (neural network matching). For ReLU networks and $L_p$ norms ($p=1,2,\infty$), we formulate these optimization problems as mixed-integer programs (MIPs) that apply to neural network approximators of dynamical systems. We also discuss the applicability of our results to invertibility certification in transformations between neural networks (e.g. at different levels of pruning).

Learning to Control Linear Systems can be Hard

In this paper, we study the statistical difficulty of learning to control linear systems. We focus on two standard benchmarks, the sample complexity of stabilization, and the regret of the online learning of the Linear Quadratic Regulator (LQR). Prior results state that the statistical difficulty for both benchmarks scales polynomially with the system state dimension up to system-theoretic quantities. However, this does not reveal the whole picture. By utilizing minimax lower bounds for both benchmarks, we prove that there exist non-trivial classes of systems for which learning complexity scales dramatically, i.e. exponentially, with the system dimension. This situation arises in the case of underactuated systems, i.e. systems with fewer inputs than states. Such systems are structurally difficult to control and their system theoretic quantities can scale exponentially with the system dimension dominating learning complexity. Under some additional structural assumptions (bounding systems away from uncontrollability), we provide qualitatively matching upper bounds. We prove that learning complexity can be at most exponential with the controllability index of the system, that is the degree of underactuation.

Adaptive Stochastic MPC under Unknown Noise Distribution

In this paper, we address the stochastic MPC (SMPC) problem for linear systems, subject to chance state constraints and hard input constraints, under unknown noise distribution. First, we reformulate the chance state constraints as deterministic constraints depending only on explicit noise statistics. Based on these reformulated constraints, we design a distributionally robust and robustly stable benchmark SMPC algorithm for the ideal setting of known noise statistics. Then, we employ this benchmark controller to derive a novel robustly stable adaptive SMPC scheme that learns the necessary noise statistics online, while guaranteeing time-uniform satisfaction of the unknown reformulated state constraints with high probability. The latter is achieved through the use of confidence intervals which rely on the empirical noise statistics and are valid uniformly over time. Moreover, control performance is improved over time as more noise samples are gathered and better estimates of the noise statistics are obtained, given the online adaptation of the estimated reformulated constraints. Additionally, in tracking problems with multiple successive targets our approach leads to an online-enlarged domain of attraction compared to robust tube-based MPC. A numerical simulation of a DC-DC converter is used to demonstrate the effectiveness of the developed methodology.

Stability Analysis of Complementarity Systems with Neural Network Controllers

Complementarity problems, a class of mathematical optimization problems with orthogonality constraints, are widely used in many robotics tasks, such as locomotion and manipulation, due to their ability to model non-smooth phenomena (e.g., contact dynamics). In this paper, we propose a method to analyze the stability of complementarity systems with neural network controllers. First, we introduce a method to represent neural networks with rectified linear unit (ReLU) activations as the solution to a linear complementarity problem. Then, we show that systems with ReLU network controllers have an equivalent linear complementarity system (LCS) description. Using the LCS representation, we turn the stability verification problem into a linear matrix inequality (LMI) feasibility problem. We demonstrate the approach on several examples, including multi-contact problems and friction models with non-unique solutions.

Learning to Track Dynamic Targets in Partially Known Environments

We solve active target tracking, one of the essential tasks in autonomous systems, using a deep reinforcement learning (RL) approach. In this problem, an autonomous agent is tasked with acquiring information about targets of interests using its onboard sensors. The classical challenges in this problem are system model dependence and the difficulty of computing information-theoretic cost functions for a long planning horizon. RL provides solutions for these challenges as the length of its effective planning horizon does not affect the computational complexity, and it drops the strong dependency of an algorithm on system models. In particular, we introduce Active Tracking Target Network (ATTN), a unified RL policy that is capable of solving major sub-tasks of active target tracking -- in-sight tracking, navigation, and exploration. The policy shows robust behavior for tracking agile and anomalous targets with a partially known target model. Additionally, the same policy is able to navigate in obstacle environments to reach distant targets as well as explore the environment when targets are positioned in unexpected locations.

BayesRace: Learning to race autonomously using prior experience

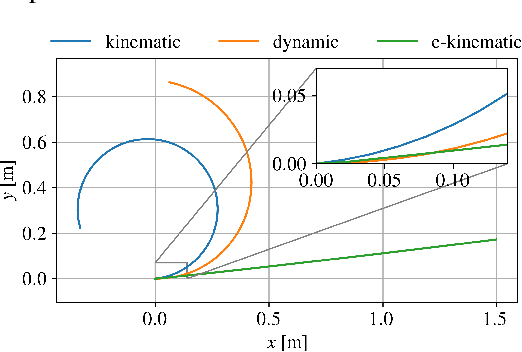
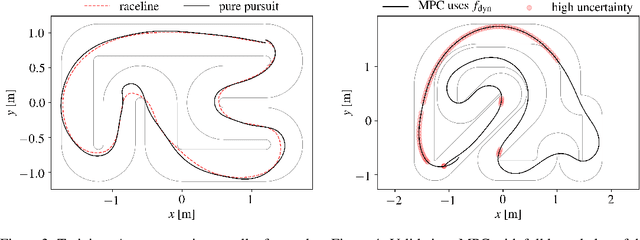
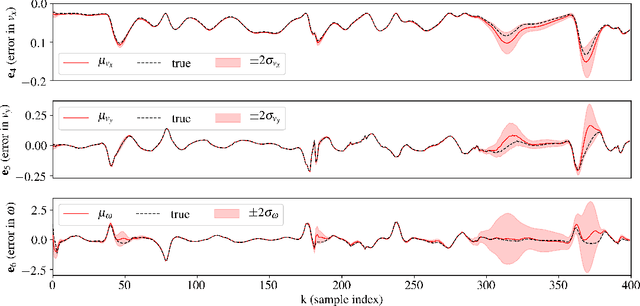
Learning to race autonomously is a challenging problem. It requires perception, estimation, planning, and control to work together in synchronization while driving at the limit of a vehicle's handling capability. Among others, one of the fundamental challenges lies in predicting the vehicle's future states like position, orientation, and speed with high accuracy because it is inevitably hard to identify vehicle model parameters that capture its real nonlinear dynamics in the presence of lateral tire slip. We present a model-based planning and control framework for autonomous racing that significantly reduces the effort required in system identification. Our approach bridges the gap between the design in a simulation and the real world by learning from on-board sensor measurements. Thus, the teams participating in autonomous racing competitions can start racing on new tracks without having to worry about tuning the vehicle model.

Reach-SDP: Reachability Analysis of Closed-Loop Systems with Neural Network Controllers via Semidefinite Programming

There has been an increasing interest in using neural networks in closed-loop control systems to improve performance and reduce computational costs for on-line implementation. However, providing safety and stability guarantees for these systems is challenging due to the nonlinear and compositional structure of neural networks. In this paper, we propose a novel forward reachability analysis method for the safety verification of linear time-varying systems with neural networks in feedback interconnection. Our technical approach relies on abstracting the nonlinear activation functions by quadratic constraints, which leads to an outer-approximation of forward reachable sets of the closed-loop system. We show that we can compute these approximate reachable sets using semidefinite programming. We illustrate our method in a quadrotor example, in which we first approximate a nonlinear model predictive controller via a deep neural network and then apply our analysis tool to certify finite-time reachability and constraint satisfaction of the closed-loop system.

Computing the racing line using Bayesian optimization

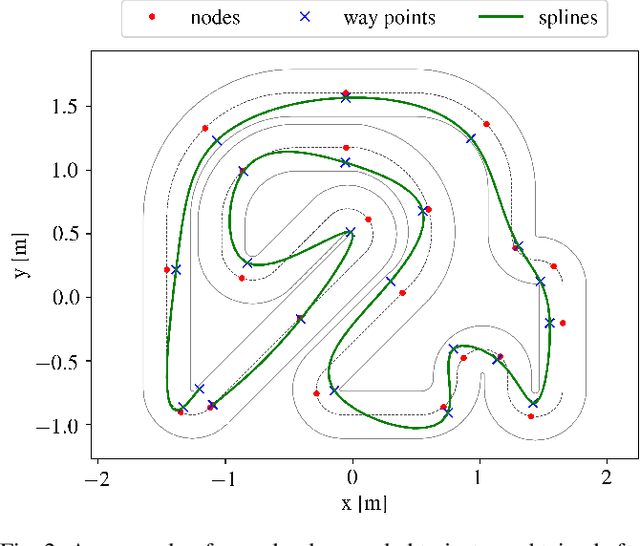
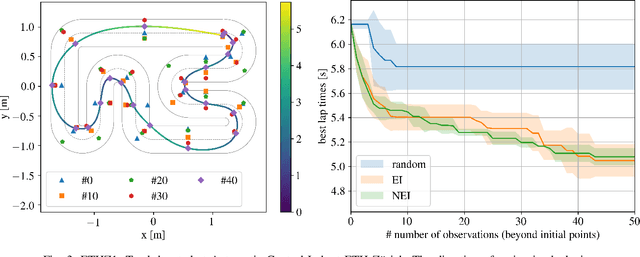
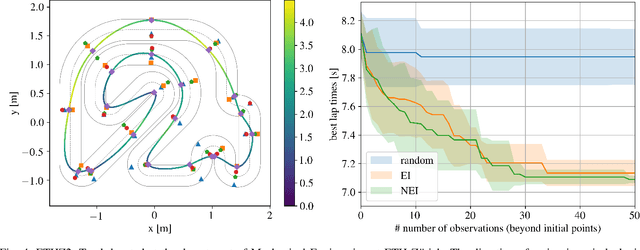
A good racing strategy and in particular the racing line is decisive to winning races in Formula 1, MotoGP, and other forms of motor racing. The racing line defines the path followed around a track as well as the optimal speed profile along the path. The objective is to minimize lap time by driving the vehicle at the limits of friction and handling capability. The solution naturally depends upon the geometry of the track and vehicle dynamics. We introduce a novel method to compute the racing line using Bayesian optimization. Our approach is fully data-driven and computationally more efficient compared to other methods based on dynamic programming and random search. The approach is specifically relevant in autonomous racing where teams can quickly compute the racing line for a new track and then exploit this information in the design of a motion planner and a controller to optimize real-time performance.

NeurOpt: Neural network based optimization for building energy management and climate control

Model predictive control (MPC) can provide significant energy cost savings in building operations in the form of energy-efficient control with better occupant comfort, lower peak demand charges, and risk-free participation in demand response. However, the engineering effort required to obtain physics-based models of buildings for MPC is considered to be the biggest bottleneck in making MPC scalable to real buildings. In this paper, we propose a data-driven control algorithm based on neural networks to reduce this cost of model identification. Our approach does not require building domain expertise or retrofitting of the existing heating and cooling systems. We validate our learning and control algorithms on a two-story building with 10 independently controlled zones, located in Italy. We learn dynamical models of energy consumption and zone temperatures with high accuracy and demonstrate energy savings and better occupant comfort compared to the default system controller.

Large Scale Model Predictive Control with Neural Networks and Primal Active Sets

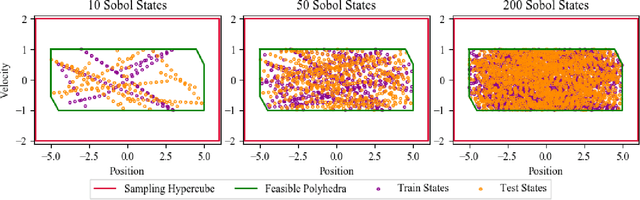
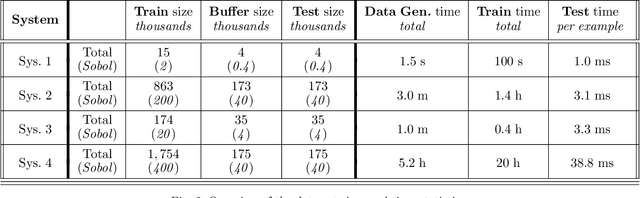
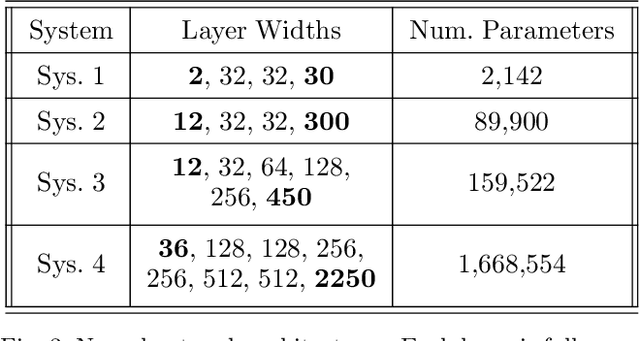
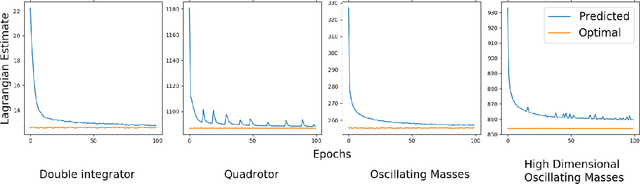
This work presents an explicit-implicit procedure that combines an offline trained neural network with an online primal active set solver to compute a model predictive control (MPC) law with guarantees on recursive feasibility and asymptotic stability. The neural network improves the suboptimality of the controller performance and accelerates online inference speed for large systems, while the primal active set method provides corrective steps to ensure feasibility and stability. We highlight the connections between MPC and neural networks and introduce a primal-dual loss function to train a neural network to initialize the online controller. We then demonstrate online computation of the primal feasibility and suboptimality criteria to provide the desired guarantees. Next, we use these neural network and criteria measures to accelerate an online primal active set method through warm starts and early termination. Finally, we present a data set generation algorithm that is critical for successfully applying our approach to high dimensional systems. The primary motivation is developing an algorithm that scales to systems that are challenging for current approaches, involving state and input dimensions as well as planning horizons in the order of tens to hundreds.