Lijie Chen
Diffusion Language Models are Provably Optimal Parallel Samplers
Dec 31, 2025Abstract:Diffusion language models (DLMs) have emerged as a promising alternative to autoregressive models for faster inference via parallel token generation. We provide a rigorous foundation for this advantage by formalizing a model of parallel sampling and showing that DLMs augmented with polynomial-length chain-of-thought (CoT) can simulate any parallel sampling algorithm using an optimal number of sequential steps. Consequently, whenever a target distribution can be generated using a small number of sequential steps, a DLM can be used to generate the distribution using the same number of optimal sequential steps. However, without the ability to modify previously revealed tokens, DLMs with CoT can still incur large intermediate footprints. We prove that enabling remasking (converting unmasked tokens to masks) or revision (converting unmasked tokens to other unmasked tokens) together with CoT further allows DLMs to simulate any parallel sampling algorithm with optimal space complexity. We further justify the advantage of revision by establishing a strict expressivity gap: DLMs with revision or remasking are strictly more expressive than those without. Our results not only provide a theoretical justification for the promise of DLMs as the most efficient parallel sampler, but also advocate for enabling revision in DLMs.
Understanding In-context Learning of Addition via Activation Subspaces
May 08, 2025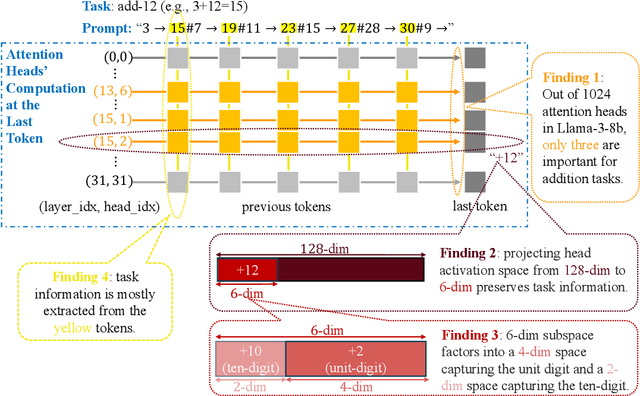
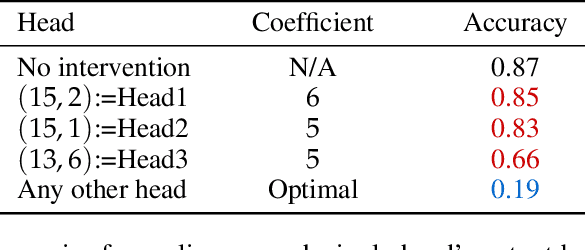
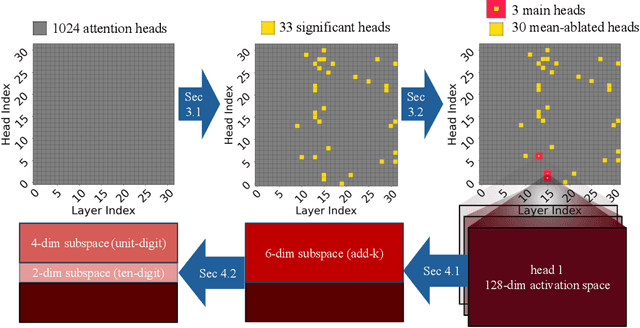
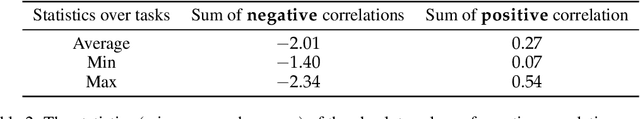
Abstract:To perform in-context learning, language models must extract signals from individual few-shot examples, aggregate these into a learned prediction rule, and then apply this rule to new examples. How is this implemented in the forward pass of modern transformer models? To study this, we consider a structured family of few-shot learning tasks for which the true prediction rule is to add an integer $k$ to the input. We find that Llama-3-8B attains high accuracy on this task for a range of $k$, and localize its few-shot ability to just three attention heads via a novel optimization approach. We further show the extracted signals lie in a six-dimensional subspace, where four of the dimensions track the unit digit and the other two dimensions track overall magnitude. We finally examine how these heads extract information from individual few-shot examples, identifying a self-correction mechanism in which mistakes from earlier examples are suppressed by later examples. Our results demonstrate how tracking low-dimensional subspaces across a forward pass can provide insight into fine-grained computational structures.
Why and How LLMs Hallucinate: Connecting the Dots with Subsequence Associations
Apr 17, 2025Abstract:Large language models (LLMs) frequently generate hallucinations-content that deviates from factual accuracy or provided context-posing challenges for diagnosis due to the complex interplay of underlying causes. This paper introduces a subsequence association framework to systematically trace and understand hallucinations. Our key insight is that hallucinations arise when dominant hallucinatory associations outweigh faithful ones. Through theoretical and empirical analyses, we demonstrate that decoder-only transformers effectively function as subsequence embedding models, with linear layers encoding input-output associations. We propose a tracing algorithm that identifies causal subsequences by analyzing hallucination probabilities across randomized input contexts. Experiments show our method outperforms standard attribution techniques in identifying hallucination causes and aligns with evidence from the model's training corpus. This work provides a unified perspective on hallucinations and a robust framework for their tracing and analysis.
LatentQA: Teaching LLMs to Decode Activations Into Natural Language
Dec 11, 2024Abstract:Interpretability methods seek to understand language model representations, yet the outputs of most such methods -- circuits, vectors, scalars -- are not immediately human-interpretable. In response, we introduce LatentQA, the task of answering open-ended questions about model activations in natural language. Towards solving LatentQA, we propose Latent Interpretation Tuning (LIT), which finetunes a decoder LLM on a dataset of activations and associated question-answer pairs, similar to how visual instruction tuning trains on question-answer pairs associated with images. We use the decoder for diverse reading applications, such as extracting relational knowledge from representations or uncovering system prompts governing model behavior. Our decoder also specifies a differentiable loss that we use to control models, such as debiasing models on stereotyped sentences and controlling the sentiment of generations. Finally, we extend LatentQA to reveal harmful model capabilities, such as generating recipes for bioweapons and code for hacking.
Theoretical limitations of multi-layer Transformer
Dec 04, 2024Abstract:Transformers, especially the decoder-only variants, are the backbone of most modern large language models; yet we do not have much understanding of their expressive power except for the simple $1$-layer case. Due to the difficulty of analyzing multi-layer models, all previous work relies on unproven complexity conjectures to show limitations for multi-layer Transformers. In this work, we prove the first $\textit{unconditional}$ lower bound against multi-layer decoder-only transformers. For any constant $L$, we prove that any $L$-layer decoder-only transformer needs a polynomial model dimension ($n^{\Omega(1)}$) to perform sequential composition of $L$ functions over an input of $n$ tokens. As a consequence, our results give: (1) the first depth-width trade-off for multi-layer transformers, exhibiting that the $L$-step composition task is exponentially harder for $L$-layer models compared to $(L+1)$-layer ones; (2) an unconditional separation between encoder and decoder, exhibiting a hard task for decoders that can be solved by an exponentially shallower and smaller encoder; (3) a provable advantage of chain-of-thought, exhibiting a task that becomes exponentially easier with chain-of-thought. On the technical side, we propose the multi-party $\textit{autoregressive}$ $\textit{communication}$ $\textit{model}$ that captures the computation of a decoder-only Transformer. We also introduce a new proof technique that finds a certain $\textit{indistinguishable}$ $\textit{decomposition}$ of all possible inputs iteratively for proving lower bounds in this model. We believe our new communication model and proof technique will be helpful to further understand the computational power of transformers.
On Distributed Differential Privacy and Counting Distinct Elements
Sep 21, 2020Abstract:We study the setup where each of $n$ users holds an element from a discrete set, and the goal is to count the number of distinct elements across all users, under the constraint of $(\epsilon, \delta)$-differentially privacy: - In the non-interactive local setting, we prove that the additive error of any protocol is $\Omega(n)$ for any constant $\epsilon$ and for any $\delta$ inverse polynomial in $n$. - In the single-message shuffle setting, we prove a lower bound of $\Omega(n)$ on the error for any constant $\epsilon$ and for some $\delta$ inverse quasi-polynomial in $n$. We do so by building on the moment-matching method from the literature on distribution estimation. - In the multi-message shuffle setting, we give a protocol with at most one message per user in expectation and with an error of $\tilde{O}(\sqrt(n))$ for any constant $\epsilon$ and for any $\delta$ inverse polynomial in $n$. Our protocol is also robustly shuffle private, and our error of $\sqrt(n)$ matches a known lower bound for such protocols. Our proof technique relies on a new notion, that we call dominated protocols, and which can also be used to obtain the first non-trivial lower bounds against multi-message shuffle protocols for the well-studied problems of selection and learning parity. Our first lower bound for estimating the number of distinct elements provides the first $\omega(\sqrt(n))$ separation between global sensitivity and error in local differential privacy, thus answering an open question of Vadhan (2017). We also provide a simple construction that gives $\tilde{\Omega}(n)$ separation between global sensitivity and error in two-party differential privacy, thereby answering an open question of McGregor et al. (2011).
Nearly Optimal Sampling Algorithms for Combinatorial Pure Exploration
Jun 04, 2017Abstract:We study the combinatorial pure exploration problem Best-Set in stochastic multi-armed bandits. In a Best-Set instance, we are given $n$ arms with unknown reward distributions, as well as a family $\mathcal{F}$ of feasible subsets over the arms. Our goal is to identify the feasible subset in $\mathcal{F}$ with the maximum total mean using as few samples as possible. The problem generalizes the classical best arm identification problem and the top-$k$ arm identification problem, both of which have attracted significant attention in recent years. We provide a novel instance-wise lower bound for the sample complexity of the problem, as well as a nontrivial sampling algorithm, matching the lower bound up to a factor of $\ln|\mathcal{F}|$. For an important class of combinatorial families, we also provide polynomial time implementation of the sampling algorithm, using the equivalence of separation and optimization for convex program, and approximate Pareto curves in multi-objective optimization. We also show that the $\ln|\mathcal{F}|$ factor is inevitable in general through a nontrivial lower bound construction. Our results significantly improve several previous results for several important combinatorial constraints, and provide a tighter understanding of the general Best-Set problem. We further introduce an even more general problem, formulated in geometric terms. We are given $n$ Gaussian arms with unknown means and unit variance. Consider the $n$-dimensional Euclidean space $\mathbb{R}^n$, and a collection $\mathcal{O}$ of disjoint subsets. Our goal is to determine the subset in $\mathcal{O}$ that contains the $n$-dimensional vector of the means. The problem generalizes most pure exploration bandit problems studied in the literature. We provide the first nearly optimal sample complexity upper and lower bounds for the problem.
Towards Instance Optimal Bounds for Best Arm Identification
May 24, 2017Abstract:In the classical best arm identification (Best-$1$-Arm) problem, we are given $n$ stochastic bandit arms, each associated with a reward distribution with an unknown mean. We would like to identify the arm with the largest mean with probability at least $1-\delta$, using as few samples as possible. Understanding the sample complexity of Best-$1$-Arm has attracted significant attention since the last decade. However, the exact sample complexity of the problem is still unknown. Recently, Chen and Li made the gap-entropy conjecture concerning the instance sample complexity of Best-$1$-Arm. Given an instance $I$, let $\mu_{[i]}$ be the $i$th largest mean and $\Delta_{[i]}=\mu_{[1]}-\mu_{[i]}$ be the corresponding gap. $H(I)=\sum_{i=2}^n\Delta_{[i]}^{-2}$ is the complexity of the instance. The gap-entropy conjecture states that $\Omega\left(H(I)\cdot\left(\ln\delta^{-1}+\mathsf{Ent}(I)\right)\right)$ is an instance lower bound, where $\mathsf{Ent}(I)$ is an entropy-like term determined by the gaps, and there is a $\delta$-correct algorithm for Best-$1$-Arm with sample complexity $O\left(H(I)\cdot\left(\ln\delta^{-1}+\mathsf{Ent}(I)\right)+\Delta_{[2]}^{-2}\ln\ln\Delta_{[2]}^{-1}\right)$. If the conjecture is true, we would have a complete understanding of the instance-wise sample complexity of Best-$1$-Arm. We make significant progress towards the resolution of the gap-entropy conjecture. For the upper bound, we provide a highly nontrivial algorithm which requires \[O\left(H(I)\cdot\left(\ln\delta^{-1} +\mathsf{Ent}(I)\right)+\Delta_{[2]}^{-2}\ln\ln\Delta_{[2]}^{-1}\mathrm{polylog}(n,\delta^{-1})\right)\] samples in expectation. For the lower bound, we show that for any Gaussian Best-$1$-Arm instance with gaps of the form $2^{-k}$, any $\delta$-correct monotone algorithm requires $\Omega\left(H(I)\cdot\left(\ln\delta^{-1} + \mathsf{Ent}(I)\right)\right)$ samples in expectation.
Nearly Instance Optimal Sample Complexity Bounds for Top-k Arm Selection
Feb 13, 2017

Abstract:In the Best-$k$-Arm problem, we are given $n$ stochastic bandit arms, each associated with an unknown reward distribution. We are required to identify the $k$ arms with the largest means by taking as few samples as possible. In this paper, we make progress towards a complete characterization of the instance-wise sample complexity bounds for the Best-$k$-Arm problem. On the lower bound side, we obtain a novel complexity term to measure the sample complexity that every Best-$k$-Arm instance requires. This is derived by an interesting and nontrivial reduction from the Best-$1$-Arm problem. We also provide an elimination-based algorithm that matches the instance-wise lower bound within doubly-logarithmic factors. The sample complexity of our algorithm strictly dominates the state-of-the-art for Best-$k$-Arm (module constant factors).
On the Optimal Sample Complexity for Best Arm Identification
Aug 23, 2016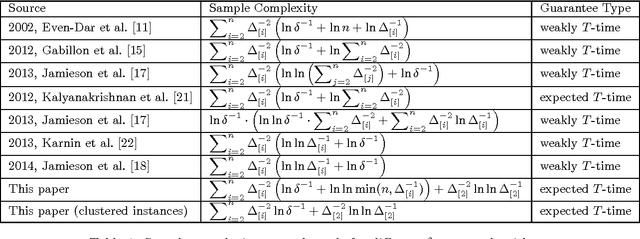
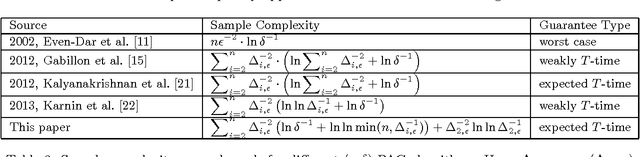
Abstract:We study the best arm identification (BEST-1-ARM) problem, which is defined as follows. We are given $n$ stochastic bandit arms. The $i$th arm has a reward distribution $D_i$ with an unknown mean $\mu_{i}$. Upon each play of the $i$th arm, we can get a reward, sampled i.i.d. from $D_i$. We would like to identify the arm with the largest mean with probability at least $1-\delta$, using as few samples as possible. We provide a nontrivial algorithm for BEST-1-ARM, which improves upon several prior upper bounds on the same problem. We also study an important special case where there are only two arms, which we call the sign problem. We provide a new lower bound of sign, simplifying and significantly extending a classical result by Farrell in 1964, with a completely new proof. Using the new lower bound for sign, we obtain the first lower bound for BEST-1-ARM that goes beyond the classic Mannor-Tsitsiklis lower bound, by an interesting reduction from Sign to BEST-1-ARM. We propose an interesting conjecture concerning the optimal sample complexity of BEST-1-ARM from the perspective of instance-wise optimality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge