Fast Heavy Inner Product Identification Between Weights and Inputs in Neural Network Training

In this paper, we consider a heavy inner product identification problem, which generalizes the Light Bulb problem~(\cite{prr89}): Given two sets $A \subset \{-1,+1\}^d$ and $B \subset \{-1,+1\}^d$ with $|A|=|B| = n$, if there are exact $k$ pairs whose inner product passes a certain threshold, i.e., $\{(a_1, b_1), \cdots, (a_k, b_k)\} \subset A \times B$ such that $\forall i \in [k], \langle a_i,b_i \rangle \geq \rho \cdot d$, for a threshold $\rho \in (0,1)$, the goal is to identify those $k$ heavy inner products. We provide an algorithm that runs in $O(n^{2 \omega / 3+ o(1)})$ time to find the $k$ inner product pairs that surpass $\rho \cdot d$ threshold with high probability, where $\omega$ is the current matrix multiplication exponent. By solving this problem, our method speed up the training of neural networks with ReLU activation function.

GPT-4V as a Generalist Evaluator for Vision-Language Tasks

Automatically evaluating vision-language tasks is challenging, especially when it comes to reflecting human judgments due to limitations in accounting for fine-grained details. Although GPT-4V has shown promising results in various multi-modal tasks, leveraging GPT-4V as a generalist evaluator for these tasks has not yet been systematically explored. We comprehensively validate GPT-4V's capabilities for evaluation purposes, addressing tasks ranging from foundational image-to-text and text-to-image synthesis to high-level image-to-image translations and multi-images to text alignment. We employ two evaluation methods, single-answer grading and pairwise comparison, using GPT-4V. Notably, GPT-4V shows promising agreement with humans across various tasks and evaluation methods, demonstrating immense potential for multi-modal LLMs as evaluators. Despite limitations like restricted visual clarity grading and real-world complex reasoning, its ability to provide human-aligned scores enriched with detailed explanations is promising for universal automatic evaluator.

Is Solving Graph Neural Tangent Kernel Equivalent to Training Graph Neural Network?

A rising trend in theoretical deep learning is to understand why deep learning works through Neural Tangent Kernel (NTK) [jgh18], a kernel method that is equivalent to using gradient descent to train a multi-layer infinitely-wide neural network. NTK is a major step forward in the theoretical deep learning because it allows researchers to use traditional mathematical tools to analyze properties of deep neural networks and to explain various neural network techniques from a theoretical view. A natural extension of NTK on graph learning is \textit{Graph Neural Tangent Kernel (GNTK)}, and researchers have already provide GNTK formulation for graph-level regression and show empirically that this kernel method can achieve similar accuracy as GNNs on various bioinformatics datasets [dhs+19]. The remaining question now is whether solving GNTK regression is equivalent to training an infinite-wide multi-layer GNN using gradient descent. In this paper, we provide three new theoretical results. First, we formally prove this equivalence for graph-level regression. Second, we present the first GNTK formulation for node-level regression. Finally, we prove the equivalence for node-level regression.

Online Adaptive Mahalanobis Distance Estimation

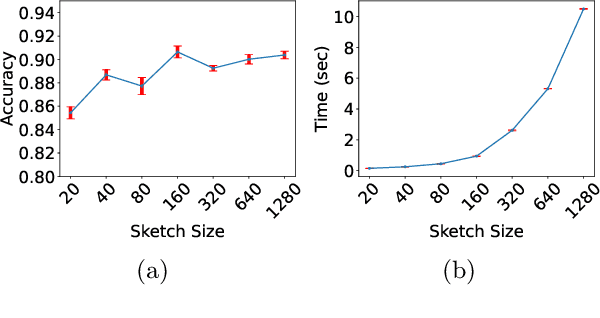
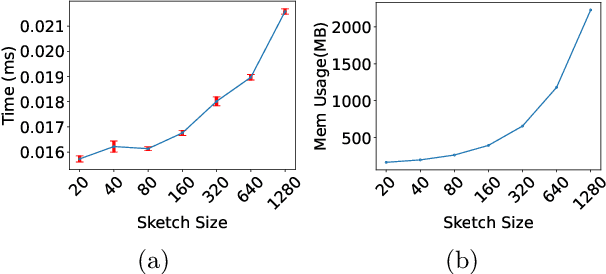
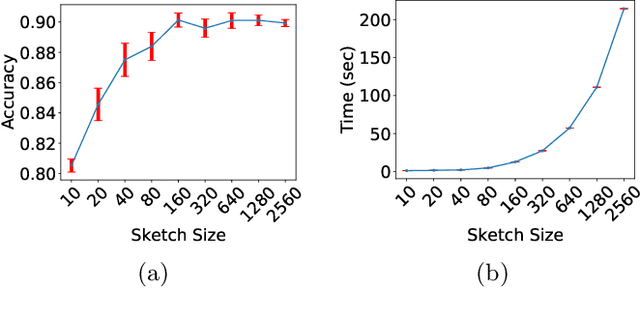
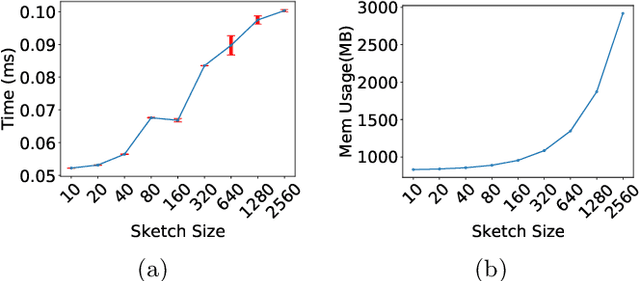
Mahalanobis metrics are widely used in machine learning in conjunction with methods like $k$-nearest neighbors, $k$-means clustering, and $k$-medians clustering. Despite their importance, there has not been any prior work on applying sketching techniques to speed up algorithms for Mahalanobis metrics. In this paper, we initiate the study of dimension reduction for Mahalanobis metrics. In particular, we provide efficient data structures for solving the Approximate Distance Estimation (ADE) problem for Mahalanobis distances. We first provide a randomized Monte Carlo data structure. Then, we show how we can adapt it to provide our main data structure which can handle sequences of \textit{adaptive} queries and also online updates to both the Mahalanobis metric matrix and the data points, making it amenable to be used in conjunction with prior algorithms for online learning of Mahalanobis metrics.

Efficient SGD Neural Network Training via Sublinear Activated Neuron Identification

Deep learning has been widely used in many fields, but the model training process usually consumes massive computational resources and time. Therefore, designing an efficient neural network training method with a provable convergence guarantee is a fundamental and important research question. In this paper, we present a static half-space report data structure that consists of a fully connected two-layer neural network for shifted ReLU activation to enable activated neuron identification in sublinear time via geometric search. We also prove that our algorithm can converge in $O(M^2/\epsilon^2)$ time with network size quadratic in the coefficient norm upper bound $M$ and error term $\epsilon$.

Fast Submodular Function Maximization

Submodular functions have many real-world applications, such as document summarization, sensor placement, and image segmentation. For all these applications, the key building block is how to compute the maximum value of a submodular function efficiently. We consider both the online and offline versions of the problem: in each iteration, the data set changes incrementally or is not changed, and a user can issue a query to maximize the function on a given subset of the data. The user can be malicious, issuing queries based on previous query results to break the competitive ratio for the online algorithm. Today, the best-known algorithm for online submodular function maximization has a running time of $O(n k d^2)$ where $n$ is the total number of elements, $d$ is the feature dimension and $k$ is the number of elements to be selected. We propose a new method based on a novel search tree data structure. Our algorithm only takes $\widetilde{O}(nk + kd^2 + nd)$ time.

A General Algorithm for Solving Rank-one Matrix Sensing

Matrix sensing has many real-world applications in science and engineering, such as system control, distance embedding, and computer vision. The goal of matrix sensing is to recover a matrix $A_\star \in \mathbb{R}^{n \times n}$, based on a sequence of measurements $(u_i,b_i) \in \mathbb{R}^{n} \times \mathbb{R}$ such that $u_i^\top A_\star u_i = b_i$. Previous work [ZJD15] focused on the scenario where matrix $A_{\star}$ has a small rank, e.g. rank-$k$. Their analysis heavily relies on the RIP assumption, making it unclear how to generalize to high-rank matrices. In this paper, we relax that rank-$k$ assumption and solve a much more general matrix sensing problem. Given an accuracy parameter $\delta \in (0,1)$, we can compute $A \in \mathbb{R}^{n \times n}$ in $\widetilde{O}(m^{3/2} n^2 \delta^{-1} )$, such that $ |u_i^\top A u_i - b_i| \leq \delta$ for all $i \in [m]$. We design an efficient algorithm with provable convergence guarantees using stochastic gradient descent for this problem.

Adaptive and Dynamic Multi-Resolution Hashing for Pairwise Summations

In this paper, we propose Adam-Hash: an adaptive and dynamic multi-resolution hashing data-structure for fast pairwise summation estimation. Given a data-set $X \subset \mathbb{R}^d$, a binary function $f:\mathbb{R}^d\times \mathbb{R}^d\to \mathbb{R}$, and a point $y \in \mathbb{R}^d$, the Pairwise Summation Estimate $\mathrm{PSE}_X(y) := \frac{1}{|X|} \sum_{x \in X} f(x,y)$. For any given data-set $X$, we need to design a data-structure such that given any query point $y \in \mathbb{R}^d$, the data-structure approximately estimates $\mathrm{PSE}_X(y)$ in time that is sub-linear in $|X|$. Prior works on this problem have focused exclusively on the case where the data-set is static, and the queries are independent. In this paper, we design a hashing-based PSE data-structure which works for the more practical \textit{dynamic} setting in which insertions, deletions, and replacements of points are allowed. Moreover, our proposed Adam-Hash is also robust to adaptive PSE queries, where an adversary can choose query $q_j \in \mathbb{R}^d$ depending on the output from previous queries $q_1, q_2, \dots, q_{j-1}$.

A Sublinear Adversarial Training Algorithm

Adversarial training is a widely used strategy for making neural networks resistant to adversarial perturbations. For a neural network of width $m$, $n$ input training data in $d$ dimension, it takes $\Omega(mnd)$ time cost per training iteration for the forward and backward computation. In this paper we analyze the convergence guarantee of adversarial training procedure on a two-layer neural network with shifted ReLU activation, and shows that only $o(m)$ neurons will be activated for each input data per iteration. Furthermore, we develop an algorithm for adversarial training with time cost $o(m n d)$ per iteration by applying half-space reporting data structure.